目标
· SVM其实也是做二分类的,可是和感知机、逻辑回归不同的是,SVM希望找到最优解。
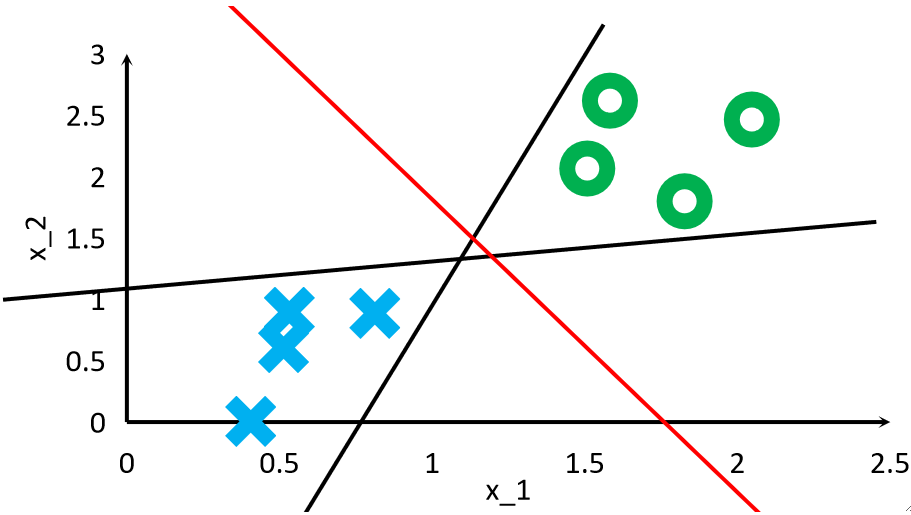
· 可以看到,三条线都可以把训练集分开,但是红色线是最好的,因为可以容纳的误差最大,SVM就希望找到这条红色线。
最大间隔问题(Max Margin Problem)
· 既然是做二分类,那我们的模型和感知机、逻辑回归一样,是一个线性模型:
· 同理,我们的决策面就是:
· 值得注意的是,我们在学习感知机的时候提到过,给模型两边乘一个\lambda,不会影响决策面。只是改变了倾斜角度。
支持向量 (Support Vector)
· 找到离我们画出的分割线最近的两个点(一般一堆一个,但也可以一堆两个),这两个点就是支持向量:
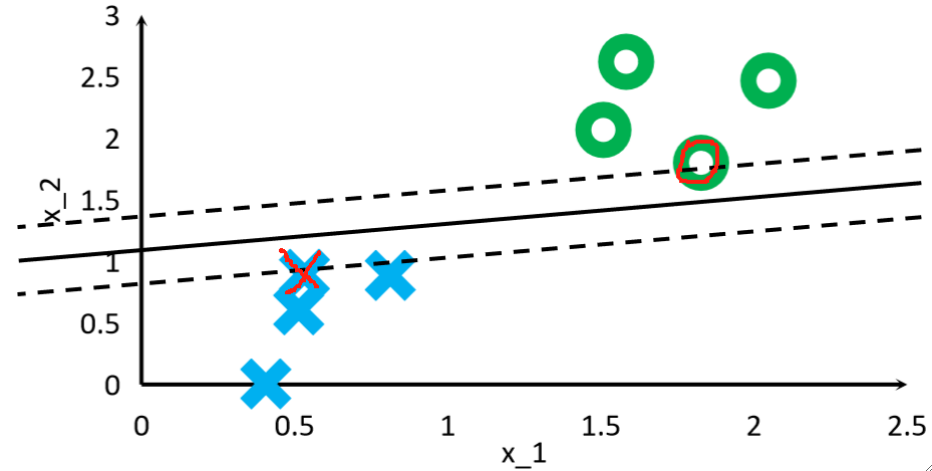
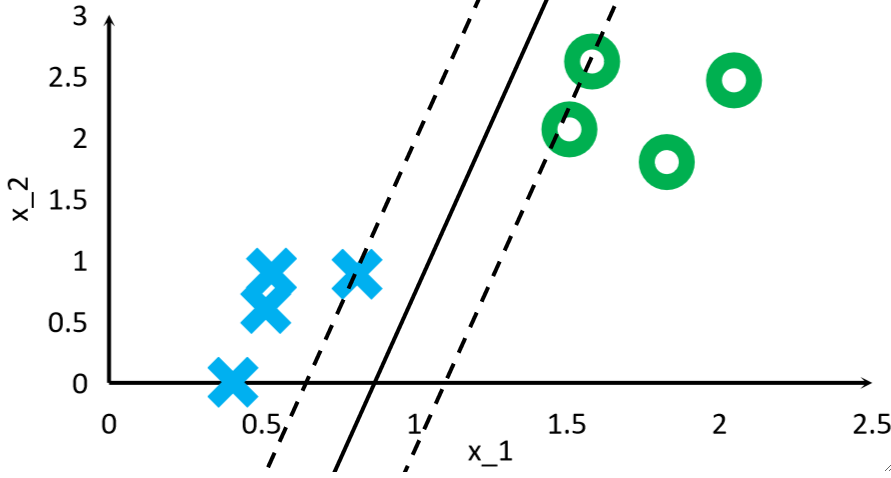
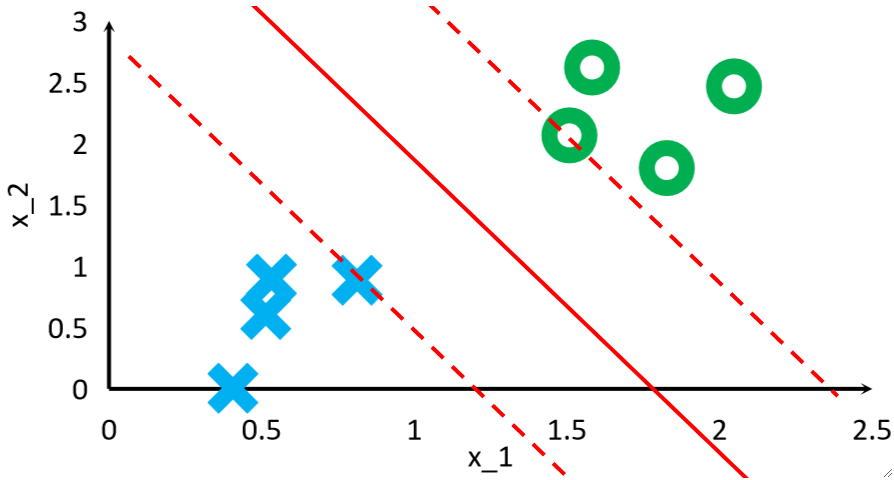
· 可以看到,根据我们画出的分割线的位置不同,找到的支持向量也不同。
· 找到了支持向量之后,我们的目标其实就不是找那条分割线在哪里了,而是最大化支持向量间的距离!
· 最大化支持向量间的距离后,我们取中间的那条线就可以了。
· 由此可见,支持向量的样本x代入y^{(i)}(w^Tx^{(i)}+b=c)计算点到决策面的“距离”得到c,而所有非支持向量代入计算都大于c。
· 然后,我们给决策面两边同时乘一个1/c,这样w就变成了w/c,b就变成了b/c,但是决策面不受影响:
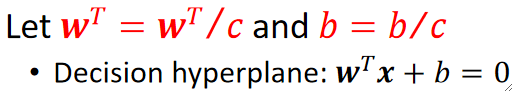
· 乘完1/c之后,原本计算点到决策面的“距离”就从c变为了1了,这样做的好处是简便计算:
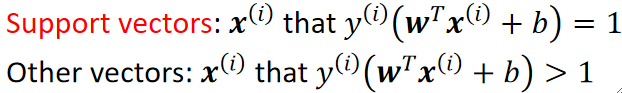
· 这样,我们计算支持向量真正的点到决策面的距离就变为了1/||w||,这样计算量就降低了很多:
· 这样,两个支持向量到决策面的总距离为\frac{2}{||\textbf{w}||},也就是说,我们现在要做的就是最大化这个值就可以了。
· 现在我们的问题就变成了如何让这个总距离最大,我们把这个问题就称为最大间隔问题,同时,我们限制每个点的“距离”大于等于1:
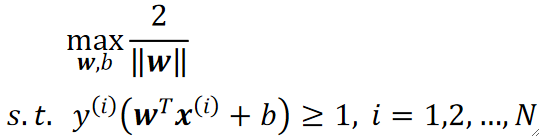
· 这个限制条件是为了防止最终的决策面离某一堆太近,这样的效果就比较差。
· 从最优化理论我们可以知道,求\frac{2}{||\textbf{w}||}的最大值其实就是求\frac{||\textbf{w}||}{2}的最小值。
· 求\frac{2}{||\textbf{w}||}的最小值,因为||\textbf{w}||=\sqrt{w_1^2+w_2^2+...},所以其实就是求\frac{||\textbf{w}||^2}{2}的最小值,少算一个根号,又因为\frac{||\textbf{w}||^2}{2}=\frac{\textbf{w}^T\textbf{w}}{2},再对限制条件移项,所以最终我们要求的就变成了:
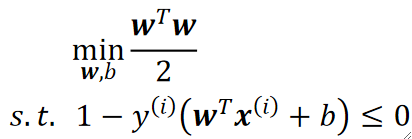
拉格朗日乘子法(等式约束下)
· 为了求上面式子的最小值,我们需要引入拉格朗日乘子法,但是上面的是不等式约束,为了简单先入个门,我们从等式约束开始。
· 定义如下:
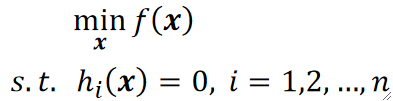
· 拉格朗日乘子法所做的,就是把限制条件放到等式里面,即:
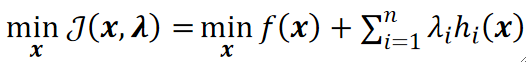
· 为什么可以这么做?因为限制条件h_i(x)=0,这样无论加多少个也不影响。
· 这样我们只需要求J的最小值就可以了,就是对对应的参数求偏导,注意我们引入了\lambda:
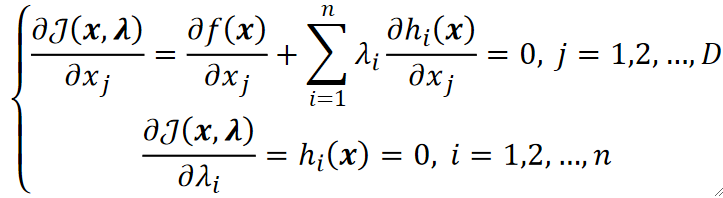
· 这里假设我们要求的f(x)为\frac{x_1^2+x_2^2}{2},限制条件h(x)只有一个,下图的蓝色为f(x)的图像,黄色线为限制条件:
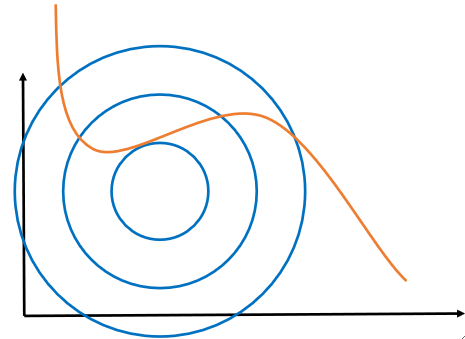
· 由求偏导的第一个式子,把h(x)那一项移过去右边之后,我们可以得到f(x)的梯度和h(x)的梯度的关系,套入我们的例子就是:
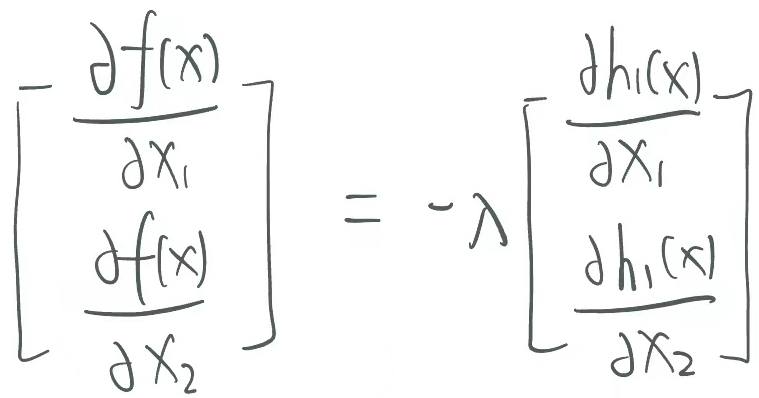
· 这两个都是向量,所以我们可以理解为f(x)的梯度和h(x)的梯度应该共线。
· 既然是这样的话,我们在图上找,就只能找到f(x)和h(x)的切点满足条件,即:
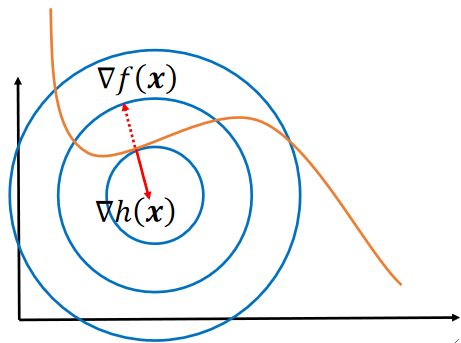
· 如果限制条件不止一个了,其实也是一样的:
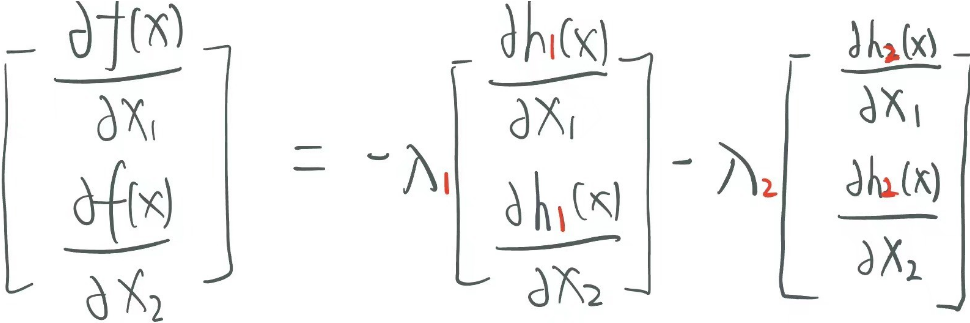
· 这样在图上找就只有三线的交点了,即h1和h2的梯度通过平行四边形法则加法后与f的梯度共线:
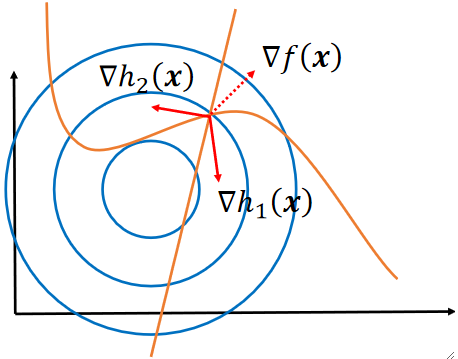
· 然后联立方程就可以解出x1,x2,\lambda的值。
拉格朗日乘子法(不等式约束下)
原问题(Primal Problem)
· 回到我们的问题,我们需要解决的是不等式约束下的最小值,即:
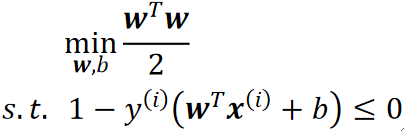
· 思想其实跟等式约束下的差不多,就是把限制条件加到式子里,不过此时,我们要求的就是一个最小最大问题了:
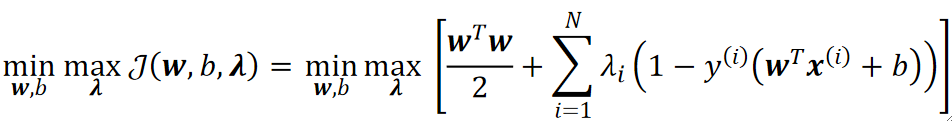
· 可以看到,我们就是先固定一个w,b,然后对于每个\lambda,我们需要计算出最大的那一个,最后去最小的w,b。其实跟两层循环是一样的。
· 值得注意的是,现在限制条件h(x)不再是0了,因此我们需要给\lambda规定一个范围,至于为什么,后面会讲:
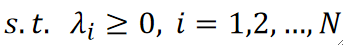
· 对于上面这个求最大最小,我们给它一个名字——原问题。
· 现在我们要分析一下,我们上面写的原问题,和我们要求的问题真的是等价的么?

· 我们先来看内层循环,既然限制条件已经通过拉格朗日乘子法放到式子里面去了,那我怎么取其实都无所谓,我们来分析一下:
如果限制条件满足,根据限制条件\lambda >= 0,此时\lambda只能为0,否则这一项会越来越小,这样就与我们想取max背道而驰了。
这样子内层循环得到的最大值就是wTw/2:
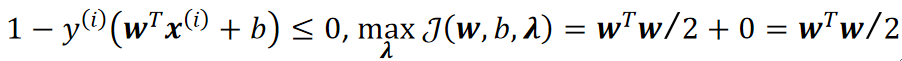
如果限制条件不满足,这样\lambda>=0,后面也大于0,这样就可以无限大下去:
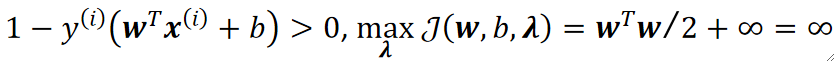
· 然后看外层循环,要去小的那一个,很明显wTw/2比无穷小:

· 可以发现,最后推出来原问题的结果跟我们要求的一模一样,限制条件也没变,因为无穷的情况直接被我们排除了。
· 现在我们知道为什么要限制\lambda>=0了,如果没有这个条件,两种结果都可能得到无穷了,因为\lambda可以取负无穷了,这样就把我们的结果改变了。
· 但是在原问题里面去解w和b是很困难的,因此我们要把原问题转化为对偶问题去解。
对偶问题(Dual Problem)
· 我们的原问题是解最大最小问题,对偶问题就是把顺序换一下,求最小最大问题:

· 换完之后能保证对偶问题和原问题是一样的吗?很遗憾,不完全能,但问题不大。
· 它们满足的是原问题的解大于等于对偶问题的解:
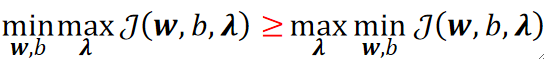
· 幸运的是,对于SVM的最大间隔问题,它是满足对偶问题的解等于对偶问题的解的。
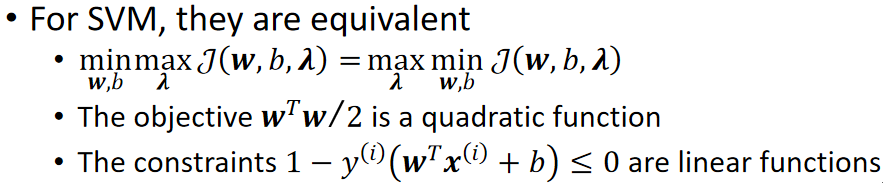
· 至于为什么,请参考《最优化理论》这门课。
使用拉格朗日乘子法解决对偶问题
· 回忆一下我们的艰苦之路,首先要求f(x)的最小值,然后转化为原问题,然后转化为对偶问题。
· 因为对于SVM的最大间隔问题,原问题的解等于对偶问题,因此我们称其为强对偶(Strong Duality):
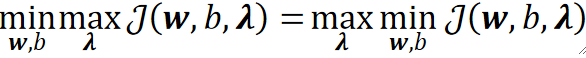
· 数学家们证明了,如果强对偶存在的话,那么该问题必满足KKT条件(Karush-Kuhn-Tucker Conditions)。
· 其实KKT条件跟我们等式约束下的拉格朗日乘子法很像:
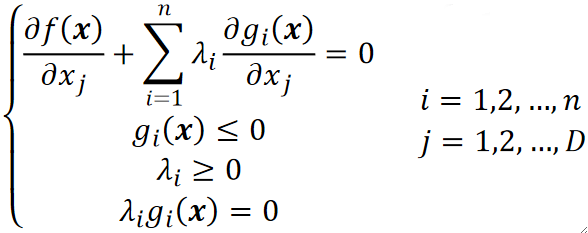
· 第一项跟等式约束下的一样;第二项差不多,是限制条件;第三项是\lambda的限制,前面推过;第四项必满足,后面会推。
在一个限制条件的情况下,如果可行域包含了最优点,根据计算可以发现,此时g(x)<0,f的梯度为0,而g的梯度不为0,那么此时\lambda必须为0:
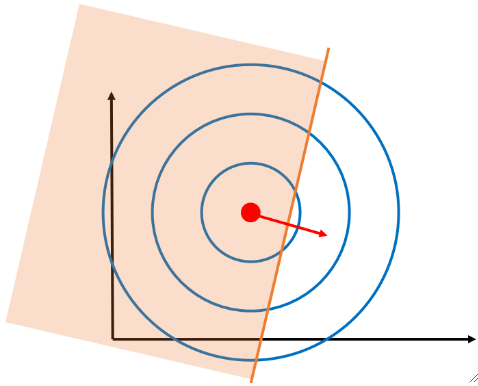
在一个限制条件的情况下,如果可行域不包含最优点,此时g(x)=0,f和g的梯度都不为0,那么和之前一样,只能找共线的时候的情况,很明显,就是切线的时候,两个梯度才能平行:
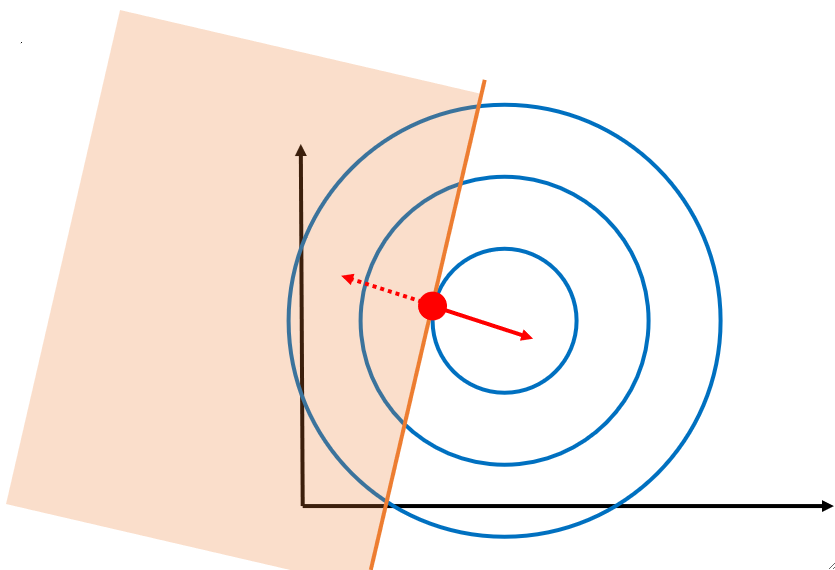
值得注意的是,这种情况下,\lambda是不可以为0的,否则等式右边就是0了,此时\lambda必须要大于0。但是没关系,因为此时最优点在限制条件的线上,所以g(x)=0,这样就能推出我们KKT的第四个条件,即\lambda_i g_i(x)=0。
通过上面的两个例子,我们可以把限制条件分为松弛的限制条件和紧致的限制条件。
1. 松弛的限制条件,就是像第一种一样,不会影响最优点的位置。在这种情况下,\lambda必定为0,g(x)<0。
2. 紧致的限制条件,就是像第二种一样,把最优点“强行拉过去”,会影响最优点的位置。在这种情况下,\lambda必定>0,g(x)=0。
3. 我们可以发现,只有当样本点是支持向量的时候,g(x)=0,当样本点是非支持向量的时候,g(x)<0。
我们把KKT的第四个条件,即\lambda_i g_i(x)=0称为互补松弛条件(Complementary Slackness)。
我们用互补松弛条件来判断一下下面的情况,有两个限制条件,此时很明显这两个限制条件都是紧致的,那么我们可以直接断定g_1(x)=0,g_2(x)=0。
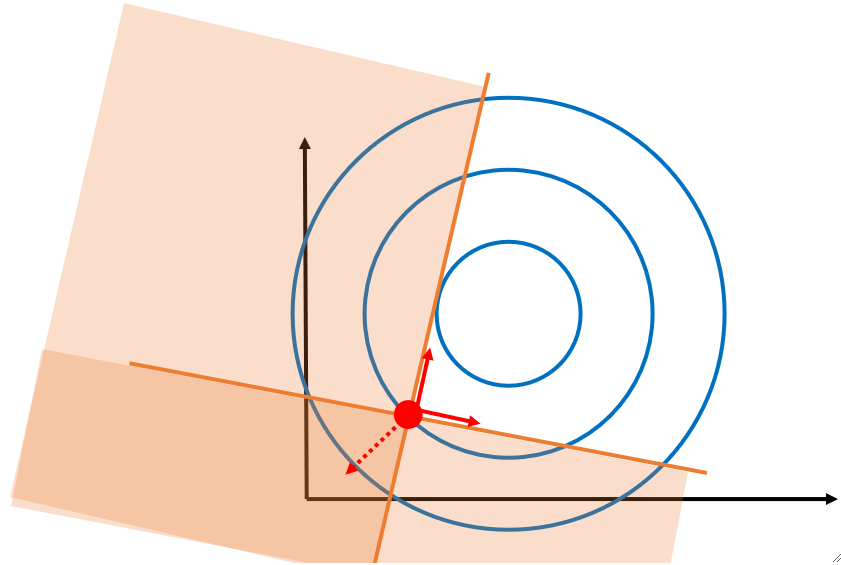
再举个例子,下面的情况有三个限制条件,可以看到g1和g2是紧致的,g3是松弛的,故g_1(x)=0,g_2(x)=0,g_3(x)<0。
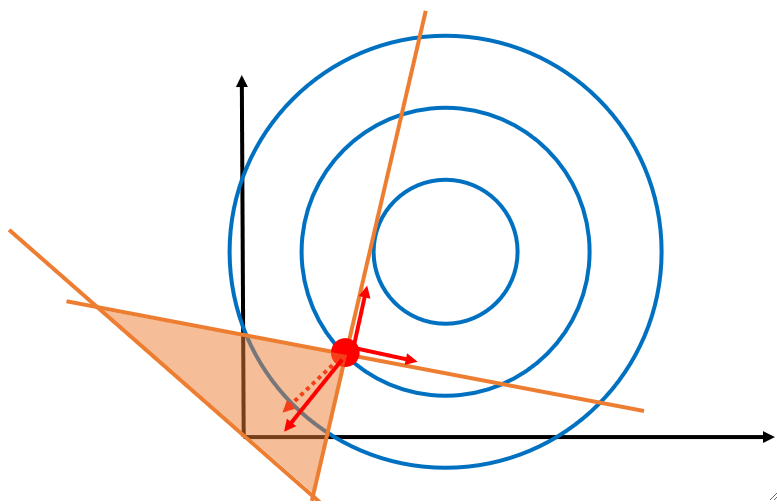
可以发现。g3给到的向量是多余的,不但没有作出贡献还拖后腿了,因此,所有松弛的限制条件都是多余的。
· 现在,所有的理论基础已经打好,终于可以开始解我们的对偶问题了!
· 回忆一下,我们要解决的问题是:
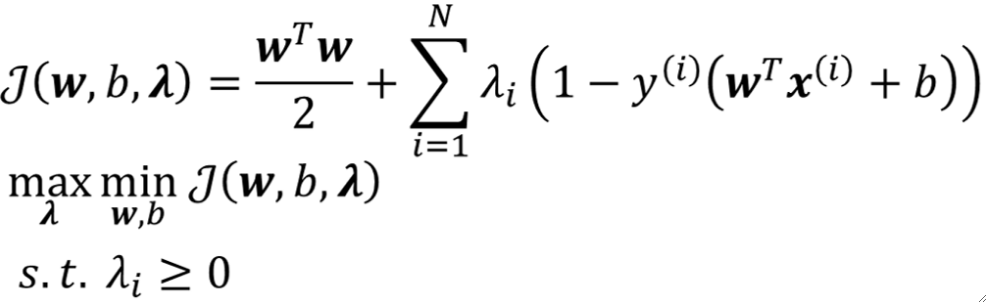
· 首先,我们先来解决内层循环,即min的部分。
· 在解min的部分的时候\lambda是固定的,因此我们可以把它当做一个常数,然后求偏导并令为0有:
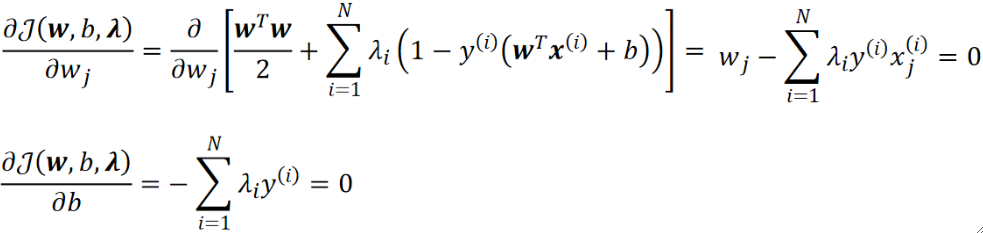
· 为了后续方便,我们把对w的偏导进行一个移项,并把它写成向量的形式:
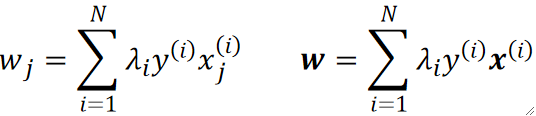
· 然后我们把所有的标签y和样本x都代入就可以算出所有的w。
· 然后我们还需要解出b,根据我们的模型y^{(i)}(w^Tx^{(i)}+b),我们随便挑一个样本点带进去就可以算出b:
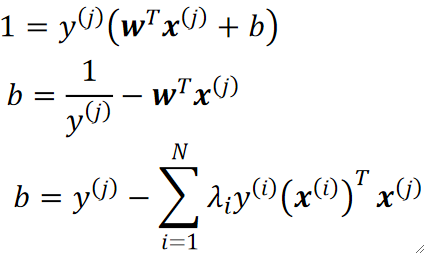
· 还没有结束哦!w和b的解里面现在都带着一个\lambda,这是需要去外层循环才能解出来的。
· 首先我们把求出来的w代入J,计算思路如下:

· 然后,我们把求J的最大值转换为求最小值,其实就是加个负号的事:
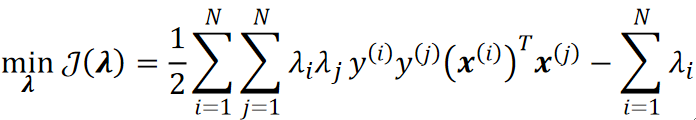
· 然后我们就可以手算得出\lambda了。
· 如果要编程,则需要学习序列最小化算法(Sequential Minimal optimization,SMO)。
· 至此,w和b都能完全算出来了。
手算SVM
· 给出三个点x^{(1)} = [3,3]^T, x^{(2)} = [4,3]^T, x^{(3)} = [1,1] ,其中x1和x2是一类,x3是另一类,计算一个SVM决策面。
· 首先,根据公式,我们把所有点都带进去:
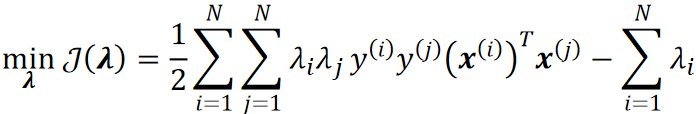
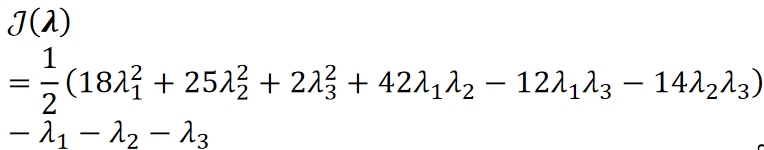
· 然后根据公式,把所有标签代入,可以得到关于\lambda的式子:
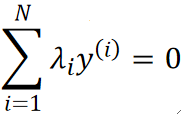
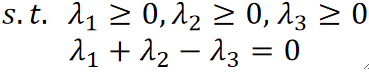
· 然后,我们选择两个点作为支持向量:
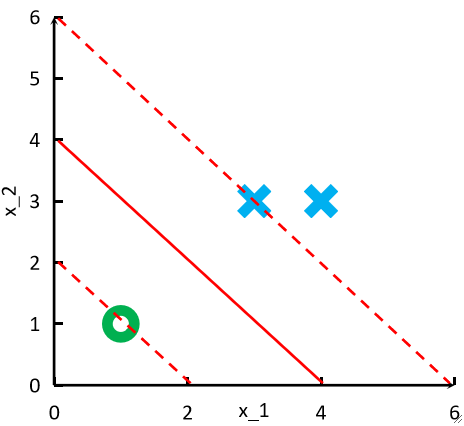
· 这样根据互补松弛条件就可以知道\lambda_1和\lambda_3是>0,\lambda_2=0。
· 然后我们代入J的式子就有:
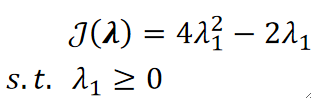
· 然后根据二次函数,求得当\lambda_1=1/4的时候得到最小。
· 这样\lambda_1=\lambda_3=1/4,\lambda_2=0。
· 然后我们带入算w和b的公式就有:
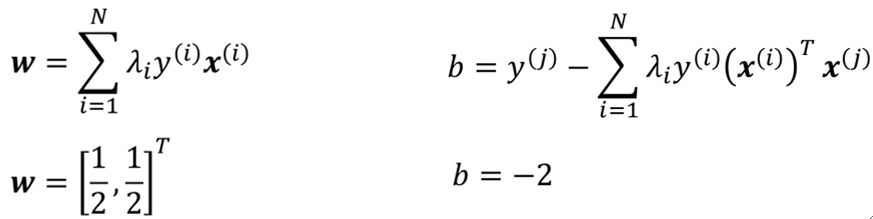
· 最后就可以得到我们的超平面:
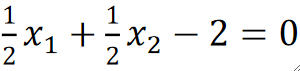
核技巧(Kernel Trick)
· SVM能做的事情其实只是能分线性可分的数据,如果数据不是线性可分的,那SVM的效果就会非常差:
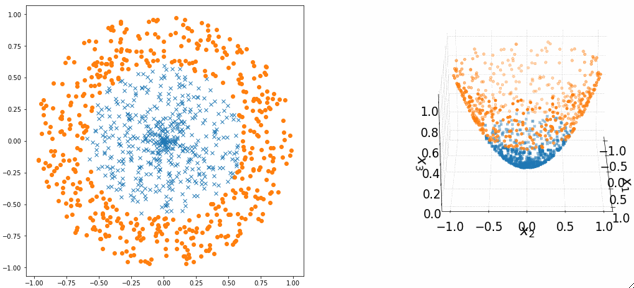
· 核技巧做了什么呢?看下面的例子。
· 我们给原来的线性模型引入一个新的维度,但是这个维度是通过x1和x2算出来的:
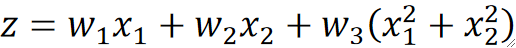
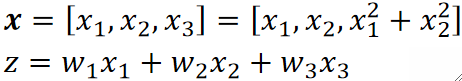
· 这样子其实本质上我们的模型还是一个线性模型。SVM又能做了!
· 从上图中可以看到,在三维空间中,两组数据就可以线性可分的了!
· 所以核技巧的核心思想就是扩展维度,把低维的样本映射到高维去。
· 有一个结论,当我们把样本映射的维度越高,那映射后的结果就越有可能线性可分。
· 因此,理论上我们能把x映射到无穷维,这样映射之后就必然可分。
· 我们用\phi(x)表示把x映射到更高维的空间去,那么模型就从z=w^Tx+b变为了=w^T\phi(x)+b,同时w和x也升到了更高维度。
· 有趣的一点是,对于模型中的w、x、b,我们都不需要知道,就可以算出z来。
· 首先,我们把之前推导出来的计算w和b的式子,换成\phi(x)的形态:
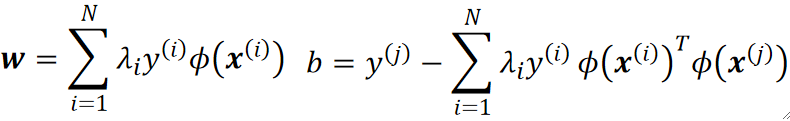
· 然后把这两个往模型里代:
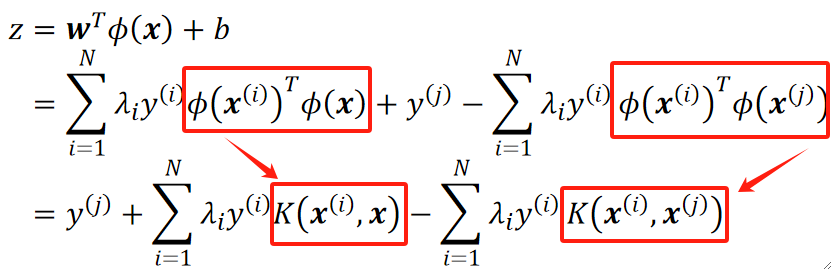
· 可以发现,式子中包含了一个\phi(x)^T\phi(x),这两个都是高维的x,我们不需要知道它们长什么样,因为这是两个向量,无论长什么样,向量点乘的结果都是一个数,我们知道这是一个数就够了,因此,我们用一个K(x^{(i)},x)来表示它们点乘的结果,这个K(x^{(i)},x)就是核函数。
· 可以看到,模型推算之后的结果不包含w、x和b,就避免了把这三个东西真的算出来。
· 那这个核函数是怎么选取的?为什么它就能代表这两个向量的结果?数学家们给出了证明,这里我们只需要大概知道结果就行。
· 根据Mercer的理论,两个高维向量的值只有在以下情况才能被核函数代替:
满足交换律:K(x^{(i)},x^{(j)})=K(x^{(j)},x^{(i)})
满足:
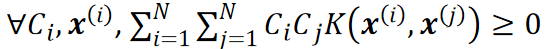
· 一些常用的核函数有:
径向基核函数(Radial Basis Function),用于映射到无穷维:
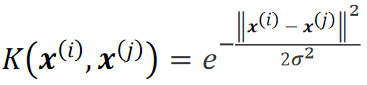
多项式核函数(Polynomial Kernel Function):
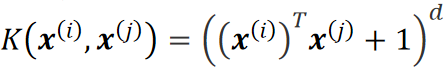
软间隔支持向量机(Soft Margin SVM)
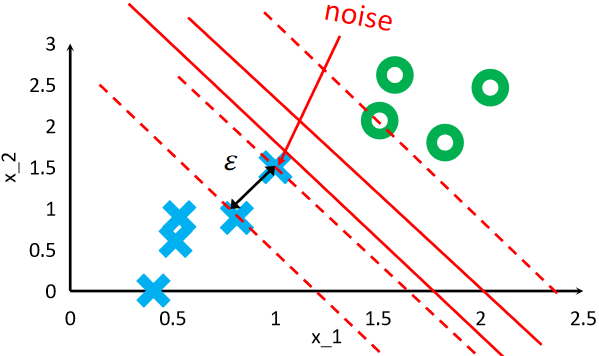
· 我们之前所讲的SVM都是硬间隔(Hard Margin SVM),它对噪声很明显,这是他的缺点。
· 因此,我们提出软间隔SVM,它可以容忍一些噪声的存在。
· 当然,容忍也不是无限制的容忍因此我们还是需要给它一点惩罚。
· 这里的惩罚我们用合页损失函数(Hinge Loss)来表示,其实就是噪声点离真正应该存在的超平面有多远:
· 合页损失函数表示为:
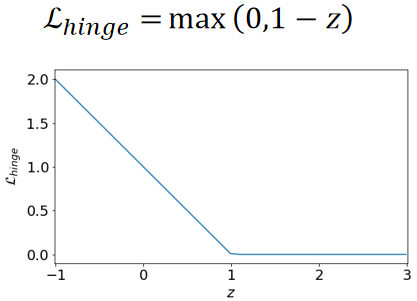
· 即![]() 。
。
· 规定好损失之后,我们要如何把它加进去呢?
· 首先要知道的是,在硬间隔中,我们是通过限制条件来定死所有的点必须满足在线的两侧的,因此,如果要让他变成软间隔,则需要在限制条件上放宽一点。
· 硬间隔(原来的):
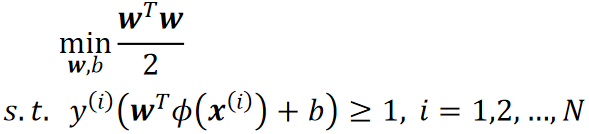
· 软间隔:
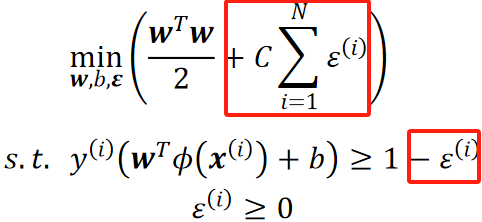
· 可以看到,在限制条件上,我们放宽了,现在点不一定要在线内,可以越出去一点了,除此之外,我们还把损失加到了需要考虑的间隔里面去。
· 同时,我们还引入了超参数C,来控制这个放宽的程度的重要性。
· 如果这个C特别大的话,接近无穷,软间隔就会退化为硬间隔;如果这个C特别小,那就是鼓励模型去犯错,这不好。
· 最后,根据对偶问题,重新求解,就可以算出软间隔的最大距离为:
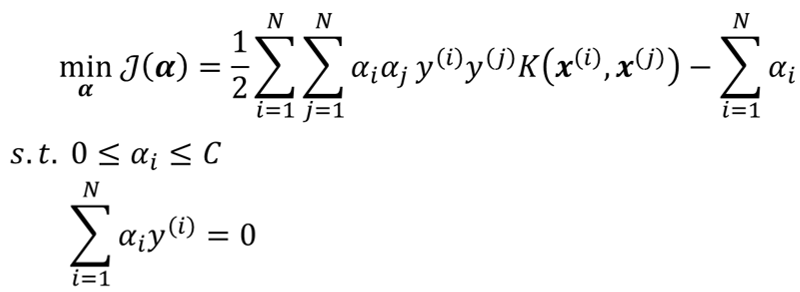
· 可以使用SMO算法去自动求解,这里不展开
