感知机
· 感知机的主要作用是用于二分类。
· 之前学习逻辑回归的时候我们的标签都是用{0,1},在感知机里,我们把标签换成{-1,+1}。
· 注意:因为标签只有2个,距离一致,故不需要转为独热向量!
举例:与问题(AND Problem)
· 我们用与问题来说明感知机这个算法。
· 既然是与问题,那给出的数据集就只有:
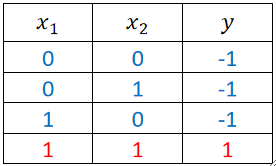
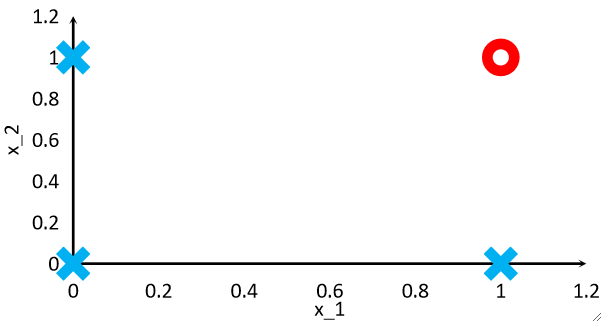
小插曲:回归任务和分类任务的最大特点是啥?
· 回归任务的标签y的取值是连续的,如y \in R。
· 分类任务的标签y的取值是离散的,如这里的y \in \{ -1, 1 \}。
模型
· 我们的模型依然是一个线性模型\textbf{z=w}^T\textbf{x}+b。即下方斜的平面。
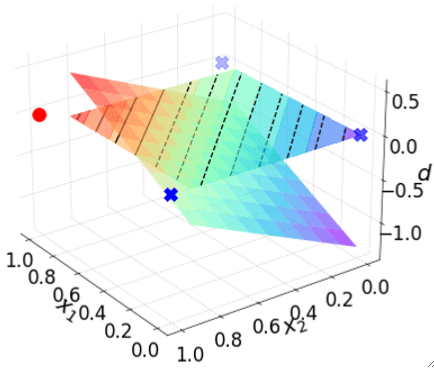
· 把模型降维到x1和x2的平面上就是:
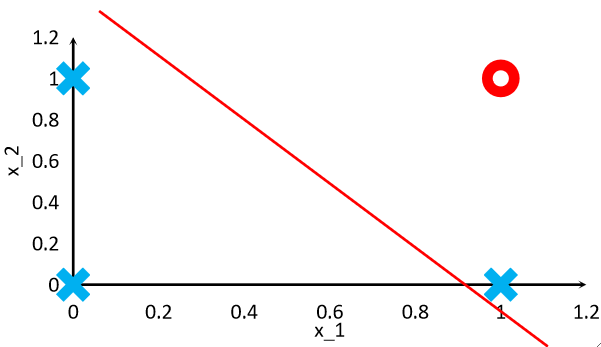
· 其实这条线的方程就是\textbf{w}^T \textbf{x}+b=0,即模型和z=0进行联立。
· 所以最终我们要训练的就是这条线,其实就是w和b,所以我们的模型是\textbf{w}^T\textbf{x}+b=0。
· 有一个小点,如果我给模型的两边乘一个\lambda,即一个系数,最终对我们的分类是没有影响的,因为其实联立之后是没变的,因为右边是0,只是切的陡一点还是平一点而已,但还是那条线。
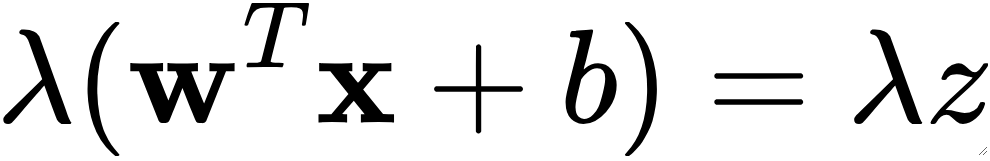
· 然后,我们计算一个样本点到决策面(超平面)的距离,公式如下:
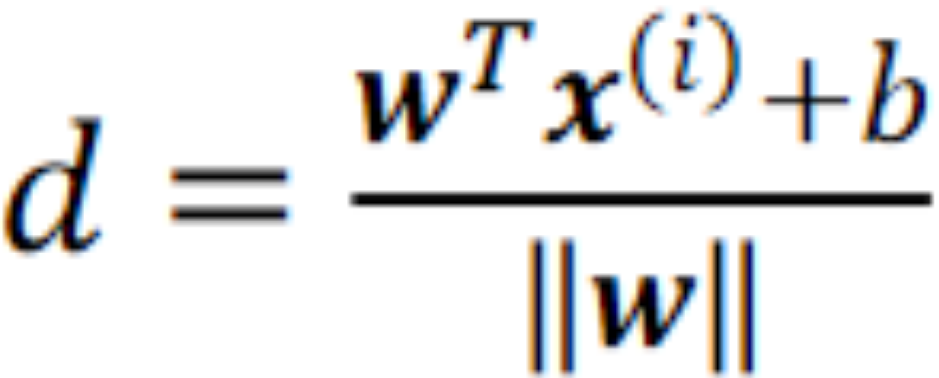
· 有意思的是,我们发现,距离公式里面没有绝对值,即d有正负。
· 因为我们需要通过大于0还是小于0来区分两类,只需要简单的过一个符号函数即可:
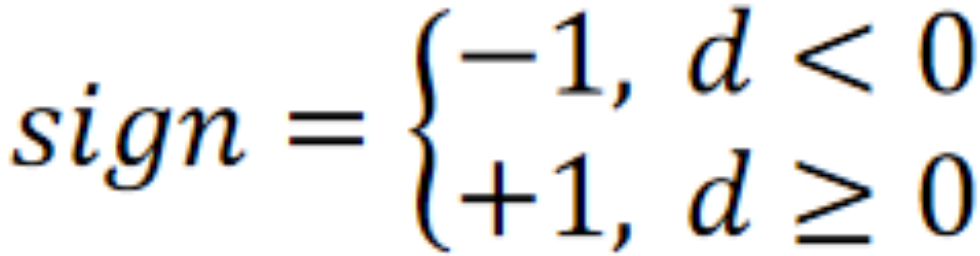
· 这里有一个点,我们算出来d,只是想要它的正负罢了,对于值我们不在乎,因此理论上来说可以乘一个任意正数。
· 因此我们给d乘一个||w||,这样做的好处就是简化计算:
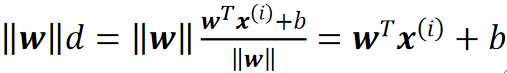
· 这样我们就只用算w^Tx+b就好了。
· 或者从另一个角度理解这个点,我们刚刚说了,给模型乘一个\lambda不会影响我们后面的决策,其实,d的公式不就是给模型乘了一个\frac{1}{||\omega||}而已嘛,现在我们又乘了一个||w||,只是变回去了而已,无论如何都不影响最后的决策。
· 乘完了||w||之后,d又变回了模型z了,所以最后殊途同归。
· 最终的模型如下:
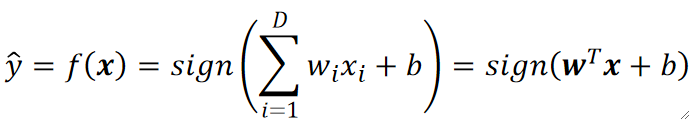
损失函数
· 因为模型是从距离上定义的,所以我们的损失函数也是从距离上定义的。
· 我们把损失定义为,所有做错了的点的到决策面的距离的和:
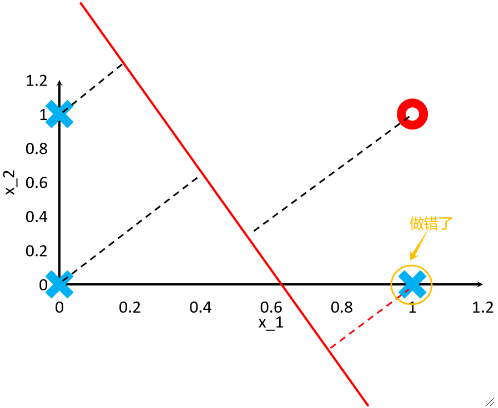
· 所以我们的公式为:
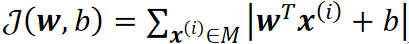
· 其中M是所有做错了点,值得注意的是,这里的“距离”是乘了||w||之后的,并且需要加绝对值,因为损失不关心哪边错,只关心错多少。
· 虽然看上去没什么问题,但是实际上却很麻烦,首先,我们要如何界定一个点是否做错?其次,后面梯度下降的时候绝对值求导很痛苦,这都不是我们所希望的。
· 这个时候,我们把标签改为{-1,1}的好处就来了。我们让标签y hat去乘上距离,如果结果小于0,就肯定是分错了的!
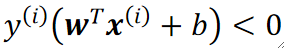
· 同理,我们的损失函数就能重新定义为:
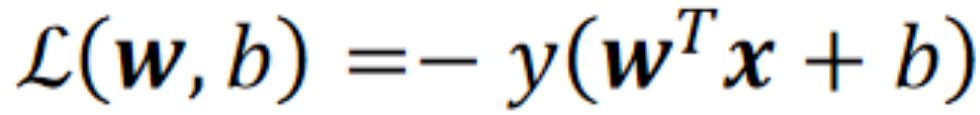
· 注意要加一个负号才是正的哦!
· 这样我们的代价函数就是:
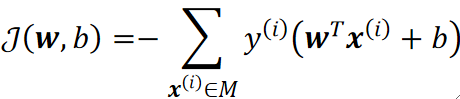
优化
· 最后就是通过梯度下降来优化。
· 有意思的是,感知机并不使用Full Batch去梯度下降,而是随机选一个,使用随机梯度下降。
· 对损失L去求偏导,dL/dw,对于某一个wi,最终求得的偏导很简单,就是-y^{(i)}x^{(i)},同理对b求偏导就只有-y,所以参数更新就是:
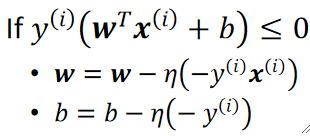
· 注意,每次只选一个点去判断,所以是随机梯度下降。
· 一直更新,直到没有错误或达到迭代次数就停止。
总结
· 虽然感知机可以分出两类来,但是不一定能找到最优解,如果希望在这么多种可能的结果里面找到最优解,就需要使用支持向量机SVM。
· 或者我们也可以加入非线性元素,即使用神经网络去进行激活。
