信息隐藏的基本特征
不易察觉型
· 也叫透明性和隐蔽性,是指秘密信息的嵌入不改变原数字载体的主观质量和统计规律,不易被观察者和监视系统察觉。
鲁棒性
· 指嵌入水印后的数据经过各种处理操作和攻击操作后,不导致其中的水印信息丢失或破坏的能力。
· 如图像文件经过缩放、裁剪、旋转、有损压缩等操作,隐藏信息不丢失。
隐藏容量
· 它是指在隐藏秘密数据后仍满足不易觉察性的前提下,数字载体中可以隐藏秘密信息的最大比特数。
图像信息伪装技术
伪装的基本原理
· 任何多媒体信息,在数字化时,都会产生冗余(数据冗余与感官冗余),冗余也可视为一种物理随机噪声,而人的感观系统对这些随机噪声是不敏感的。
· 伪装就是利用这个原理,试图用秘密信息比特替换掉冗余数据(随机噪声),以达到隐藏秘密信息的目的。
图像的冗余空间
· 图像的低4bit,我们通常认为可以做隐藏信息的空间,也就是载体的冗余空间。

· 由上面的对比可以看到,虽然图像矩阵的每个像素值都去掉了低4bit,但改变后的图像和原图像在给人的视觉上并没有太大的变化,因此可以认为低4bit是冗余空间,可以改变,这是可以进行图像嵌入伪装的理论基础。
直接4Bit替换法
· 直接用秘密图像像素点高4位去替换载体图像像素值的低4位。
· 首先,提取图像信息并分层:
cover = imread('lenna.bmp');
data = cover;
msg = imread('woman.bmp');
[row, col] = size(cover);
# 把图像的R层作为载体图像
cover1 = cover(:, :, 1);
· 然后,我们处理载体图像和秘密图像的低四位:
# 置载体图像R层的低四位为0
cover1 = bitand(cover1, 240);
# 置秘密图像的低四位为0
takemsg4 = bitand(msg, 240);
# 将秘密图像的高四位右移4位
shiftmsg4 = bitshift(takemsg4, -4);
· 让我们进行图像隐藏并保存:
# 图像隐藏
cover1 = bitor(cover1, shiftmsg4);
# 写回并保存
data(:, :, 1) = cover1;
imwrite(data, 'mix.bmp');
· 然后我们来尝试提取一下秘密图像:
# 提取秘密图像信息
data = imread('mix.bmp');
[row, col] = size(data);
A = data(:, :, 1);
# 提取隐蔽图像的低四位
A = bitand(A, 15);
# 将提取的秘密图像的低四位左移四位
A = bitshift(A, 4);
· 对于隐藏在R、G、B各层的隐蔽载体,会产生泛红、泛绿、泛蓝现象。
· 为了改进,可以将秘密图像像素值的高四位分别藏于载体图像R、G、B层像素值的最低位或次低位。
· 还有一个问题,直接4Bit替换法鲁棒性弱、安全性差(无密钥机制):

图像置乱
· 所谓“置乱”,就是将图像的信息次序打乱,将a像素移动到b像素的位置上,b像素移动到c像素的位置上……使其变换成杂乱无章难以辨认的图像。
· 置乱实际上就是图像的加密,与加密保证安全性不同的是,将置乱的图像作为秘密信息再进行隐藏,在提高系统安全性的同时可以很大限度的提高隐蔽载体的鲁棒性。
· 图像置乱的模板变换如下:
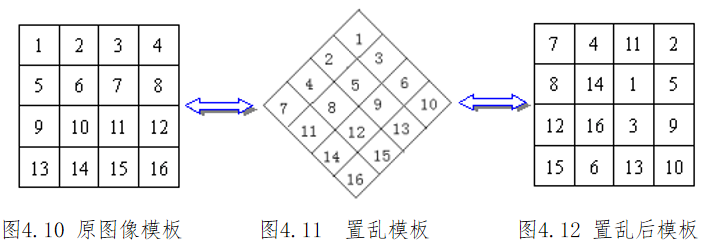
· 置乱的优点——增加图像伪装的鲁棒性。
· 例子:

空域下隐藏:替换隐写技术
· 我们知道,任何多媒体信息,在数字化时,都会产生物理随机噪声,而人的感观系统对这些随机噪声是不敏感的。
· 替换技术就是利用这个原理,试图用秘密信息比特替换掉随机噪声,以达到隐藏秘密信息的目的。
LSB替换隐写
· LSB是Least Significant Bits的英文缩写,对应的中文意思是:最不重要位。有时也称之为最低有效位或简称最低位。
· 隐写过程如下:
在c中根据密钥k选择l(m)个像素。
对于选取的每个像素灰度值,若其LSB与要嵌入的信息比特相同,不进行更改;否则,执行下一步;
用秘密信息比特取代原灰度值的LSB,而高7位保持不变,修改后的图像即为s。
· 看一个例子:
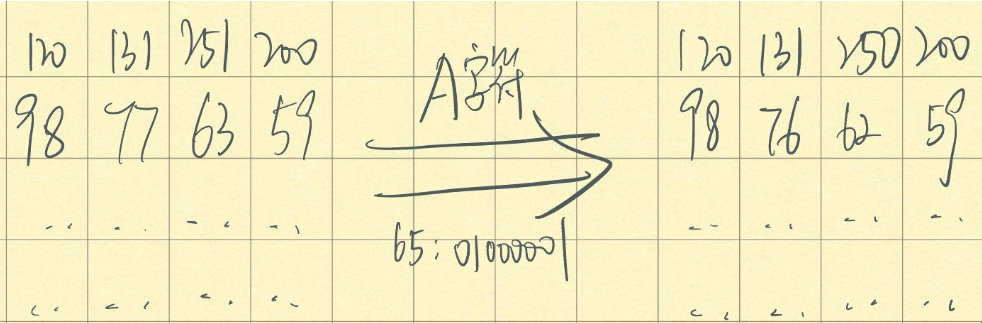
· 要在原图像嵌入一个字符A,首先知道A的ASCII码为65,转换为对应二进制为01000001,然后一个个对着嵌入即可。
· 120要嵌入0,不用动;131潜入1,不用动;251要潜入0,要减一,变成250;以此类推。
· 如果遇到奇数要嵌入0,则要变成1,即+1;遇到偶数要嵌入1,则要变成0,即-1。
二值图像的隐写(重点)
· 解决方案1:利用图像特定区域中黑像素的个数来编码秘密信息。
· 定义符号P_1(B)代表一个区域Block内1值的占比。如P_1(B)=0.5,代表图像中一半白一半黑。
· 如果P_1(B)>0.5,则代表嵌入1,否则嵌入0。但这样就会出现问题:
如果一个块内要嵌入0,但是白色比黑色多,即P_1(B)<0.5,就要找边缘去填充一些黑点让P_1(B)>0.5。但如果本身这么块里面黑白比例很悬殊,比如全是黑或者全白,那说明这一块不适合嵌入,应该跳过。
如果一个块内黑白像素点比例很接近,如白点的占比是0.51,应该嵌入1,但我想嵌入0,最方便的方法就是删掉一两个白点,但这样鲁棒性就很低,别人可以通过轻易加上一两个白点来破坏。因此我们需要优化我们的编码方案,原来我们的阈值是0.5,现在应该改为双阈值,即P_1(B)<0.45的时候嵌入0,P_1(B)>0.55的时候嵌入1,中间0.45到0.55我们称为隔离区,这样我们就可以增加鲁棒性,别人破坏的点可以更多一点。
对于第一点提到的问题,黑白比例悬殊就应该跳过这一块,因此我们需要设置最左边和最右边为无效块,但这样又会诞生一个问题,和第二点一样,一点点的变化很难区分是不是无效块,因此还是需要给出一小段距离用于容错。
· 为了解决上述提出的问题,最终我们把P_1(B)可能的取值分为下面几块:

· 上图是嵌入时候的规则,对于提取,可以放宽,就用是不是50%来判断即可。
· 边界点定义:对于某一个点,其相邻的8个方向的像素,只要有一个值和自身相反,就认为这个点是边界点。
· 如何修改边界点:直接取反即可。
· 边界扩散现象:
如下图中,B很明显是个边界点,要取反:
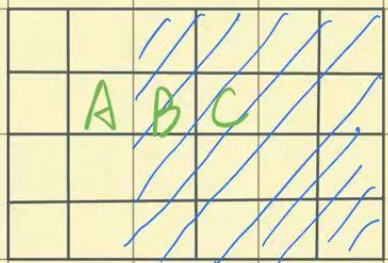
取反之后变为下图,此时C就变为边界点了,那C也应该取反,但这不是我们所希望的,如果一直取反下去,就会造成突出或凹入的毛刺。

为了防止这种边界扩散现象,只需要对取反后的点+0.01,这样C和B就不是相反了,就不会一直取反下去了。
· 我们来把这些区域切割开来分类讨论:
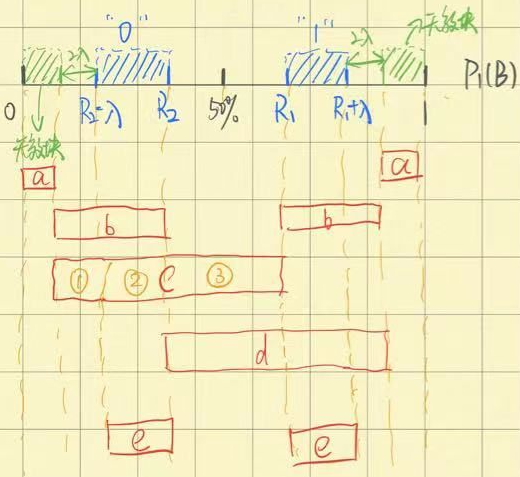
对于落入b区间的比例,假设是左边的b区间,如果要嵌入0就很好,直接嵌入就行;如果要嵌入1,则多加白点,让他进入左边的a区间,即无效块,让这一块无效;因为如果要多加白点很难实现。
对于落入c区间的比例,假设是左边的c区间,如果是要插入0,则落入①、②的话交给b区间处理即可,若落入③则多加一点白点,让它往②靠;如果是要插入1,则落入①、②的话直接加白点使其无效,若落入③则交给d处理即可。
对于落入e区间的比例,其实就是b、c都处理了,这里不再赘述。
· 接下来我们讨论一下这个算法的性能,其实就是在讨论R0、R1的距离和λ。
· 如果R1和R2的距离增大:
鲁棒性增加,因为中间无效区域增大,容错性大。
无效区a变窄,有效区c、d变宽,容量增大。
要修改的像素点数量变多,这样就会使边界不足现象增加。
· 如果λ变大:
鲁棒性增加,因为中间无效区域增大,容错性大。
无效区a变窄,有效区c、d变宽,容量增大。
要修改的像素点数量变多,这样就会使边界不足现象增加。
· 可以发现,无论是R0、R1的距离增大还是λ变大,导致的结果都一样。
· 对于提高透明性的讨论:
只修改边界点。
引入无效块以保证修改的边界点数量尽可能少。
防护边界扩散现象。
可以先置乱块,再嵌入。
对于查找边界点进行取反的过程,可以按置乱的顺序去查找而不是从上到下从左到右。
· 对于容量的讨论:
一张512*512的图像,可以分成2601块10*10的块。按照上面的算法筛选完后,只有105块可用,即105个bit可以嵌入,即10几个byte,即10几个字符,太少了。
根据上面的结论,增加R0、R1的距离,增大λ,可以增加容量。
选用尽可能大尺寸的图像也可以增加容量。
采用合适的二值化图像算法来生成二值化图像。我们一直使用的是阈值二值化,可以尝试误差扩散抖动技术来二值化,这样产生的二值化图像可以大幅提升容量。
· ----------------------------------------------------------------------
· 解决方案2:利用游程长度编码(Run Length Encoding,RLE)。
· 水平方向扫描二值图像,在一条扫描线上做编码。如果左右的值一样,则标记为一个游程,记录第一个的位置以及长度。
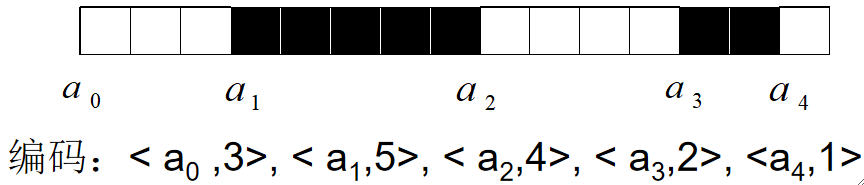
· 然后,通过游程长度的奇偶性来决定嵌入0还是1,假设我规定嵌入1时游程长度为偶数,嵌入0时长度为奇数,这样只需要把边界的那一个像素进行翻转即可实现。
· 这样保证了透明性,因为只修改了边界。
· 容量也不错,这取决于边界点的数量,即游程的数量。
· 但是鲁棒性很差,因为只要我对图像的长度做任意修改,就完全破坏了原来的游程。
· 还有一点,一开始就要规定好是修改头的点还是尾的点,一旦规定后续不能修改!
· 例题:给出游程编码<a0, 3>,<a1, 4>,<a2, 4>,<a3, 5>,嵌入规则为【0-长度为偶数,1-长度为奇数】,约定游程长度在2i到2i+1变换,现要求嵌入1100时,写出新的游程编码。
首先我们把题目给出的已有的游程编码写出来:

然后开始重新编码,第一个是1,a0长度为奇数,不用变。
第二个是1,a1长度为偶数,长度要变,因为给出范围是2i-2i+1,因此4要变成5,吃掉一个a2的位置:

然后第三个是0,此时a2的长度已经从4变为3了,因此a2也要变,根据范围,a2长度3要变成2,多出来的位置给a3:

最后一个是1,此时a3已经是奇数了,所以不用管。
最后得到的新的游程编码为<a0, 3>,<a1, 5>,<a2, 2>,<a3, 6>。
· 值得注意的是,游程要求长度至少为2,如果是1则是无效游程,因为如果它被翻转,就和其它游程融合了,这样会改变游程的数量。
· 最简单的处理方法就是先对图像做预处理,先对只有一个像素的游程点做翻转。大部分情况下,单像素的游程基本都是噪声。
频域下隐藏:离散余弦变换(DCT)
· DCT是一种实数域变换。在中频中做信息隐藏,同时保证了鲁棒性和透明性。
两点法
· 先把图像分成一个个8*8的小块,分别选其中的两个点,如(μ1, v1),(μ2, v2)。
· 若Bi(μ1, v1)>Bi(μ2, v2),代表隐藏1;如果相反则交换两系数。
· 若Bi(μ1, v1)<Bi(μ2, v2),代表隐藏0;如果相反则交换两系数。
· 这里的交换两系数指的是:我规定了第一个值比第二个值大才嵌入1,现在这个块要嵌入1,但第一个值比第二个小,这个时候我在图像上直接把这两个值对调。
· 两点法的特点是:
不需要原始图像。
对JPEG图像压缩是鲁棒的。
三点法
· 同样的,先把图像分为一个个8*8的小块,然后接下来用伪代码展示:
# 取三个点
Bi(u1, v1);
Bi(u2, v2);
Bi(u3, v4);
# 获取三者中谁最大谁最小
max = max(...);
min = min(...);
# 定义一个系数D
D = ...;
# 定义一个值MD,用于后续衡量
MD = ...;
# 若规定嵌入1的时候,Bi(u3, v3)要是三者中最大的
if Bi(u3, v3) == max:
# 让Bi(u3, v3)大的更明显,D人为设定
Bi(u3, v3) = Bi(u3, v3) + D;
else if max-Bi(u3, v3) < MD:
# Bi(u3, v3)与最大值离得不远
Bi = max + D;
else:
(设定该块为无效块)
Bi(u3, v3) = (Bi(u1, v1) + Bi(u2, v2)) / 2;
# 若规定嵌入0的时候,Bi(u3, v3)要是三者中最小的
if Bi(u3, v3) == min:
# 让Bi(u3, v3)小的更明显
Bi(u3, v3) = Bi(u3, v3) - D;
else if Bi(u3, v3) - min < MD:
# Bi(u3, v3)与最小值离得不远
Bi(u3, v3) = min - D;
else:
(设定该块为无效块)
Bi(u3, v3) = (Bi(u1, v1) + Bi(u2, v2)) / 2;· 设置为无效块的方法很简单,就是把Bi(u3, v3)的值设置为Bi(u1, v1)和Bi(u2, v2)的中间即可:
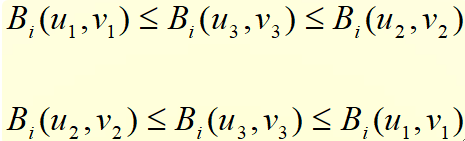
· 例题:使用三点法隐藏,给定规则为,隐藏1的时候,令Bi(u1, v1)>Bi(u3, v3)+D且Bi(u2, v2)>Bi(u3, v3)+D,问:
补全余下的规则,即隐藏0的规则是什么?
1的时候Bi(u3, v3)要小的很明显,那么0的时候就让Bi(u3, v3)大的很明显即可。
已知三个点的DCT系数值为(1.6, 2.1, 1.0),(0.7, 1.2, 1.8),(0.9, 1.9, 1.4),问根据给定规则能提取出什么?
第一个,Bi(u3, v3)是最小的,那就是提取出1;第二个,Bi(u3, v3)是最大的,那就是提取出0;第三个Bi(u3, v3)处于二者中间,无效。
