概述
· 数学形态学是以形态为基础对图像进行分析的数学工具。
· 基本思想是用一定形态的结构元素去探测图像中的对应形状以达到对图像分析和识别的目的。
· 数学基础和所使用的语言是集合论。
· 数学形态学可用于简化图像数据,保持它们基本都形状特性,并去除不相干的结构。
· 本章将介绍二值数学形态学的基本运算和运用。
结构元素
· 用形态学去处理图像的基本思想是利用一个结构元素去探测一个图像,看是否能够将这个结构元素填放在图像的内部,同时验证填放结构元素是否有效。
· 如下给出一个绿色的图像和一个结构元素,可以看到,在左边,结构元素可以很好地填放在图像内部,而右边的那个不行。
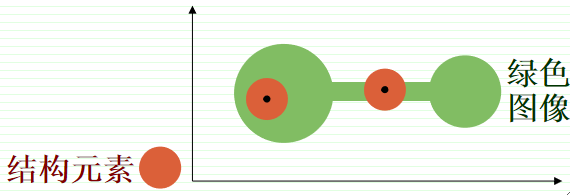
· 通过上图看到,通过对图像内合适放入结构元素的位置作标记,便可得到关于图像结构的信息。
· 这些信息与结构元素的尺寸和形状有关。因而这些信息的性质取决于结构元素的选择。也就是说,结构元素的选择与从图像中抽取何种信息有密切的关系。
· 因此,我们可以构造不同的结构元素,便可完成不同图像分析,达到不同的分析结果。
平移
· 形态学的处理都基于填放结构元素的概念。而利用结构元素填充的过程,取决于一个基本欧式空间运算——平移。
· 将一个集合A平移距离x可以表示为A+x,可以定义为:
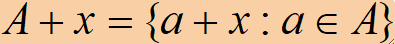
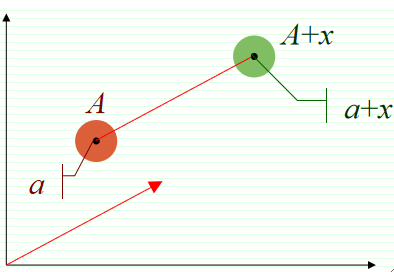
· 从几何上看,A+x表示A沿矢量x平移了一段距离:
腐蚀运算(Erosion)
· 集合A被集合B腐蚀,表示为A \ominus B:
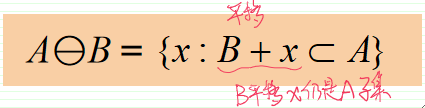
· A为输入图像,B为结构元素。
· 如果将B看作模板,那么,A \ominus B则是由在模板平移的过程中,所有可以填入A内部的模板的原点组成。
· 腐蚀具有收缩图像的作用。
腐蚀运算的几何解释
· 如下图,结构元素B是一个圆盘,从几何角度看,圆盘在A内部移动,将圆盘道原点位置(圆心)标记出来,便可得到腐蚀后的图像。
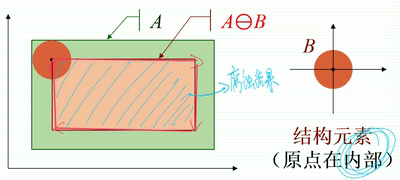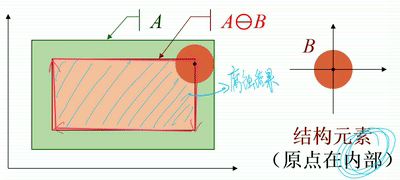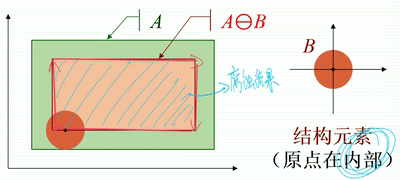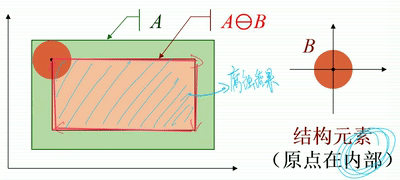
· 注意,上述例子中,原点是在结构元素内部的,那么腐蚀后的图像是输入图像的一个子集。
· 如果原点在结构元素的外部,那么腐蚀后的图像则不一定在输入图像的内部。
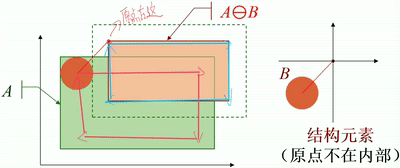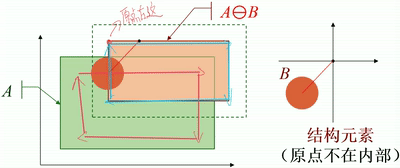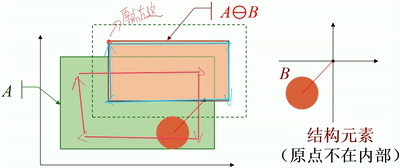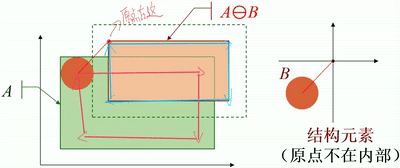
· 可以看到,上图结构元素B的原点在自身的右上角,那么腐蚀出来的图像则不在输入图像的内部。
· 一些腐蚀运算的例子:
原点包含在结构元素内:
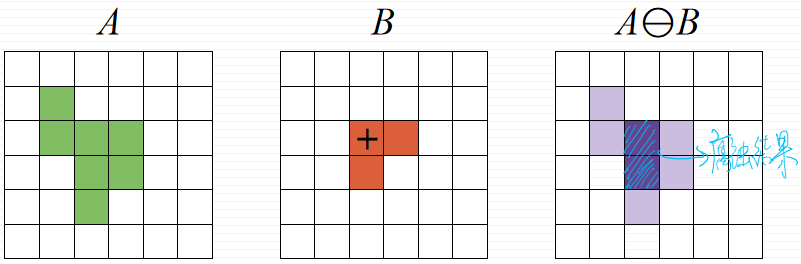
原点不在结构元素内:
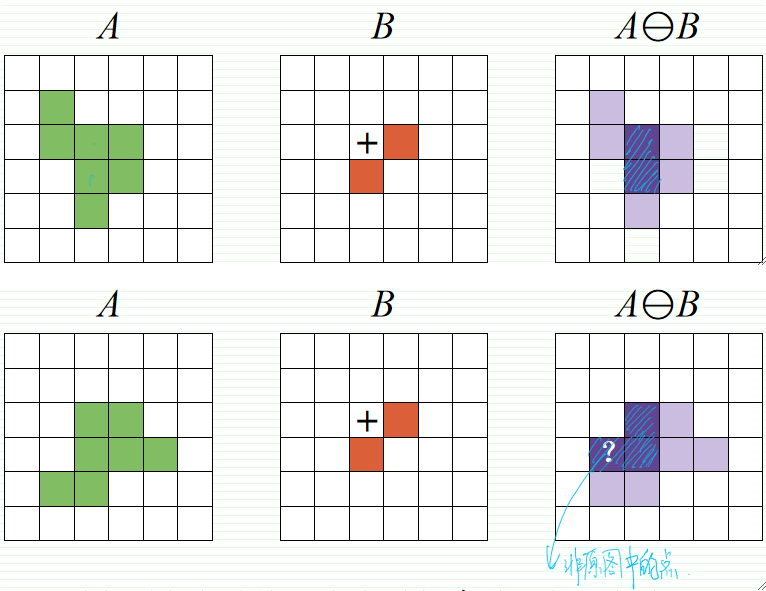
膨胀运算(Dilation)
· 集合A被集合B膨胀,表示为A \oplus B,定义为:
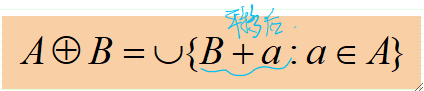
· 其中A为输入图像,B为结构元素。
· 膨胀可以通过相对输入图像的所有点平移结构元素,然后计算其并集得到。
· 膨胀具有扩大图像的作用。
· 膨胀满足交换律,因此上式还可写成:
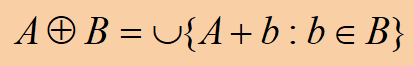
膨胀运算的几何解释
· 如下图,图中结构元素为一个圆盘。
· 从几何角度看,圆盘的原点在A的内部移动,对各个平移后的圆盘(不是原点!)求并集,就是膨胀后的图像。
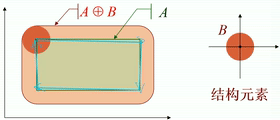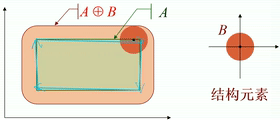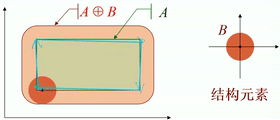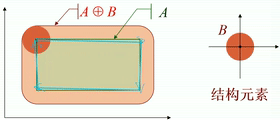
· 如果原点在结构元素的内部,则输入图像一定为膨胀后图像的一个子集。
· 如果原点在结构元素的外部,则输入图像一定不在膨胀后图像的内部。
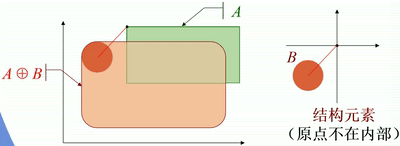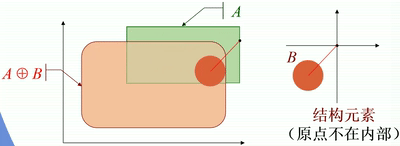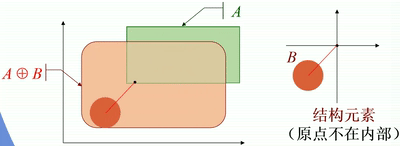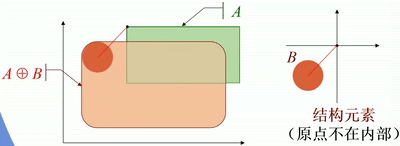
· 一些膨胀运算的例子:
原点在结构元素的内部:
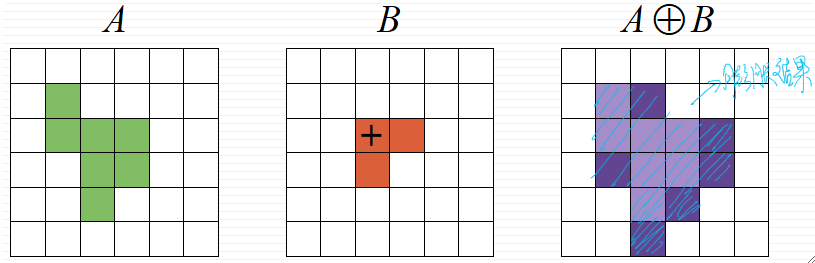
原点不在结构元素内部:
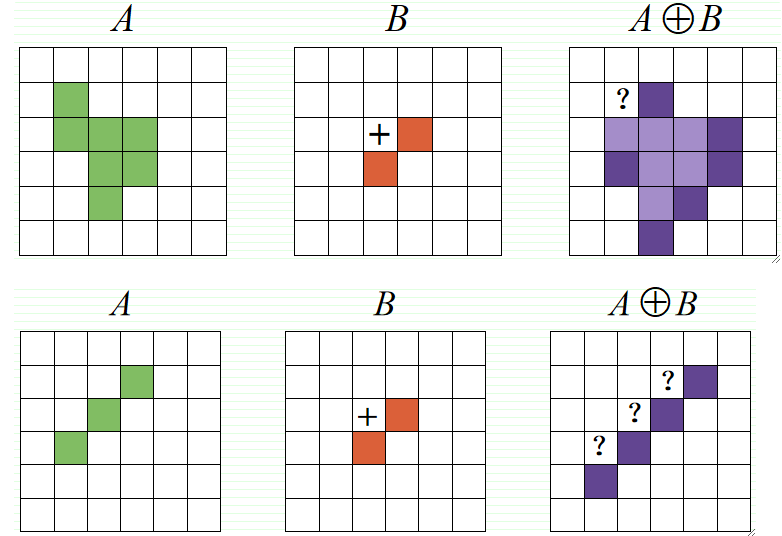
开运算(Opening)
· 使用结构元素B对集合A进行开运算,定义为:
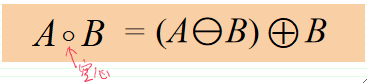
· 即先用B对A进行腐蚀,再用B对腐蚀结果进行膨胀。
· 开运算可以使图像的轮廓变得光滑(去噪),断开狭窄的间断和消除细的突出物。
· 开运算可以通过计算所有可以填入图像内部的结构元素平移的并求得。
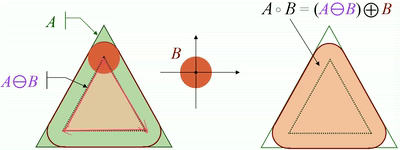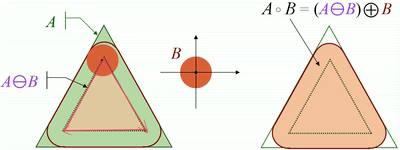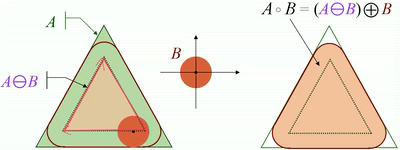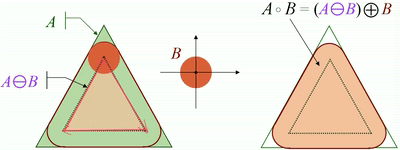
闭运算(Closing)
· 使用结构元素B对集合A进行闭运算,定义为:
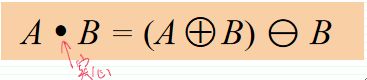
· 即先用B对A进行膨胀运算,然后再用B对膨胀结果进行腐蚀。
· 闭运算同样可以使图像的轮廓变得光滑,但与开运算相反,它能消除狭窄的间断和长细的鸿沟,消除小的孔洞,并填补轮廓线中的裂缝,也可以去噪。
· 开闭运算区别:
开运算是锉刀,打磨图像,所以最终会少东西。
闭运算是填缝剂,会多东西。
· 将结构元素沿着图像的外边缘进行滚动,滚动边界形成的闭合区域就是闭运算的结果:
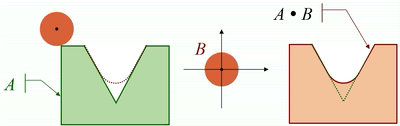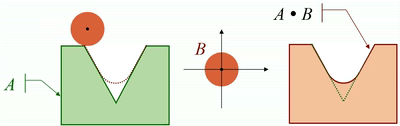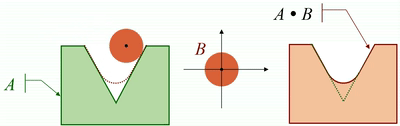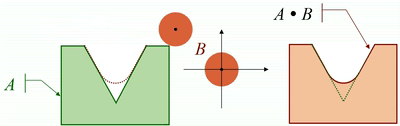
开闭运算的性质
· 开运算使原图缩小;闭运算使原图扩大。
· 若C是D的子集,则C \circ B是D \circ B的子集。
· 若C是D的自己,则C \bullet B是D \bullet B的子集。
· (A \circ B) \circ B = A \circ B
· (A\bullet B) \bullet B = A \bullet B
