图像变换基础
· 定义:图像变换指的是把原定义在图像空间的图像以某种形式转换到另外一些空间。
· 作用:在不同的空间下,图像会有不同的特性,掌握图像变换技术,可以在不同的空间下思考问题,并利用不同空间的优越性解决问题。
· 之前我们一直使用的,熟知的图像空间为“空域空间”,但经过傅里叶变换后,可以获得图像的“频域空间”。
信号的分解
· 信号:带有信息都物理量。比如,灰度图像,像素的灰度值就是它携带的信号。
· 信号分解是利用化繁为简、化整为零的思路,将一个复杂的信号分解为一系列“简单”信号的特定组合(叠加)。
· 那什么样的信号才是我们需要的简单信号?
· 简单信号:一组信号彼此完全不相似,它们互相不包含对方的分量。这种性质在数学上也被称为正交性。
· 两个函数正交的充要条件是它们的内积为0。函数f1(t),f2(t)在(t1, t2)上的内积定义如下:
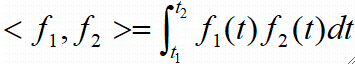
· 那有哪些函数集是自然正交的呢:
在实函数中,有一组自然、和谐的函数非常适合作为正交函数集——正弦余弦函数。
对于任何的sin(nx)cos(mx),sin(nx)sin(mx), cos(nx)cos(mx)(n≠m)在一个周期内,即(-π, π)的面积相加起来总是零。
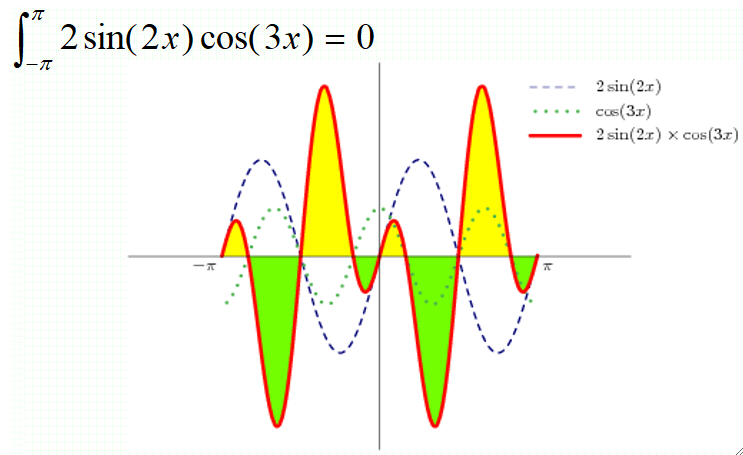
在复变函数中,可以证明,复指数函数集\{e^{jnwt}, n \in Z\}也是一个完备的正交函数集。
从某种意义上讲,复指数函数与三角函数本质上是一致的,因为欧拉公式连接了他们:e^{j\theta} = \cos\theta + j\sin\theta
,代入\theta为\pi有e^{j\pi} + 1 = 0 。
· 现在我们知道了需要的简单信号是类似正余弦三角函数、复指数函数的正交信号。那它们遵循什么样的组合规律呢?
· 信号分解为三角函数:一个周期为T的信号f(t),可以展开成三角函数(信号)的叠加:
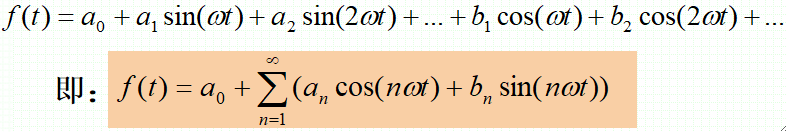
这种展开式称为三角形式的傅里叶级数,其中w=2\pi/T是信号的角频率,a_n、b_n为傅里叶系数。
· 已知f(t),确定傅里叶系数a0、an和bn:
直流分量系数(零频系数):{a}_{0}=\frac {1} {T}\int ^{}_{T} {f(t)dt}
余弦分量系数:{a}_{n}=\frac {2} {T}\int ^{}_{T} {f(t)cos(n\omega t)dt}
正弦分量系数:{b}_{n}=\frac {2} {T}\int ^{}_{T} {f(t)sin(n\omega t)dt}
· 信号分解为复指数函数:一个周期为T的信号f(t),展开成复指数函数的叠加:
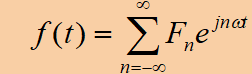
· 则傅里叶系数Fn可以按照以下公式求得:
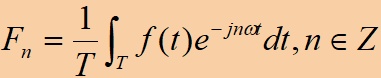
· 至此,信号的分解就讲完了,简单总结一下,一个复杂信号可以用许多简单信号“加起来”表示,利用函数的正交性找到这些简单信号,并通过计算得出叠加的系数。
· 现在,就可以解答什么是频域空间了。
· 看一个例子,有一个信号f(t),它可以用正弦波表示:
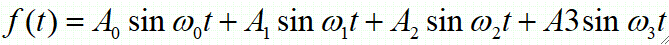
· 这样,我们可以写出它的幅度A与频率w四队:
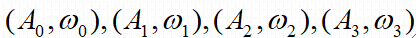
· 这样,我们就可以认为这四组数对唯一确定了信号f(t),换句话说,这四组数对是信号f(t)的另一种表达方式。
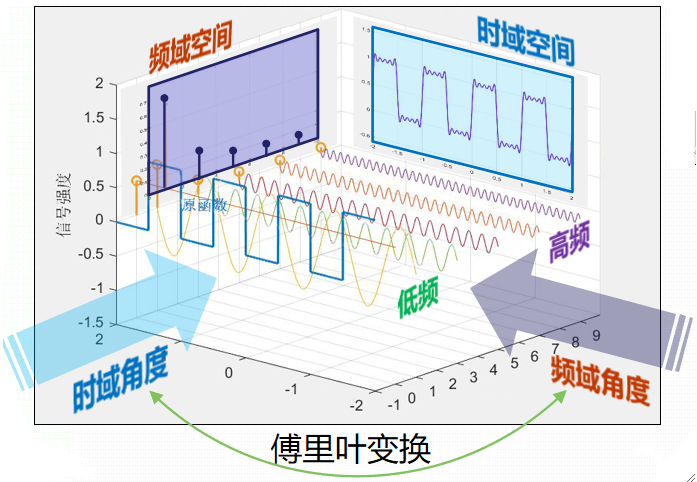
· 这四组数对构成的空间就是所谓的频域空间,它与时(空)域空间完全等价。
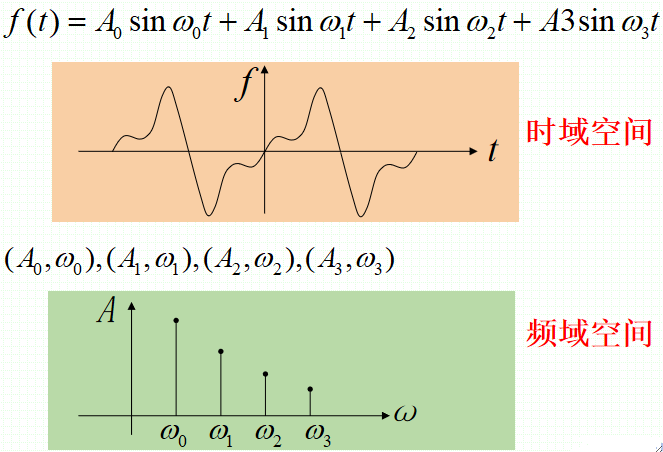
· 我们可以从一张图更清晰的看到两个空间:
傅里叶变换定义
一维连续傅里叶变换及反变换
· 单变量连续函数f(t)的傅里叶变换F(μ)定义如下,其中x是时域变量,μ是频域变量,j^2=-1。
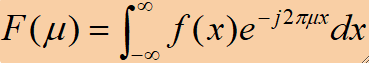
· 给定F(μ),通过傅里叶反变换可以得到f(x):
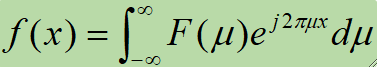
· 傅里叶变换中的变量μ通常称为频率变量,这个名称源于欧拉公式中的指数项,我们把\theta代入2πμx就有:
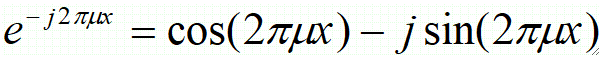
· 如果把傅里叶变换的积分解释为离散项的和,则易推出F(μ)是一组sin和cos函数项的无限和,μ就决定了相应sin、cos的频率。
· 从公式我们可以知道,傅里叶变换的结果F(μ)是一个复数表达式,设F(μ)的实部为R(μ),虚部为I(μ),则有:
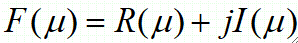
· 这样我们就可以得到幅度谱、相位谱、能量谱:
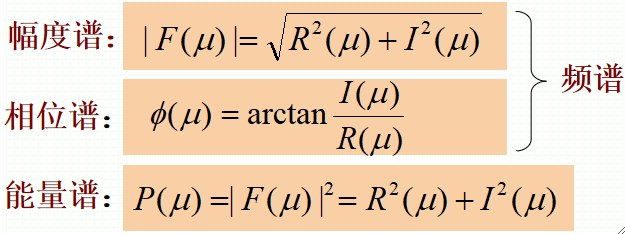
二维连续傅里叶变换及反变换
· 仿照一维连续傅里叶变换,我们可以得到二维连续函数f(x, y)的傅里叶变换F(μ, v)定义为:
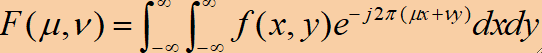
· 其中x,y是时域变量,μ,v是频域变量,j^2=-1。
· 给定F(μ, v),通过傅里叶反变换可以得到f(x, y):
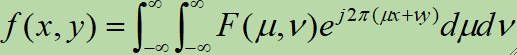
· 同理,记傅里叶变换的实部为R(μ, v),虚部为I(μ, v),则有:

一维离散傅里叶变换(DFT)及反变换
· 单变量离散函数f(x)(x=0, 1, ..., M-1)的傅里叶变换F(μ)定义为:
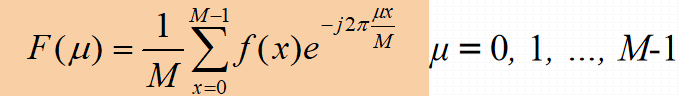
· 给定F(μ),通过傅里叶反变换可以得到f(x):
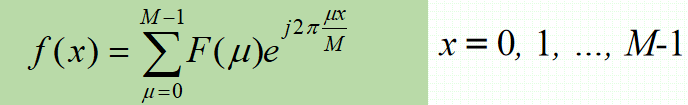
二维离散傅里叶变换及反变换(数字图像)
· 一个图像,尺寸为M*N,则其函数f(x, y)对应的DFT为:
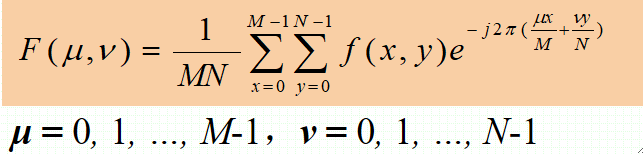
· 给定F(μ),通过DFT反变换可以得到f(x, y)有:
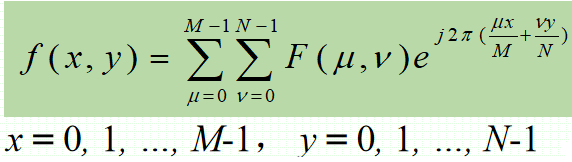
重点:离散一维傅里叶变换的计算
· 例:给出一维函数的四个采样值为f(0)=2,f(1)=3,f(2)=f(3)=4,求四个值的傅里叶变换。
· 计算过程如下:
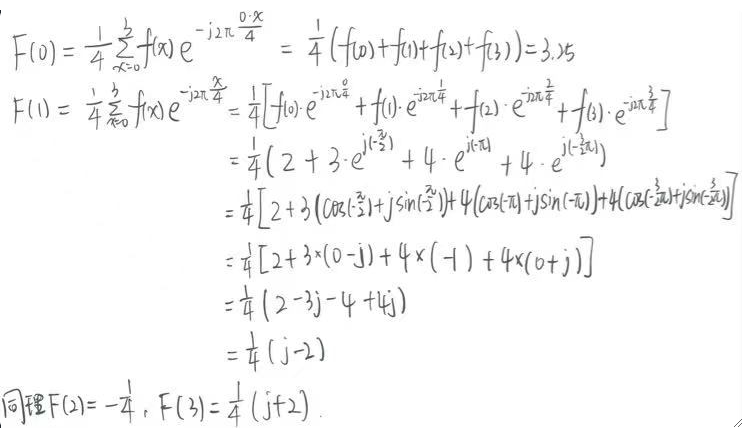
· 值得注意的是,函数f(x, y)的傅里叶变换是f(x, y)积分(连续)或累加和(离散),因此,计算每个点的傅里叶变换值,原函数f(x, y)的每一个点都需要参与。
· 因为f(x, y)的全部值都会对DFT产生影响,那么,F(μ, v)的系数改变也会对反变换结果造成影响。
二维离散傅里叶变换的显示
· 将二维频率空间的每个点的幅值,即实部和虚部平方和的平方根,规格化为显示灰度级(0-255),产生的图像即为傅里叶频谱幅度图像。

· 通常,在显示傅里叶频谱幅度图像时,需要把原点平移到图像的中心,让图像能量集中在图像中心的位置,以便能清除地分析变换谱的情况。

· 越靠近中心的点,对应的频率越低。亮度越大,表示该点对应频率的幅值越大。
· 注意,频谱图上的各点与图像上的各点不存在对应关系!
图像频域空间的物理意义
· 通过信号分解,将图像的灰度分布函数变换为频率分布函数。
· 图像的频率用于表征图像中灰度变化的剧烈程度,也成为梯度。如大面积的沙漠在图像中是一片灰度变化缓慢的区域,对应的频率值就很低;而对于地表这种变化剧烈的边缘区域,在图像中就是一篇灰度变化剧烈的区域,对应的频率值就比较高
· 频率的幅值表示该频率成分对原来图像信息(能量)的贡献。
· 我们从绘画的例子中来理解频域空间,一般我们用宽大的画刷,画出来的细节就少,这就是低频,它主要用于铺大关系;我们用细小的画刷,就能更好地刻画细节,这就是高频,它主要用于刻画细节。在空域角度上,我们就可以看到,高频的信息很少,因为细节很少,而低频的信息就比较多,细节较多。
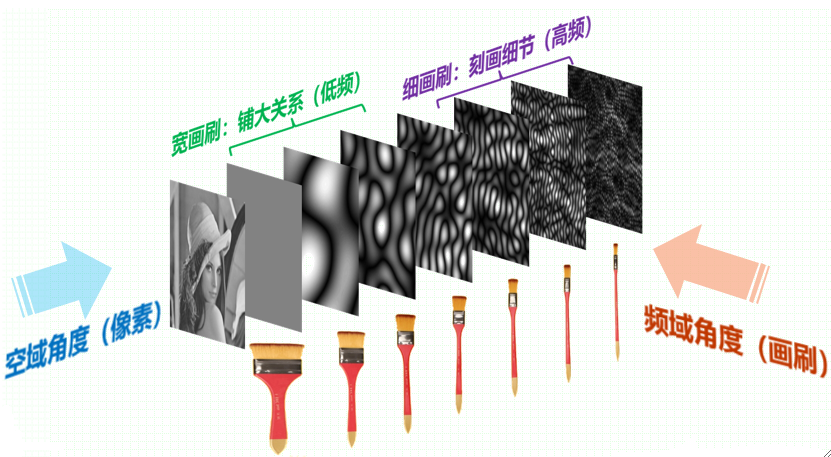
· 通过一个动图可以更清晰直观的看到:
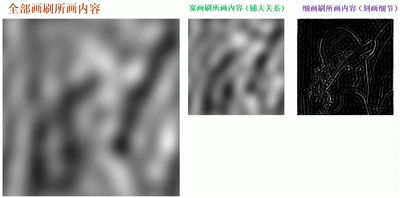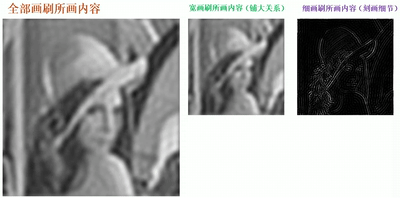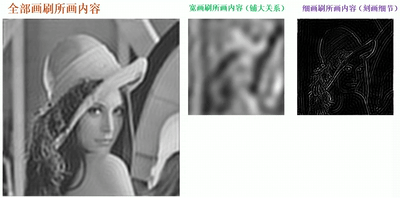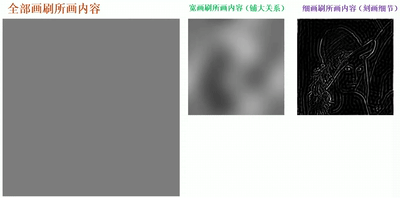
傅里叶变换的性质
可分离性
· 二维DFT可分离为两次一维DFT。
· 尺寸为M*N的函数f(x, y)的DFT可以分解为如下形式:
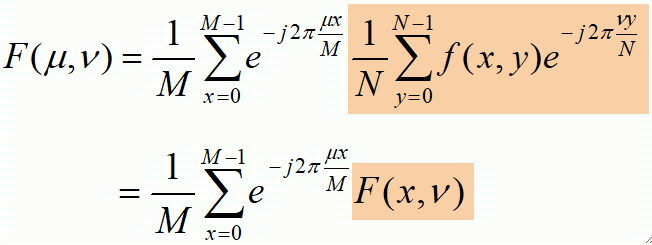
· 其中,F(x, v)是沿着f(x, y)的一列所进行的傅里叶变换,这是内层,外层,沿着f(x, y)的所有列计算傅里叶变换。
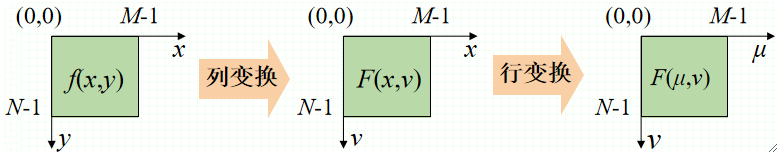
· 在程序实现时,先通过每一列计算一维变换,再通过中间结果的每一行计算一维变换,操作顺序可以改变,即先行后列。
· 同理,可以使用相似过程进行二维傅里叶反变换:
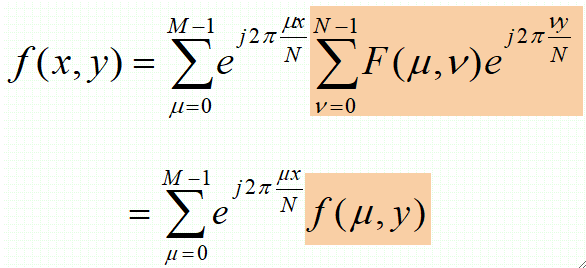
均值性
· 在原点的傅里叶变换即等于图像的平均灰度值。
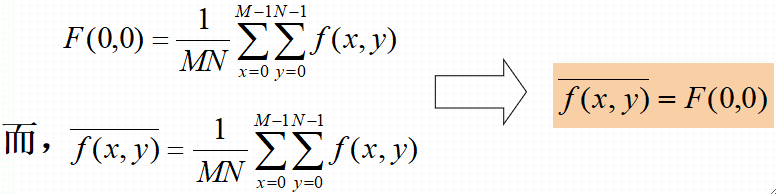
能量守恒定理
· 傅里叶变换前后能量守恒。
· 能量守恒定理也称帕斯维尔(Parseval)定理。
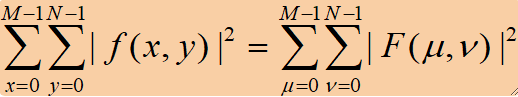
平移性质
· 下列公式表明,将F(μ, v)与一个指数项相乘,就相当于把其变换后的空域中心移动到新的位置。
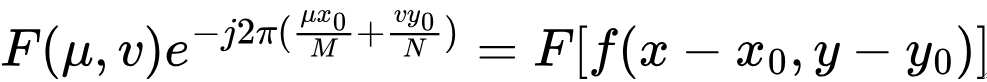
· 下列公式表明,将f(x, y)与一个指数项相乘,就相当于把其变换后的频域中心移动到新的位置。
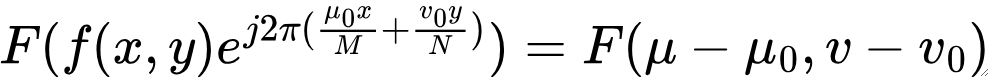
· 由上述公式可知,空域中的图像的平移不影响频谱幅度,即幅值不变,仅对应于频域的相位移动。
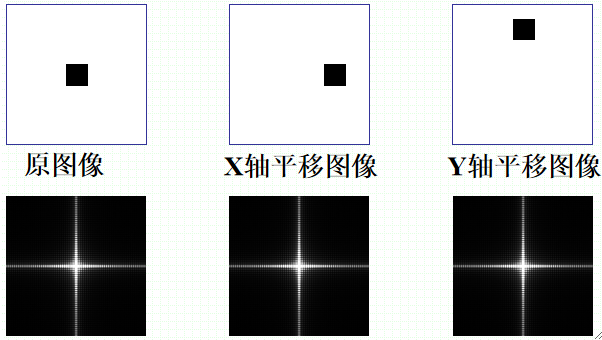
· 根据平移的公式,如果要把频谱的原点移动到矩阵M*N的中心,只需要把μ和v设为M/2和N/2即可。
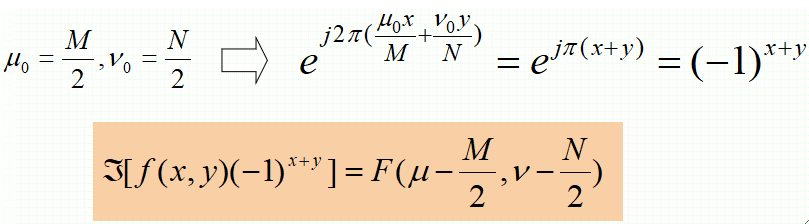
· 即若要将图像的频谱原点移到图像,只要将f(x, y)乘上因子-1^{x+y}后再进行DFT变换即可。

分配律
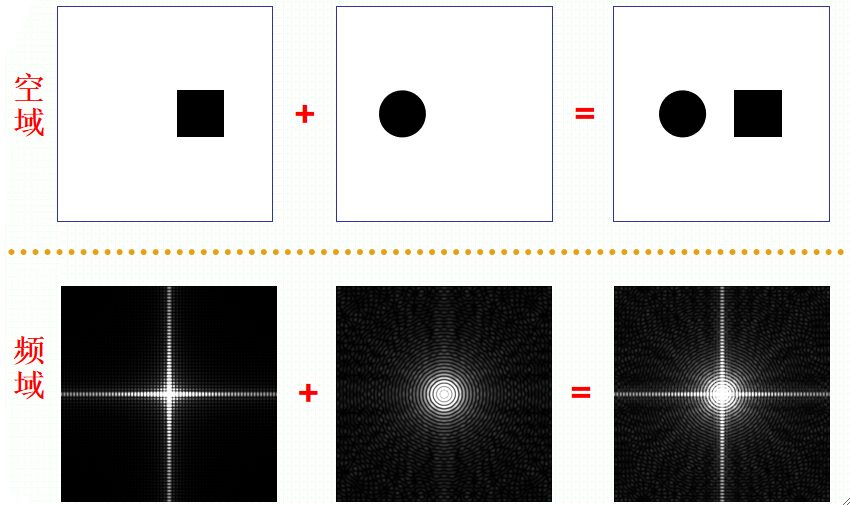
· 傅里叶变换对加法满足分配律,但对乘法不满足。
· 举个例子:
比例变换(尺度变换)
· 给定两个标量α和β,可以证明傅里叶变换对下列两个公式成立:
F[\alpha f(x,y)]=\alpha F(\mu,v)
由该公式和加法分配律可知,傅里叶变换是一个线性变换,有F[\alpha f_1(x,y) + \beta f_2(x,y)] = \alpha F_1(\mu,v) + \beta F_2(\mu,v) 。
F[f(\alpha x, \beta y)] = \frac{1}{|\alpha \beta|} F\left(\frac{\mu}{\alpha}, \frac{v}{\beta}\right)
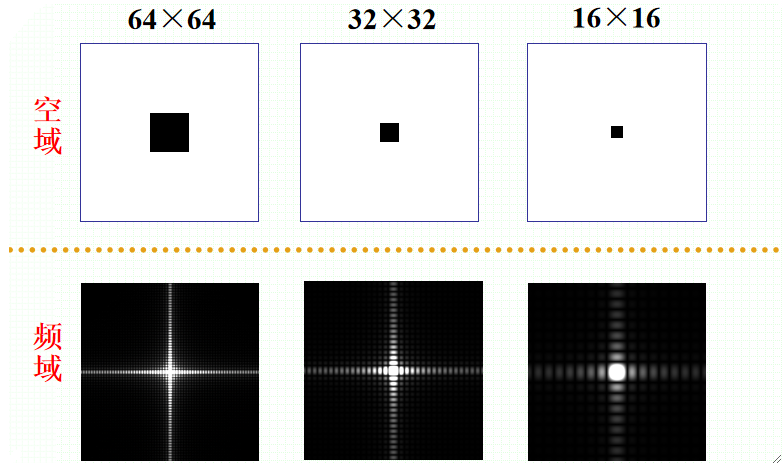
由该公式可知,对f(x, y)在空间尺度的放缩导致其傅里叶变换F(μ, v)在频域尺度相反放缩。
旋转性
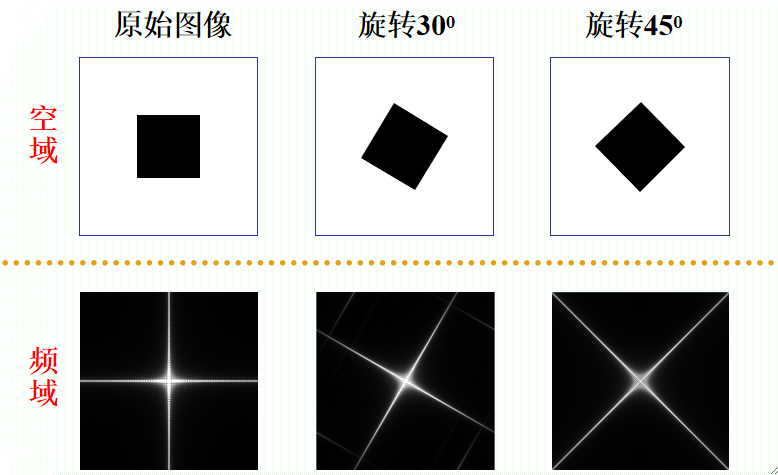
· 对f(x, y)旋转θ度,对应于其傅里叶变换F(μ, v)也旋转θ度。类似地,对F(μ, v)旋转θ度,则其傅里叶反变换f(x, y)也旋转θ。
· 用公式表达如下,先引入极坐标x=rcosθ,y=rsinθ,μ=kcosф,v=ksinф,那么可以把f(x, y)和F(μ, v)转换为f(r, θ)和F(k,ф),将它们代入傅里叶变换有:
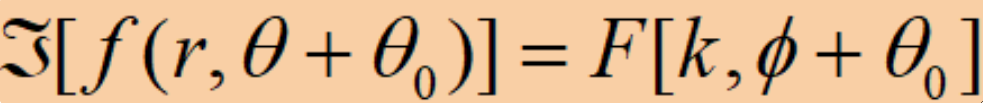
· 举个例子:
周期性
· 只需在一个周期里的变换就可以将F(μ, v)在频域里完全确定。
· 用公式表达如下:
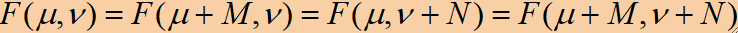
共轭对称性
· 共轭复数:当两个复数实部相等,虚部互为相反数时,这两个复数互为共轭复数。
· 如果f(x, y)是实函数,则它的傅里叶变换具有共轭对称性:
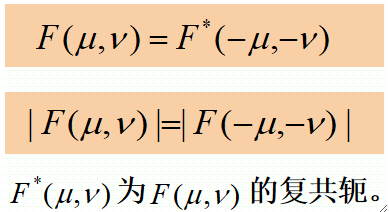
卷积
· 卷积运算是信号处理领域中最重要的运算之一,在众多信号处理领域中卷积和反卷积的问题无处不在。
· 在数字图像处理中,通过卷积模板操作,可以实现图像锐化、平滑等功能。
连续函数卷积的定义
· 对于连续一维函数f_1(x)与f_2(x),它们的卷积定义为:
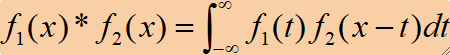
· 对于连续二维函数f_1(x,y)与f_2(x,y),它们的卷积定义为:
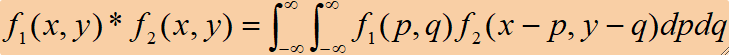
离散一维卷积
· 对于离散序列\{f_1(0),f_1(1),...,f_1(A-1))\}与离散序列\{f_2(0),f_2(1),...,f_2(B-1))\},它们的卷积运算要复杂一些,必须对f_1(x)与f_2(x)的定义域进行扩展,以防止卷积后产生交叠误差(Wrap-around Error)。
· 假设f_1(x)与f_2(x)具有周期M,则卷积结果具有相同的周期。可以证明,只有当M>=A+B-1的时候,卷积周期才不会重叠,才不会产生交叠误差。
· 当M=A+B-1的时候,卷积周期是相邻接的。
· 定义域扩展方法: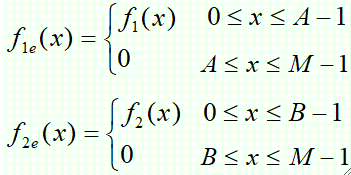
· 有离散一维卷积公式如下:
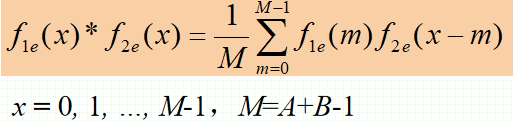
离散二维卷积
· 图像尺寸为A*B的函数f_1(x,y)与尺寸为C*D的函数f_2(x,y)做卷积,也是先扩展定义域:
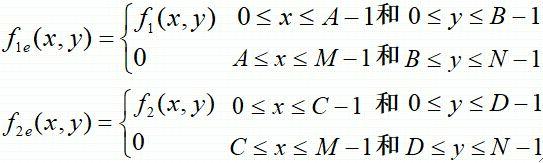
· 有离散二维卷积的公式如下:
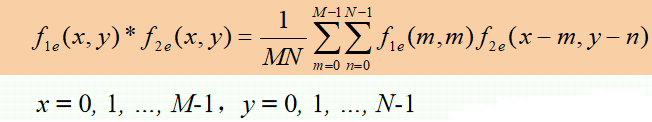
傅里叶变换的卷积定理
· 对于连续和离散卷积都有如下定理成立:
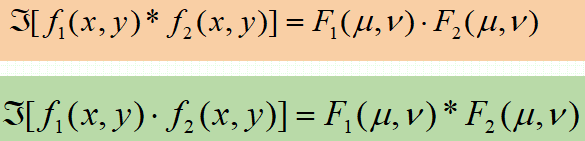
· 卷积是空域滤波和频域滤波之间的纽带。
快速傅里叶变换(FFT)
· 接下来只考虑一维的情况,因为由傅里叶变换的分离性可知,二维傅里叶变换可由2次一维傅里叶变换得到。
为什么需要快速傅里叶变换?
· 从傅里叶变换的公式可以知道,对M个值的每一个都要进行M次复数乘法和M-1次加法,即复数乘法和加法的次数都正比于M^2。
· 而快速傅里叶变换(FFT)只需要做Mlog_2M次,假设M=1024≈1000,则原始算法需要进行10^6次,而FFT只需要进行10^4次,快了100倍!
FFT算法基本思想
· FFT算法基于一个叫做逐次加倍的方法。通过推导将原始M个点的傅里叶变换转换成两个递推公式。
· 首先,假设有8个点,对应函数值为f(0)-f(7),则定义总数M=8,k=M/2=4,将f(0),f(2),f(4),f(6)定义为偶数组,f(1),f(3),f(5),f(7)为奇数组;我们把进行FFT后的基数组记为F(μ),μ=0,1,2,3,偶数组则记为F(μ+k)。
· 然后,我们通过如下递推公式即可顺利算出每个点的值:
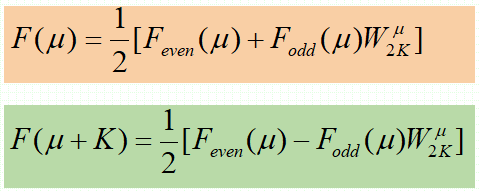
· 可以看到,偶数部分与奇数部分的和可以算出前一半,差可以算出后一半。其中W_M = e^{\frac{-j2\pi}{M}} 。
· 注意M必须满足是2的n次方的形式,如果不满足则需要通过补0来使其变为满足的格式。
FFT算法推导
· (详见PPT,好复杂我不想看了QAQ)
FFT算法举例
· 一维函数的四个采样值为f(0)=2,f(1)=3,f(2)=f(3)=4,计算F值?

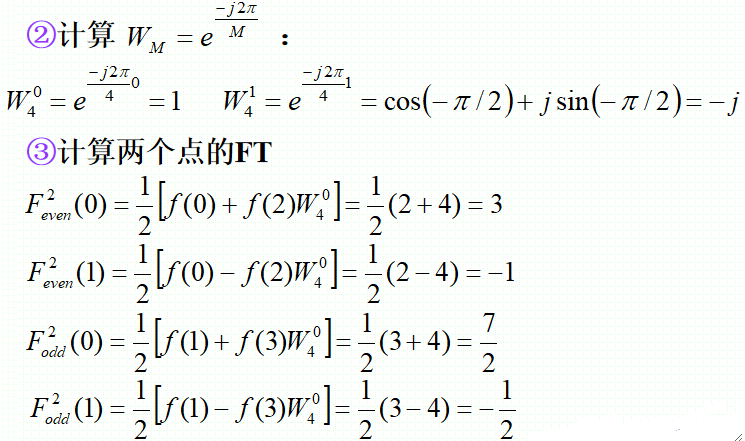

快速傅里叶反变换
· 不需要额外编写代码,我们只需要对正变换的输入一点小小的修改就可用于反变换。
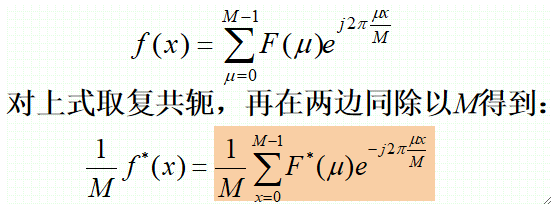
· 上式右边对应一个正变换,把F*(μ)输入一个正变换算法将得到f*(x)/M,因此对上式求复共轭并乘以M就得到所需的反变换f (x)。
