决策树 Decision Tree

决策树作用

· 我们之前学习的算法都是用于连续性的数据的，对于像Excel表格中的离散型的数据，我们没有办法求导，即没办法用我们之前的算法。

· 而决策树就可以作用于离散型数据。

· 接下来我们从一个分类任务，来看决策树。

ID3构建决策树

· 如下表格所示，我们需要做一个二分类任务，即打/不打网球：

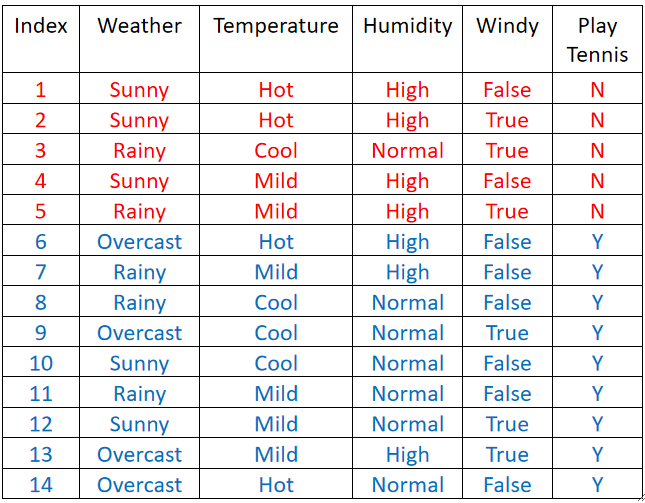
· 假设我们训练好了一个决策树，其实模型本质上就是if-else语句的集合：

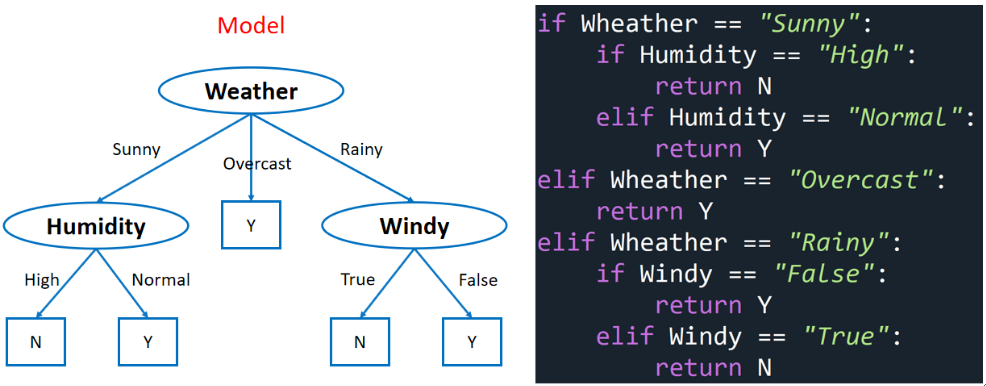
贪心启发式算法

· 构建决策树的时候，我们使用的贪心启发式算法（Greedy Heuristic）就是每次都把所有指标算一遍，选出分的最好的指标作为本次的指标。

· 值得注意的是，因为我们选择的是贪心的算法，所以建出来的树的结果不一定是最好的。

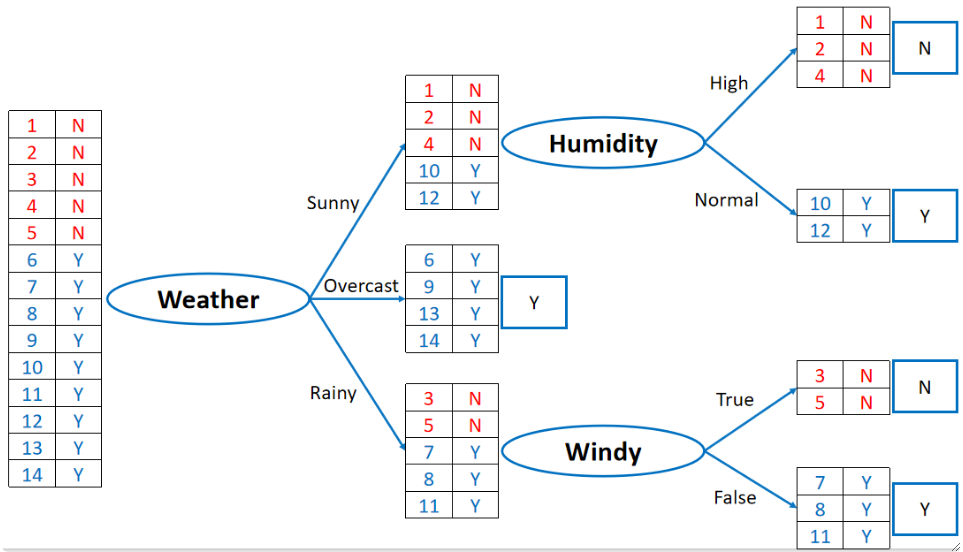
· 如下图，它分的过程是：

1. 在Weather、Humidity、Windy、Temperature中都把所有样本过一次，发现Weather分的最好，因为Overcast分出来的都是Y，然后我们选它作为第一层

2. 然后，对于Sunny之后，我们又跑一次Humidity、Temperature和Windy，跑完之后发现Humidity能分的最好，而且已经能把所有样本都分开了，可以结束；同理Rainy之后又跑一次Humidity、Temperature和Windy，发现Windy分的最好，而且已经能把所有样本都分开来了，可以结束。

   

· 我们引入一个概念——熵（Entropy），用来衡量一个分类结果的不纯度，或者说，不确定性。

惊讶程度（Surprise）

· 在定义熵之前，我们先定义另一个概念——惊讶程度（Surprise）。

· 惊讶程度与事件发生的概率成反比，比如每天都看到太阳从东边升起，惊讶程度低，但如果你看到太阳从西边升起，那惊讶程度就非常高了。

· 用数学公式去定义惊讶程度，其实就是定义一个反比例函数即可：

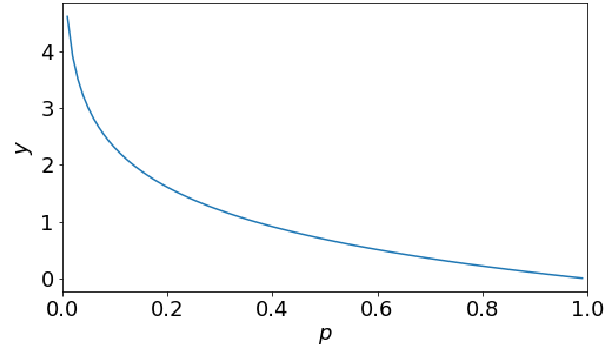
其中P是事件u发生的概率v，画出函数图像如下：

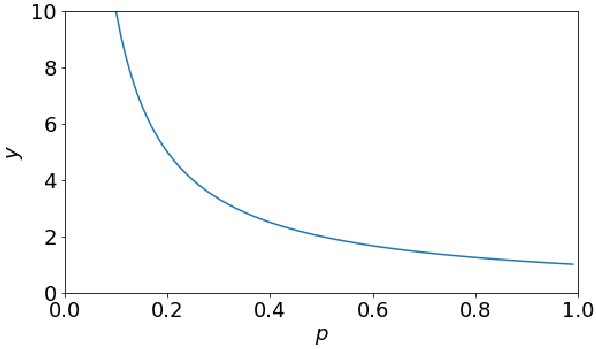
· 但是我们可以发现，当事件的概率是1的时候，惊讶程度也是1，这不是我们所希望的，按理来说是0才比较好。

· 优化一下定义，引入对数，惊讶程度的定义就可以变为：

这样当概率是1的时候，惊讶程度就是0了：

· 一般来说，我们的log都是以2为底的，因为决策树不需要求导，但其实用e也无所谓。

· 有了惊讶程度，我们就可以定义熵了。

熵（Entropy）

· 我们把熵定义为惊讶程度的期望，数学公式如下，其中C为类别的数量：

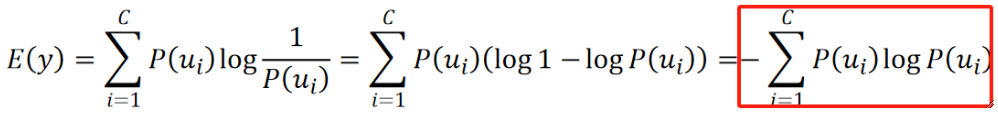
· 举个例子，投一个硬币，出现Head的概率是0.9，出现Tail的概率是0.1，那么：

1. 计算Head和Tail的惊讶程度，代入S=-logP得出Head的惊讶程度是0.15，Tail的是3.32

2. 那么这个事件的熵就是：0.9*0.15+0.1*3.32=0.47

*交叉熵与熵进行比较

· 我们所熟知的交叉熵的定义如下：

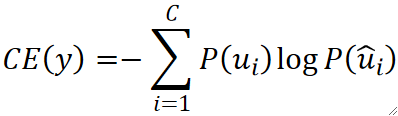
· 其中C是类别的数量，P(u)是标签y，P(u hat)是模型的输出，即预测值。

· 和熵对比，人类很难确切地知道真实概率P(u)，同时，惊讶程度也是一个很主观的概念。

信息增益（Information Gain）

· 我们不能只用熵，而是需要通过信息增益来评价每一个分类的好坏，因为熵只是一个类里面某一组分的好不好，我们需要知道的是整个类分的好不好。

· 我们通过一个例子来看如何计算信息增益：

1. 给出一组数据，N的概率是5/15，Y的概率是9/14，然后我们计算它原本的熵是：

   

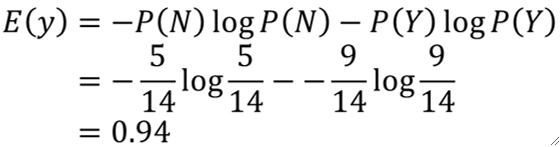
2. 如果我们用Weather去分，可以分成Sunny、Rainy和Overcast三堆。

   

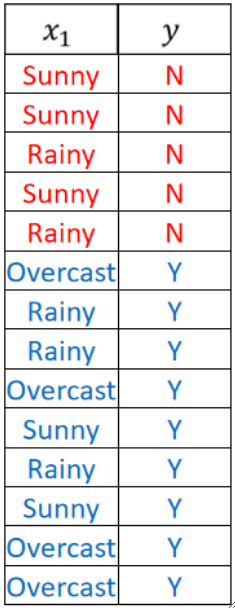
3. 对于Sunny，有5个，其中3个是N，2个是Y，计算Sunny的熵有：

   

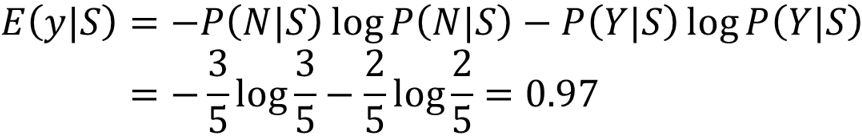
4. 同理，对于Overcast，N有0个，Y有4个，计算Overcast的熵有：

   

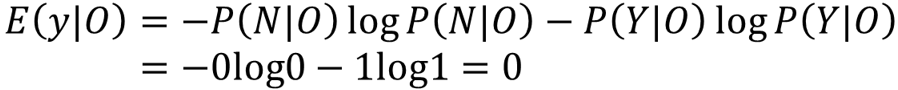
   我们把0log0定义结果为0；其实根本不用算，因为确定Overcast都是Y的，所以熵必为0。

5. 同理，对于Rainy，N有2个，Y有3个，计算其熵为：

   

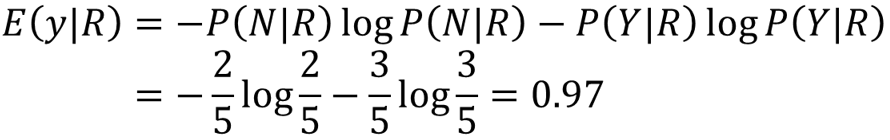
6. 三个都算完了，我们就可以计算信息增益了：

   

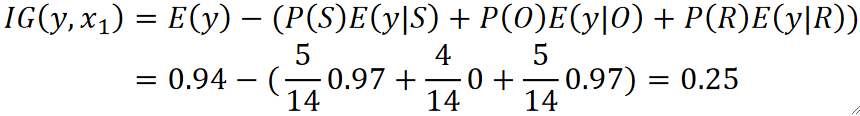
7. 可以看到，其实就是原来的熵减去分完后的熵的期望，我们希望这个值越大越好，因为这代表差距越大，那么熵下降的越多。

8. 最后，我们把剩下的三个特征的IG都算一下，可以发现Weather的是最大的，所以我们第一层就选Weather：

   

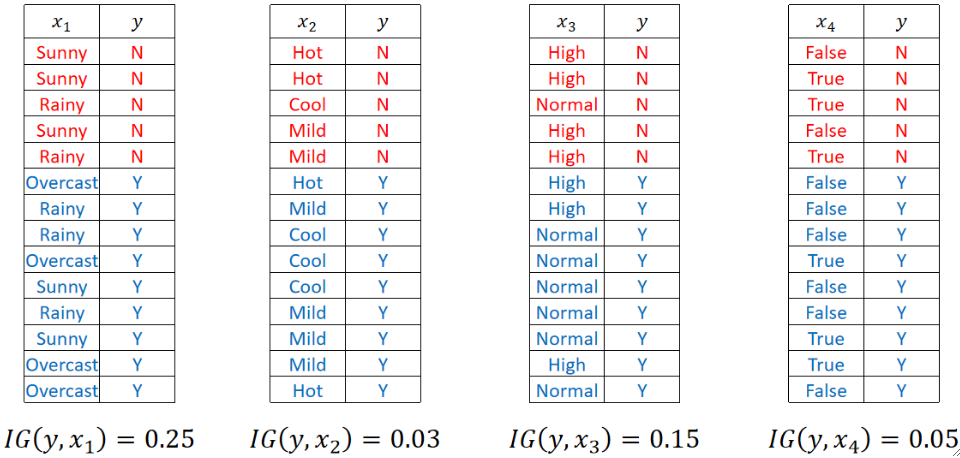
· 我们给这种计算决策树的方法起个名字，叫它ID3。

· 但是ID3这种算法有一些缺点：

1. 如果某一种特征的取值的可能性特别多，那它会更倾向于选这种特征，比如我们把Index，即标号作为特征，因为每一个标号都是唯一的，即可以分出14个组来，每个组只有一个值，这样算出来它的熵就是0，IG就会非常大，那么ID3就会选择它，但很明显我们知道Index这个指标是无意义的。

2. 该算法不支持连续的值（虽然决策树本来就是用来解决离散的值的，但还是想改进一下）

3. 该算法不支持剪枝。

· 因此，C4.5算法就被提出了。

C4.5构建决策树

信息增益比（Infomation Gain Ratio）

· C4.5算法的核心就在于引入了信息增益比，它把信息增益除了一个熵：

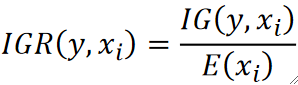
· 这样做有什么好处呢？还是拿上面的例子，如果我要引入Index作为特征，那它算出来的IG会很大，但没关系，它的熵E同样也很大，因为它种类很多：

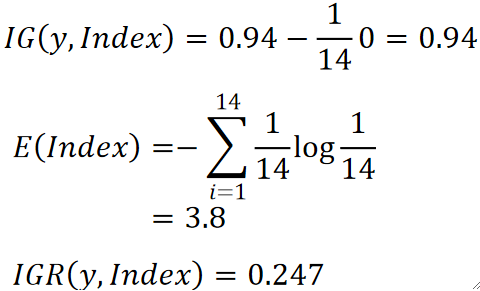
· 这样一除，IGR就会比较小。最后比较这个IGR去选择特征。

连续值

· C4.5还考虑了当值是连续的时候的情况。

· 比如我们的例子中的湿度Humidity，它理论上来说是一个连续的值，假如说数据如下：

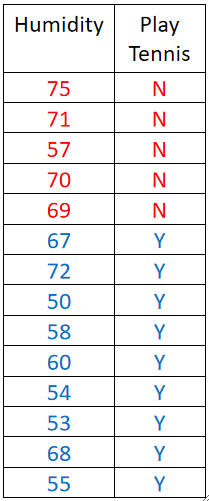
· 首先先给数据排个序，然后依次尝试所有的二元切分，下面展示了三次：

· 假设现在选上了x3作为特征，其分割方式就是大于73.5还是小于73.5，那其实x3在后续还可以继续作为特征，因为小于73.5的时候，还可以再切很多次，考虑很多次这个特征。

· 也就是说，对于这种连续的值，我们可以对其进行复用，因为分完之后还能再分。

· 而离散的值是不能复用的，因为分完之后该组里面这个值就已经确定了，不能再分。

剪枝

· C4.5是支持剪枝的算法。

· 预剪枝（Pre-pruning）：

1. 即边建边剪。

2. 在一开始没有选择任何特征进行分类的时候，根据N和Y的比例进行预测，得出一个准确率。

3. 然后在选择一个特征作为分类节点的时候，再使用一样的验证集进行预测，如果准确率上升了，就继续往后建立节点；如果准确率下降了，那就直接停止，不再建树。

· 后剪枝（Post-pruning）：

1. 即先把树建好，再剪枝。

2. 然后我们使用一个验证集来过一遍树，得出一个准确率。

3. 然后我们开始剪枝，挑选一个节点，把它删掉，然后再过一遍验证集，如果准确率上升了，那就把这个节点剪掉并继续尝试删除其它节点，如果准确率下降了就停止删除节点。

算法特点

· C4.5在连续值上不支持回归。

· C4.5的一个节点可以有多个分支。

· 因此CART算法被提出

CART构建决策树

基尼指数（Gini Index）

· CART算法的特点就在于引入了基尼指数，通过它可以确定一组数据的混乱程度，和熵具有类似的意义，它的计算公式如下：

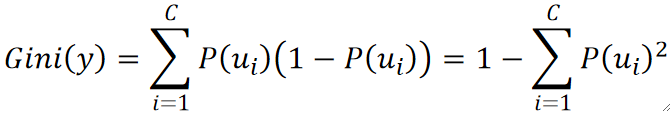
· 比如，对于某个特征y包含14个样本里面有5个N和9个Y，可以算得其基尼指数为：

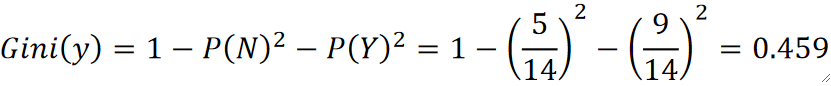
· 如果P(N)=0或P(Y)=0都可以得出y的基尼指数为0，这和熵的结论是一样的。

构建过程

· CART和ID3一样，构建的决策树都是二叉的，不是C4.5那种多叉的。

· 所以对于一个特征内的多个类别，我们只需要分成是或不是该类别即可。

· 我们以刚刚Weather这个特征来举例，他有Sunny、Rainy和Overcast：

1. 先算Sunny的基尼指数，就是算是或不是Sunny，注意要乘上一个期望：

   

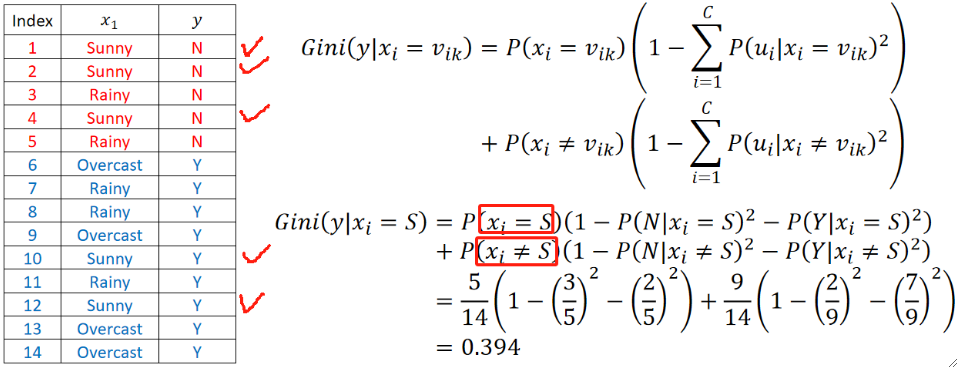
2. 同理，计算Rainy和Overcast的基尼指数：

   

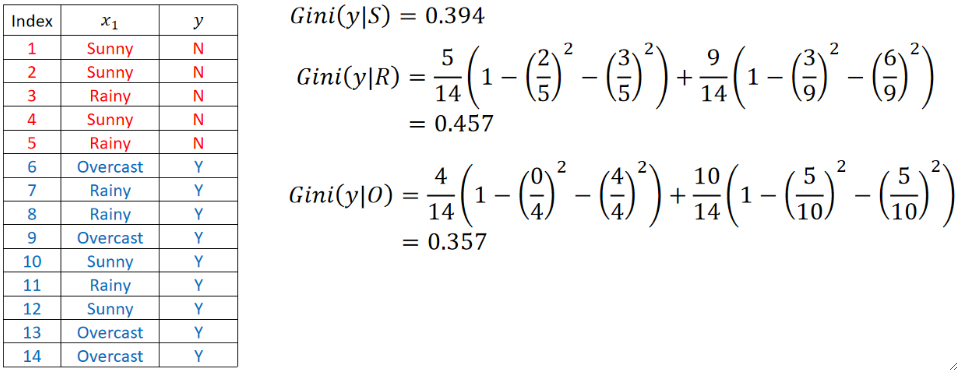
3. 最后，选择基尼指数最小的Overcast作为这一层的分支。也就是一边是“Weather是Overcast”，另外一边是“Weather不是Overcast”。

· 值得注意的是，因为CART只分为两种，所以在“Weather不是Overcast”的下面还可以分“Weather是Sunny”和“Weather是Rainy”，即还是可以复用的！