集成学习 Ensemble Learning

Bagging

· Bagging是一种模型“并联”的方式，如对于一个二分类问题，三个模型ABC得出的结果分别是110，那么根据投票，最终结果应该是1。

· Bagging的全称是Bootstrap AGGregating。其中Bootstrap是一种抽样方式，它是有放回的抽样；Aggreggating指的是类似投票的一个过程。

· Bagging是用来降低高方差的，对于高偏差，Bagging无能为力。

· Bagging是一个框架而不是一个算法，你可以把它套在几乎任何模型的推理上。

工作流程

· 首先，把数据集D根据有放回的随机抽样分出三组数据来，这就是Bootstrap Sampling：

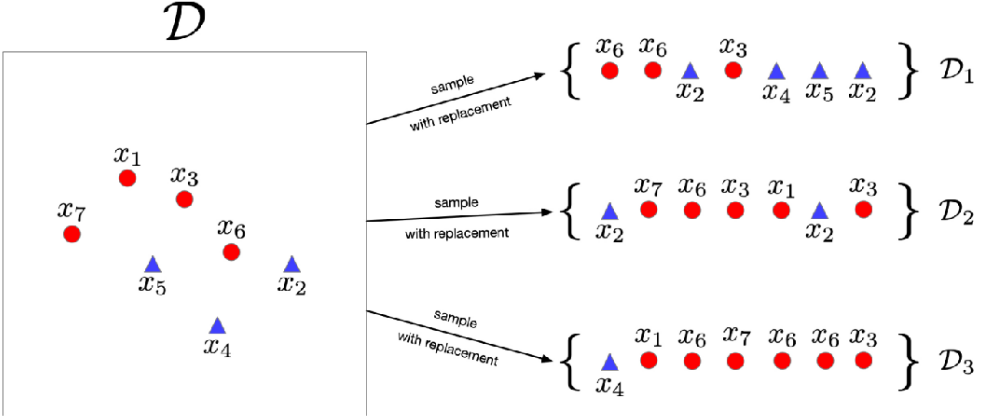
· 其实如果条件许可，采集三组完全不同的数据集是最好的办法，但是数据采集很麻烦，所以只能折中。

· 然后用这三组数据训练三个模型，把它们输出的结果求个均值即可：

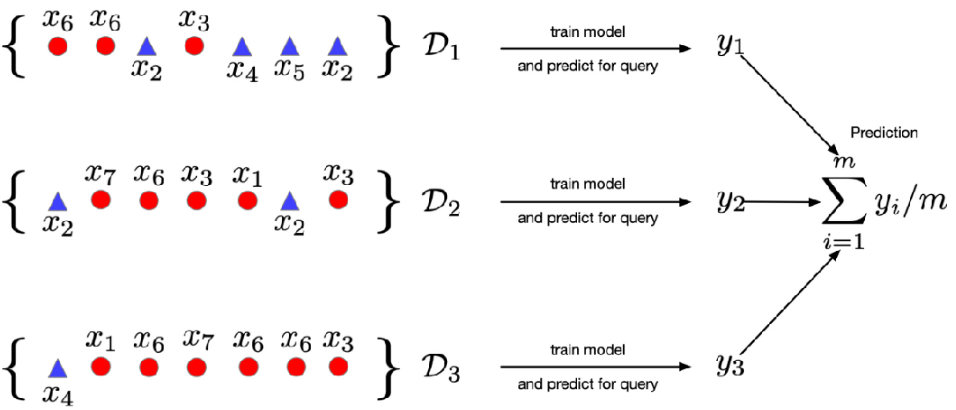
Bagging用在回归任务中

· 其实之前在讲模型的方差和偏差的时候，我们就用多项式回归的例子来介绍过Bagging了：

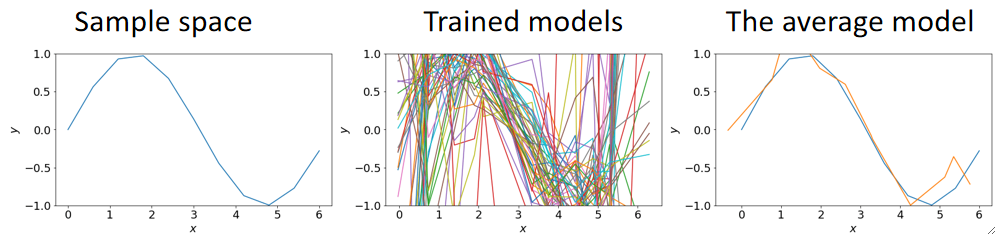
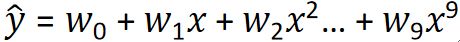
· 可以发现，训练了很多次之后每个模型的方差都很大，但是取一个平均之后，就和真实值非常接近了。

Bagging用在分类任务中

· 加入我们要进行二分类的任务，模型的输出只有0和1，那Bagging其实就是：

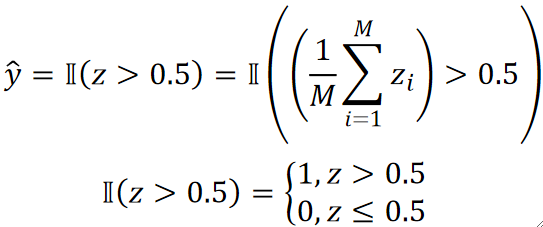
· 举个直观的例子，3个模型，分出的结果是1、1、0，那根据上面的式子，z=(1+1+0)/3>0.5，那么根据指示函数II，它最终y hat就是1。

随机森林（Random Forests）

· 随机森林就是在决策树中做Bagging。

· 在Bootstraping采样点过程中，我们先对行进行采样选出要用的样本，再对列进行采用选出要用的指标，最后通过选出的样本和指标来建树：

· 然后重复这个过程，选出好几组数据和指标来建好几棵树，最后通过这几棵树去做Bagging。

总结

· Bagging在训练多个模型的时候可以进行并行训练，即多个模型一起训练，不分先后，这样速度就很快。

· Bagging只能用于降低高方差，对高偏差没有任何作用。

Boosting

· Boosting是一种模型“串联”的方式。假如有三个模型，它们的运行顺序是1->2->3，即2要等待1的结果，3要等待2的结果。

· 因此，使用Boosting的时候，模型是串行训练的。

· Boosting是用于降低高偏差的，同时也会提高方差。

· Boosting其实就是训练多个弱学习器（Weak Learners），比如先训练1，然后基于1的结果训练2，再基于2的结果训练3。

AdaBoost（Adaptive Boosting）

· 这是一个比较古老的Boosting算法。

· 我们通过下面这个例子来理解AdaBoost。

· 首先，我们可以看到下面的样本是绝对没办法线性可分的，但是我们就想把他用一个简单的模型分开。

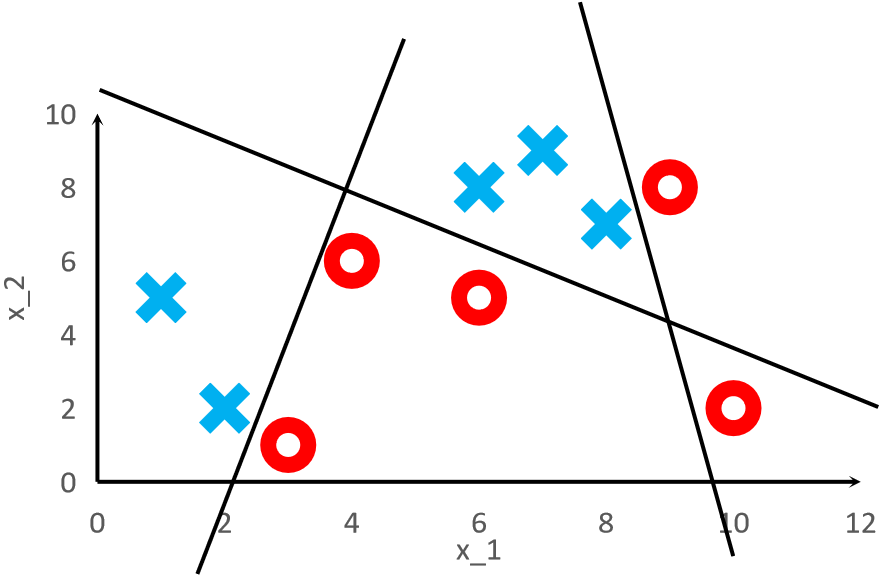
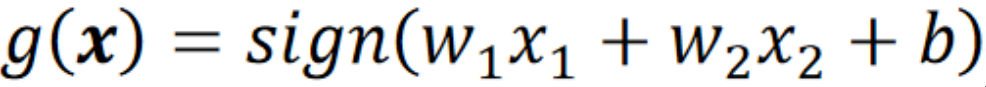
· 可以看到，我们训练了3个模型，并且每个模型是在上一个的基础之上训练的，最终分类的结果可以很好的把所有点都分开。

· 再来看一个例子，我现在模型变得更简单了，只有一条线，训练之后仍可以把点都分开：

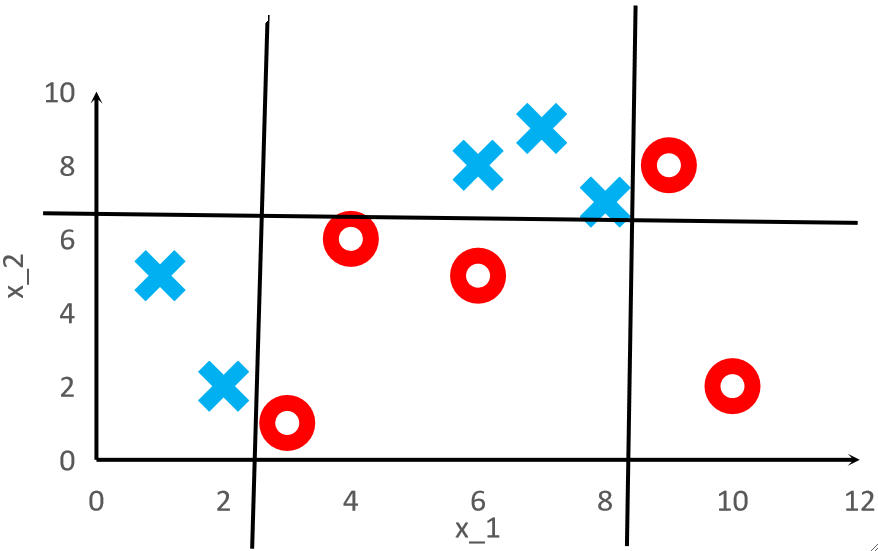
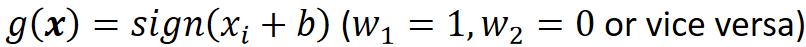
· 可以看到，即便是简单的模型，也可以很好的把复杂的点分开来。

· 我们用一个公式把所有模型的结果结合起来：

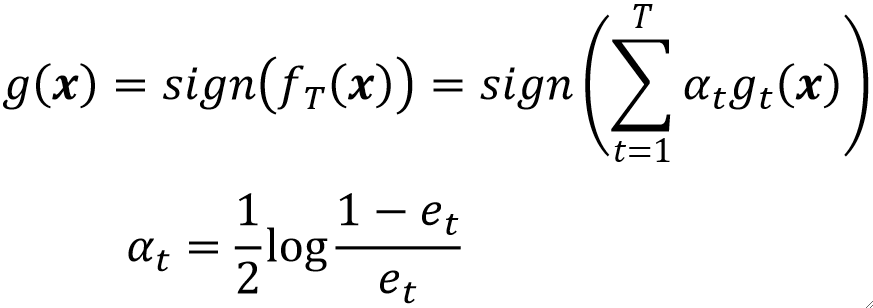
· 可以看到，最终的输出就是每一个模型的结果乘上它的权重然后取符号。

· 这个权重α是可以被直接计算出来的，他和模型的错误率e有关，错误率就是做错了多少，和正确率相反。

· 然后，我们需要规定一个对于f_T(x)的损失函数如下：

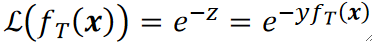
· 我们一步步看这个损失函数是如何规定出来的。

· 首先，我们用正确答案，即标签y去乘了f_T(x)，f_T(x)就是每个模型的输出乘上它的权重（\alpha_1g_1+\alpha_2g_2+\alpha_3g_3），假设我们做二分类，那标签y就只有+1和-1，也就是说，yf_t(x)最后的结果是，如果做对了，那结果就是正的，如果做错了，结果就是负的。而且错的越多，值越大，因为错的越多，f_T(x)就越大，那乘起来的yf_T(x)也就越大。

· 我们用z去代替yf_T(x)，然后画出最后以e为底的图像，即LOSS的图像，如下：

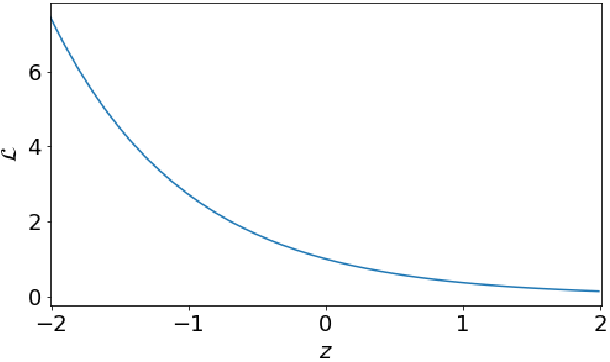
· 可以发现，模型做的越对，即z越大，损失就越少，模型做的越错，即z越小，损失就越多。

· 其实可以发现，我们如果把L展开来，假设是3个模型，其实就是每个模型自己的损失乘在一起：

· 可以发现，从公式上来看，讲道理AdaBoost是可以并行计算的，但很遗憾，后面设计出来的算法只能是串行的。

· 假设我们训练好第一个模型，算出来e^{ya_1g_1}比较大，那我们就接着训练第二个模型，得出新的LOSS为e^{-ya_1g_1-ya_2g_2}发现还是比较大，那就继续训练第三个。也就是说，在训练第N个模型的时候，前面N-1个模型的损失是已经固定的了。

· 有了LOSS就可以写出COST了，注意这个COST的N是样本的数量，也就是说，每一个样本的损失都被所有的模型去衡量，然后把所有的样本的损失加起来。

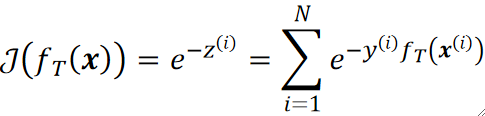
· 接下来我们来推一下为什么每个模型的权重α是固定的。

· 首先我们把COST拆开：

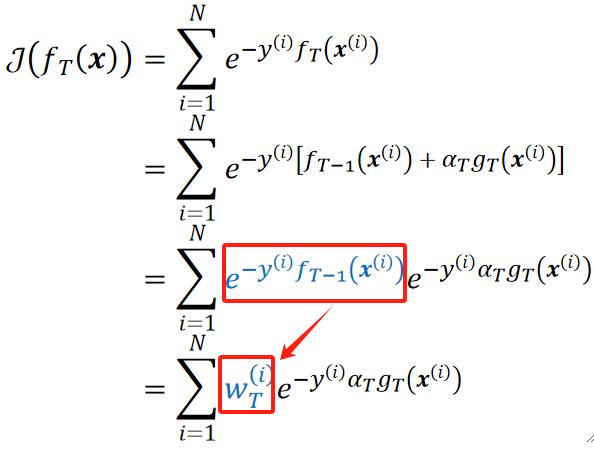
· 蓝色部分其实就是前N-1个模型对第i个样本的损失，根据我们上面所说的，这是已经训练好的了，因此这个值是固定的。

· 然后，我们用w来代替这N-1个模型造成的损失，这就是第N个模型造成损失的重要程度，换句话说，前面N-1个模型造成的损失越大，那么这第N个模型的重要程度就越大，否则就越小。

· 然后我们经过一番推导，最后可以推出来每个模型的权重α的计算公式为：

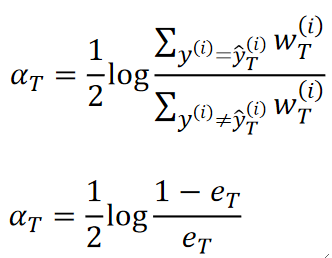
· 其实分子上的准确率，分母上的就是错误率。

AdaBoost训练流程

· 首先，对于n个样本，我们先初始化他们的权重都是1/N，N是样本的数量：

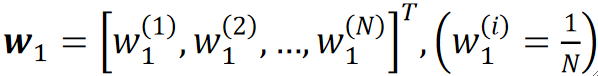
· 然后用这个权重去训练一个弱学习器，计算它的错误率，其实就是错了多少个，就乘多少个1/N：

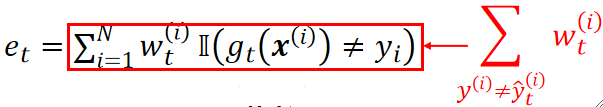
· 然后计算这个弱学习器的权重α：

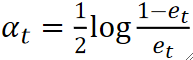
· 然后我们更新下一个弱学习器的权重：

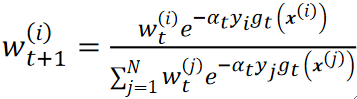
· 从公式中我们可以看到，分子就是这一个弱学习器做的好不好，如果做的好，那下一个弱学习器的权重就下降了；分母就是全部样本的权重的和，也就是说最后算出来的权重不超过1。

· 最后，我们训练了T个弱学习器之后，就可以把这些弱学习器加起来了：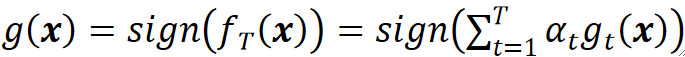

AdaBoost具体例子

· 我们来计算一个具体的例子。

· 首先我们给出x1、x2两个特征，标签y，初始权重w1。训练完第一个模型T1之后得到预测值y hat 1如下表：

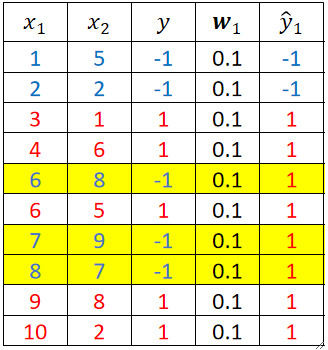
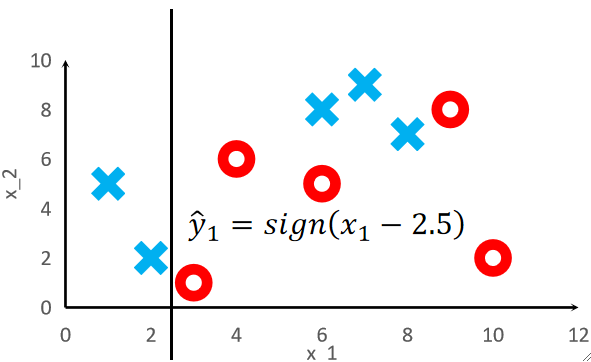
· 很明显这个弱学习器分错了3个点，就是表格内标黄的3个，这样我们就可以计算错误率e1以及这个模型的权重α1：

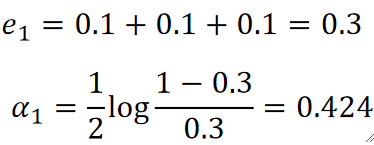
（log以e为底）

· 然后我们就可以计算每一个样本的下一个模型的权重了，这里以做对的第一个和做错的第五个为例：

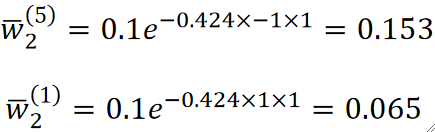
· 然后我们把其它样本都算完，最后得到结果为：

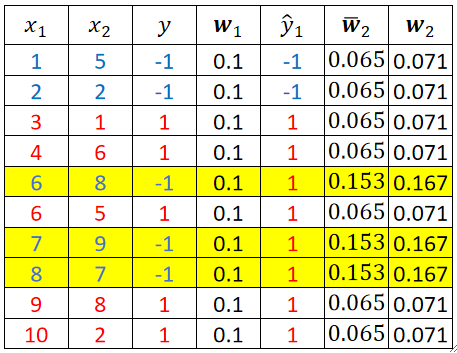
· 注意这里\overline{w_2}是直接算出来的权重，w_2才是归一化之后的权重，算下一个模型的时候我们要使用归一化之后的w_2！

· 然后我们训练第二个模型T2，然后根据它错了几个又可以算错误率和权重α以及第三个模型的权重了：

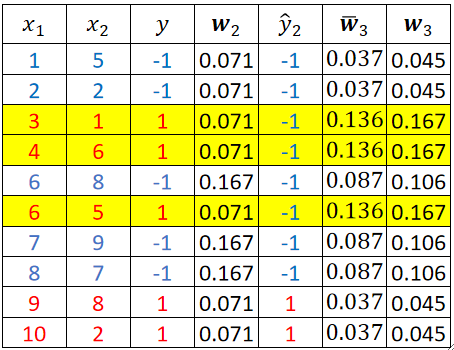
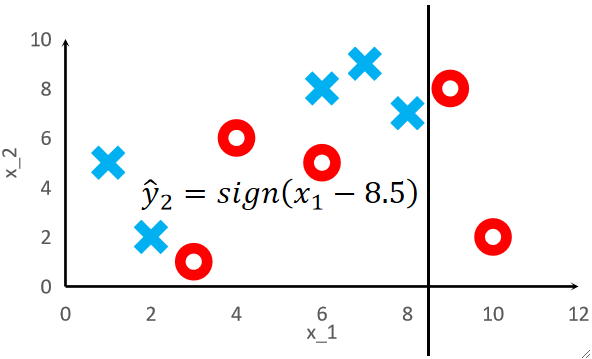
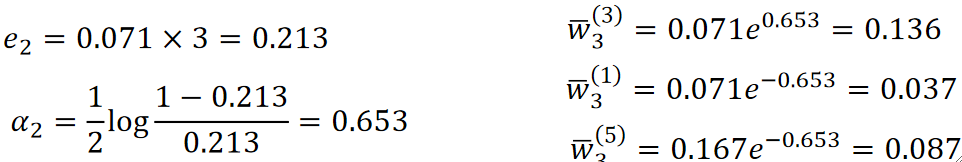
· 然后我们再用第三个权重w3来训练第三个模型，步骤同理：

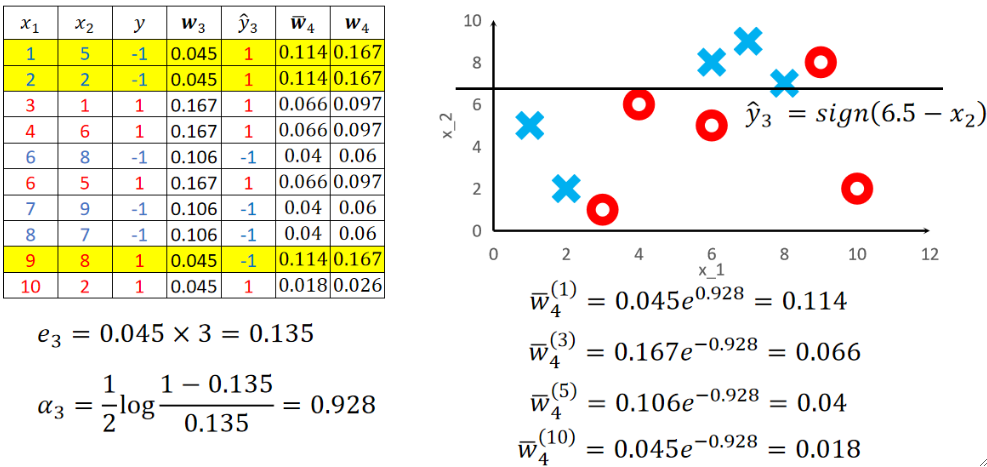
· 假设我们算到第三个就停下来，那最后模型可以表示为：

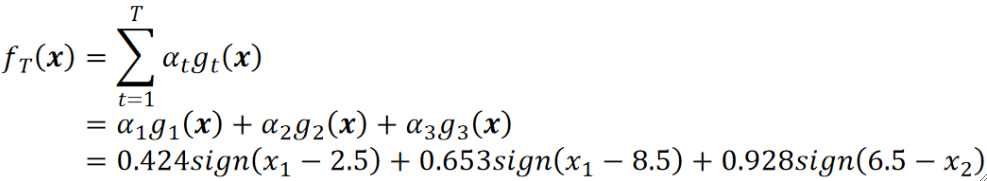
总结

· Bagging：

1. 降低方差；

2. 偏差不改变；

3. 可以并行训练。

· Boosting：

1. 降低偏差；

2. 提高方差；

3. 只能串行训练。