情景引入
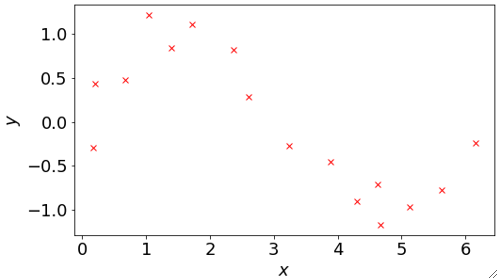
· 首先,我们来考虑这么一个问题,给你一些离散的点如下,要求使用多项式函数(Polynomial Function)做回归预测。
· 多项式函数的表达式如下,我们之前的线性回归和逻辑回归用的就是多项式函数的模型。
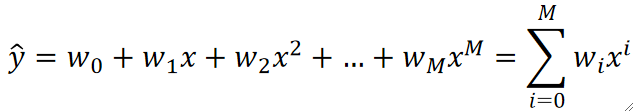
· 值得注意的是,在多项式函数模型中,我们的维度永远为1(D=1),可以看到,虽然有很多个X,但都是同一个X,只是次数不一样。
模型选择
· 接下来我们依次尝试四种多项式函数模型,得到的结果如下:
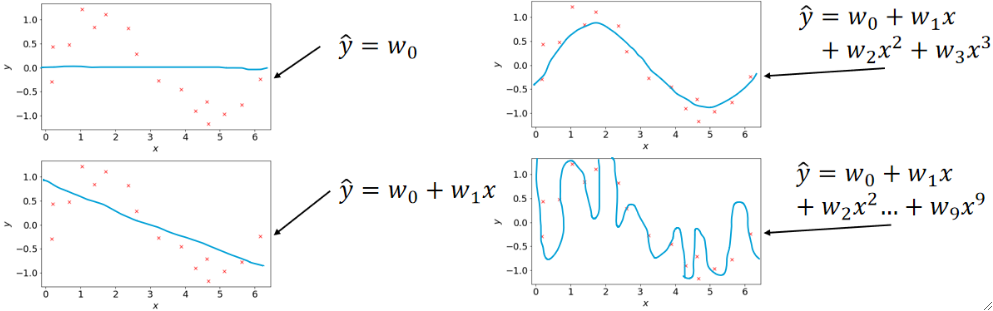
· 不难发现,当选择三个参数的时候(右上角的图)模型的效果是比较好的。
· 还有一个比较奇怪的点是,当我们的参数越来越多的时候,模型的样子就会拐的越来越奇怪。这是为什么呢?
· 来一个比较直观的理解,如果我们选择y=w0的话,理论上我们的模型有∞个选择对吧,那如果我们再引入一个参数w1,那理论上就是∞的基础上再多一个∞,有种无穷的平方的感觉了,既然选择多了,那就意味着能拐弯的地方就多了。这种可能性是爆炸性增长的。
· 对于最后一张图(右下角)它的损失几乎为0,但是这种也是不好的模型,这是因为这个模型的能力很强(可能性很多),所以它在学习的时候,它就很容易把每个数据都拟合上,但是它在对没有数据的地方进行猜测时,就表现出比较差的效果了,因为它能力强,可能性多,能猜到正确答案的几率就更小了,这种模型我们就称之为过拟合(Overfitting),相对的,像左上角这种模型就被称为欠拟合(Underfitting)。
· 解决过拟合的方法很简单,因为它的问题出在猜的地方猜的不好,那我们就不让他猜,把数据尽可能多的给它,这样就能降低猜错的几率了,即继续采样,增大样本量。但是这也是有缺点的,首先收集数据成本很高,其次训练大量数据需要的时间成本也非常高;另一种方案就是选择参数更少,更简单的模型;还有一种方案就是做归一化(Regularization),但这是一种折中的方法,虽然能缓解过拟合,但是会导致偏差(Bias,下面会介绍)上升,这会导致欠拟合。
· 解决欠拟合的方法也很简单,第一种就是换更复杂的模型,即参数更多;第二种就是增加更多的维度(特征),因为过少的特征可能数据没有规律,增加特征可能就会出现一些规律(也很玄学)!
模型评估的方法
· 既然我们知道存在欠拟合和过拟合的情况,那我们就需要设计出一个方法来判断一个模型的良好程度,因为不可能每个模型都把图画出来看,如果是高维的模型甚至都画不出来!
· 我们把收集来的数据分为两部分,一部分是训练集(Training Set),另一部分是验证集(Validation Set),我们用训练集的数据来训练数据,然后用验证集里的数据进行验证,计算LOSS,用LOSS来评估模型的好坏。
· 然后,我们把模型随着迭代的错误率变化画出来,蓝色线代表模型在训练集上的表现,红色线代表模型在测试集上的表现:
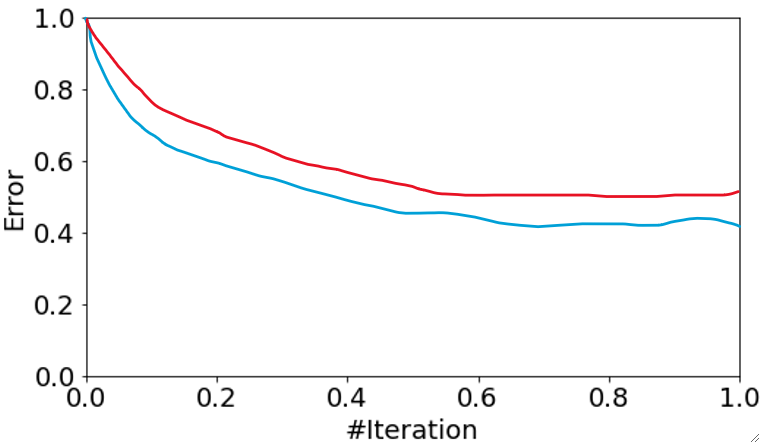
· 不难发现,上面这张图代表的是欠拟合的情况,因为两个准确率都只有50%左右。
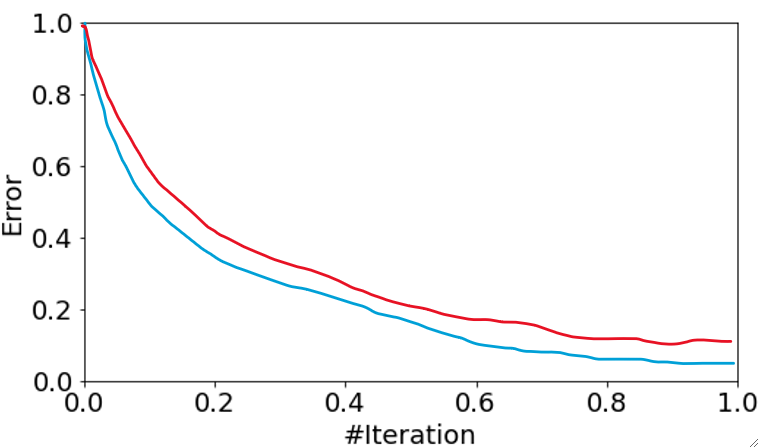
· 这一种就是刚刚好,模型表现得很优秀的情况。
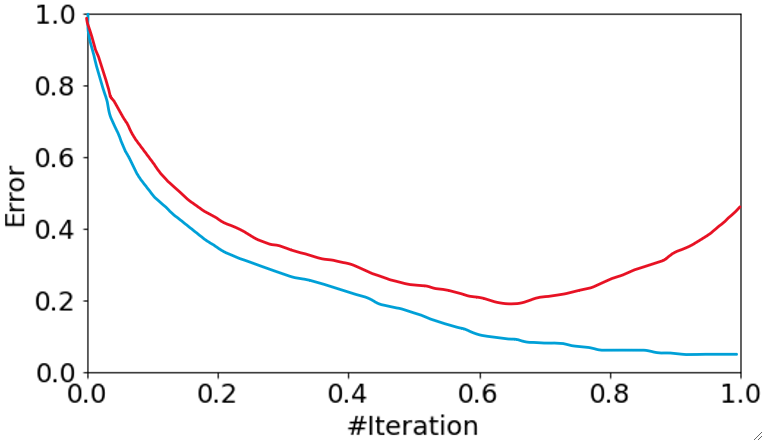
· 最后一种就是过拟合的情况,模型在验证集上的表现先降后升,意味着后面猜的越来越错。
· 不难发现,无论是哪种情况,模型在训练集上的表现一般都会比在验证集上的高,这很正常,可以理解为训练集是练习题,验证集是考试题。
· 其实除了训练集和验证集外,还有一个测试集(Test Set),这个集合一般是拿不到的,可以理解为未来可能会出现的数据,打个比方就是,训练集——练习,验证集——模拟考,测试集——高考。当然,这个集合在我们训练模型的过程中不是必须的,因此可以不用管。
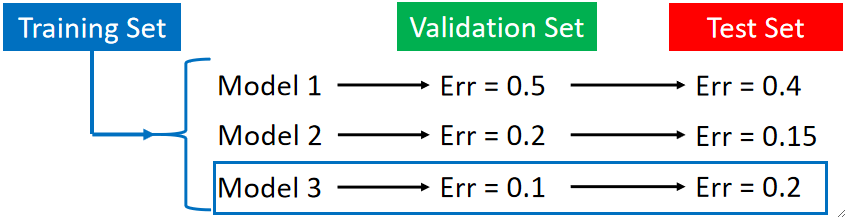
· 因为未来是未知的,所以就有可能存在运气的成分,就好像考试会超常发挥一样,为了排除这个运气成分,选择真正好的模型,我们引入N折交叉验证(N-fold Cross Validation)机制。有了它,就可以从经验上尽量排除运气的成分,注意,不是100%排除,因为运气是永远都存在的。
· 接下来我们就以3折交叉验证来举例,N折就是把一个数据集分为N份的意思,因此我们把这个数据集分为3份。首先,任选一份作为验证集,剩下两份作为训练集,然后用这三份数据去训练和评估已有的模型,得到它们的错误率;然后第二轮,从没被选为验证集的两份中任选一份作为验证集,剩下两份作为训练集,然后拿去训练和评估模型,得到第二组错误率;第三轮,把剩下那份没做过验证集的模型拿去当验证集,其他两个为训练集,然后训练评估,得到第三份错误率。现在,我们对每个模型都有了三份的错误率,然后,对这三份错误率求一个平均值,最后拿这个平均值进行比较,最小的就是最好的模型。
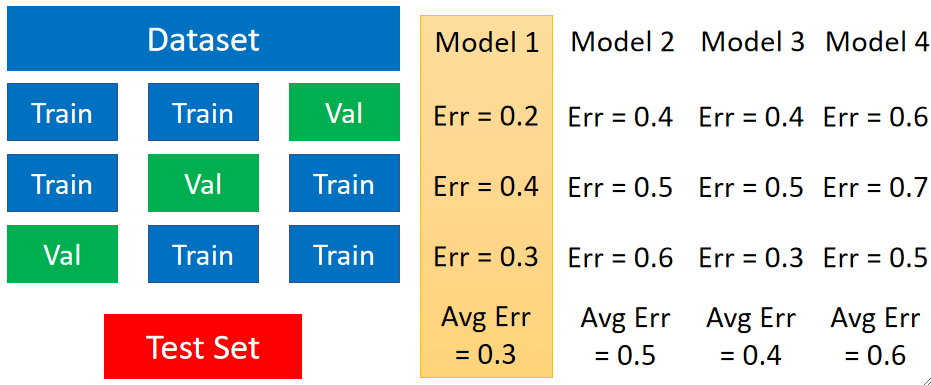
· 一般来说,我们会使用10折交叉验证。但如果数据量特别的大(如深度学习的时候),做10折就会非常消耗时间了,因此5折,3折也是可以接受的。
· 除了选模型之外,在进行N折交叉验证的过程后,我们可以统计这N次之后错误率的偏差(Bias,即与0的距离)与方差(Variance,错误率的聚拢程度),有了这两个数据,我们可以推断出很多信息。
· 观察下图不难发现,随着参数量的增多,N折交叉验证后的结果会呈现的越来越乱,原因也是可能性的爆炸性增加,因此越乱就能说明过拟合,越集中就能说明欠拟合。
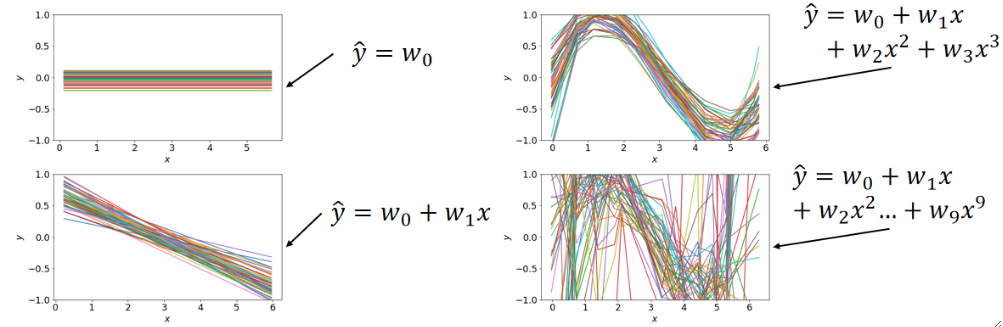
· 在进行N次后我们得到了每一个参数的N个结果,这样我们就可以求一个平均,然后把求平均之后的图画出来:
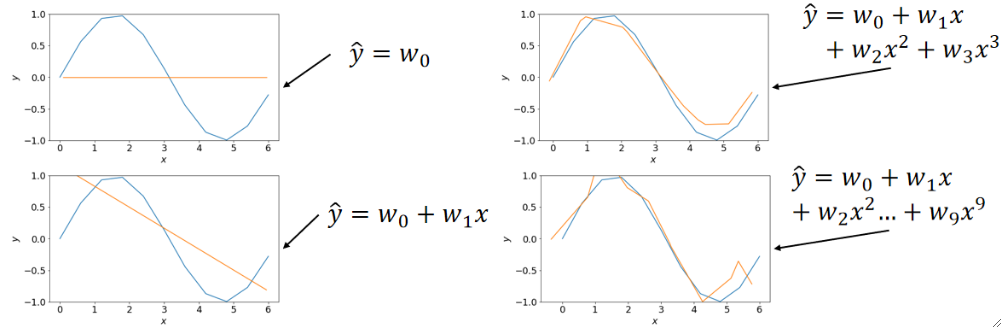
· 很有趣的一点是,在最后一个图中,尽管10条线都很乱,但是求了平均之后的线却是比较美观,比较接近正确答案的!因为尽管每一次都很随机,但是都是围绕着正确答案转的,只要次数够多,求平均之后都能接近正确答案!
· 因此,由偏差和方差我们也能判断欠拟合和过拟合:
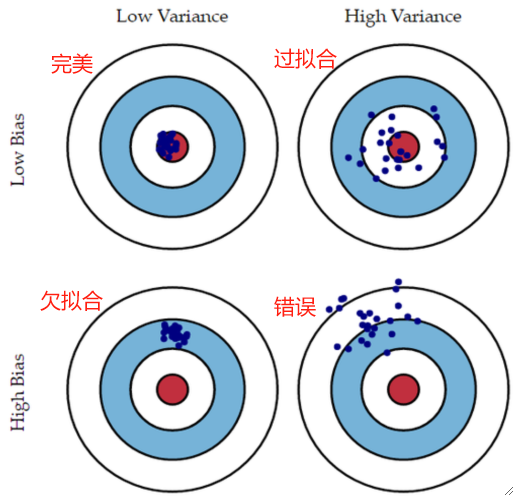
· 可以看出,欠拟合虽然求了平均之后也基本在正确答案的范围,但是随机性太强,方差高;过拟合就是,随机性很少,因此能聚拢,方差小,但是学习能力差,没办法学到正确答案,偏差大。
· 第四种情况其实就是,数据集本身就出错了,学习的过程都是乱来的!
