前言
· 损失函数对模型的表现具有重大的影响,能否规定出一个能准确衡量LOSS的函数至关重要。
· 接下来,我们将以逻辑回归的LOSS函数选定为例,探讨一些有关损失函数选择的思考。
· 我们算出了z的值,但z的的取值范围是R,因此我们的LOSS需要输入一个z,输出一个y hat,不是0就是1。
尝试1——0-1损失
· 这是最直观,最容易想到的方法,即如果z>=0那y hat就是1,否则就为0,表示为:
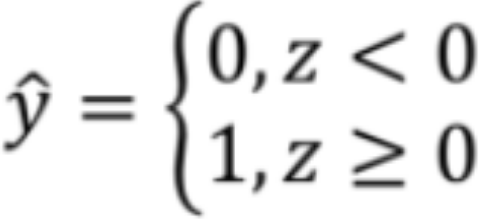
· 这样我们得到了类似Sigmoid的激活函数,那么损失函数就很好定义了,就是直接判断y和y hat是否相等即可:
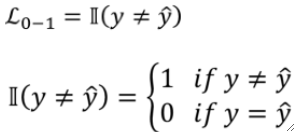
· 小知识,Ⅱ这个符号在机器学习中是指示函数(Indicator Function)的意思,这个指示函数就是用于判断y和y hat是相等。
· 我们来讨论y=1的时候的情况,即y hat=1的时候就猜对了,此时指示函数为0,y hat=0的时候就猜错了,指示函数为1。
· 这样,我们把所有的损失加在一起,就可以数出来错了多少个,这样,错的越多代价就会越高,因此能写出代价函数为:
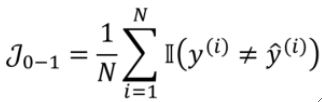
· 这样直觉上来想是没什么问题的对吧,但其实会有一个致命的问题,导数为0。什么意思呢?
· 假设我们现在要对w参数进行优化,那根据梯度下降,我们需要求出w的梯度:
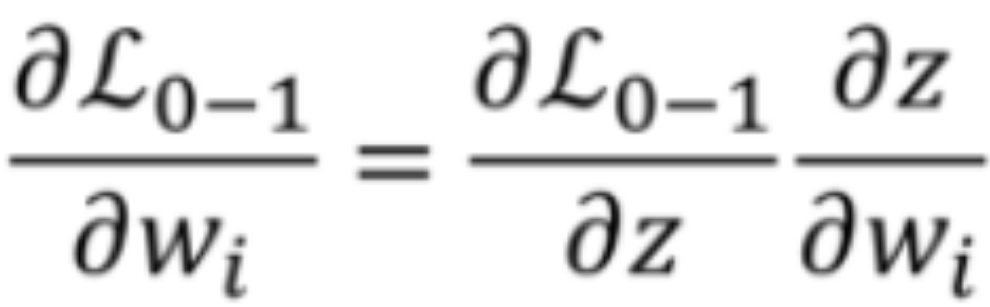
· 我们把z-L的图像画出来看看,z<0的时候L为1,z>=0的时候L为0:
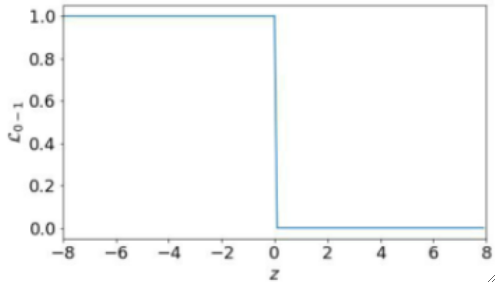
· 很直观了,导数处处都为0,这样就求不出梯度,无法进行优化。
· 这个损失函数最后的结果就是失去了梯度,用人话说就是失去了学习的方向,根本就学不动了!所以这是个失败的损失函数。
尝试2——均方差损失函数
· 我们在线性回归中使用的损失函数就是均方差损失(Squared Error,SE),那套用在这里行不行呢?
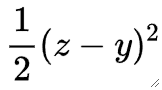
· 同样的,我们把求梯度的时候需要的z-L图像画出来看看(也是讨论y=1的时候):
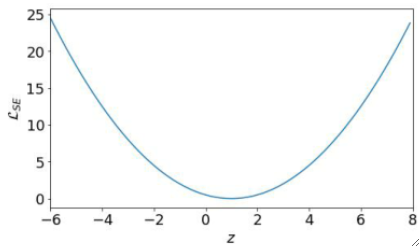
· 很明显是个二次函数,z=1的时候是最低点,然后我们把y=0的时候的曲线也画出来(在z=0的时候最小):
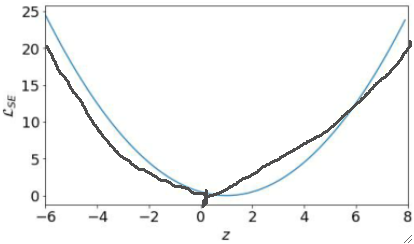
· 可以发现,其实最后我们优化的困难的点只有0到1这一段区间,虽然z的取值范围是R,但是其他值都很容易向0-1靠拢,最后还是要在0-1这段区间里面去优化。
· 这意味着,我们的优化程序需要非常高的精度,因为优化范围只有0-1这一段,这就给我们的优化造成了非常大的阻碍了。
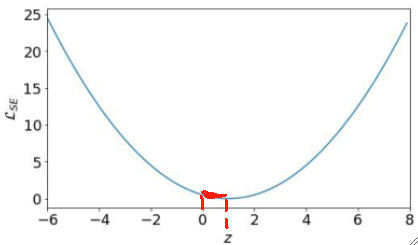
· 理论上来说你硬学是没问题的,但就是有难度,因此这也不是个好的LOSS函数。
· 补充:线性回归不存在这个问题,因为线性回归中的y取值范围也是R。
尝试3——Sigmoid+均方差
· 既然出现了优化范围小的问题,我们就想尝试去解决这个问题,因此我们就提出了Sigmoid激活函数了,它的作用就是把z的取值范围从R映射到[0,1]。
· 然后再套入均方差损失函数,此时就避免了上面我们提到的优化范围很小的问题了,因为映射后的z和y的取值范围一样了。
· 但是这样子就结束了吗?我们还是把z-L图画出来看看,依然是以y=1为例子:
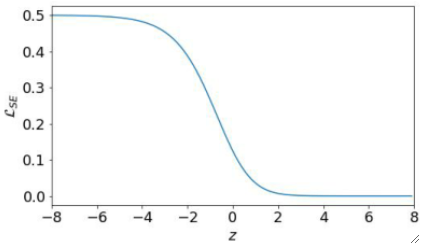
· 可以发现,在z<=-4和z>=4的区间内,L的斜率都几乎为0了,又出现了这种斜率为0的情况,但是有一点不一样。
· z>=4的时候,虽然斜率为0,但是没什么问题,因为此时LOSS也已经接近0了,模型的表现已经很好了,所以即使在这里学不动问题也不大。
· 但是z<=-4的时候问题就很大了,LOSS非常高且梯度几乎为0,这样就是又差又不学了!
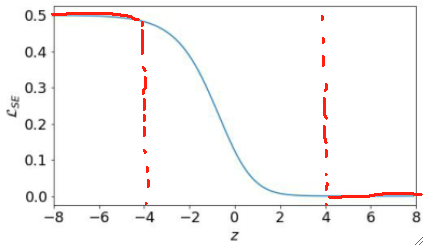
尝试4——Sigmoid+交叉熵
· 一样的,出现了问题我们就要解决问题,我们不希望z-L图的前半段那么平,最好图像就是一直往下的。
· 因此,数学家们就提出了交叉熵损失函数,用这个损失函数就能很完美的解决问题了。
· 画出z-L的图长这样:
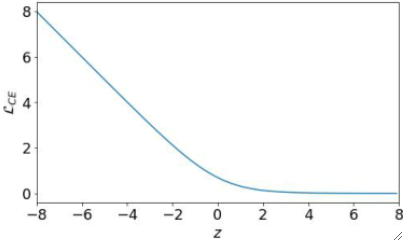
· 可以看到这个函数保证了始终有一个斜率,这样就能保证至少能优化了。
总结
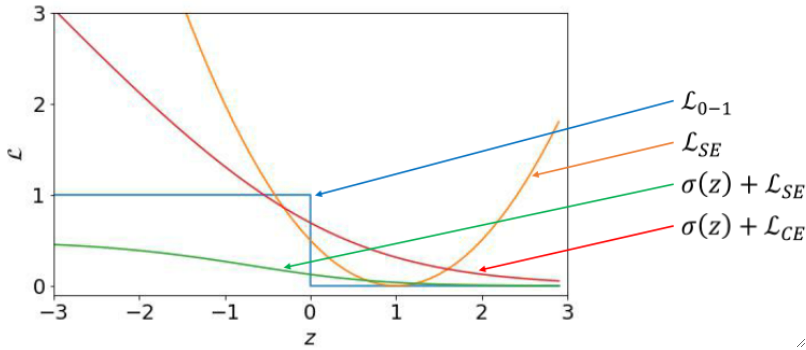
· 我们把刚刚4种尝试中的z-L图画在一张图里,就是: