多分类
· 我们之前使用逻辑回归实现了二分类,接下来我们要进行多分类任务。
· 多分类任务指的是进行2种以上的类别划分,一些典型的运用场景是手写数字识别、邮件类型识别等。
引入
· 我们直接给出一个例子,这个例子有两个特征,三个类别,每个类别有4个样本:
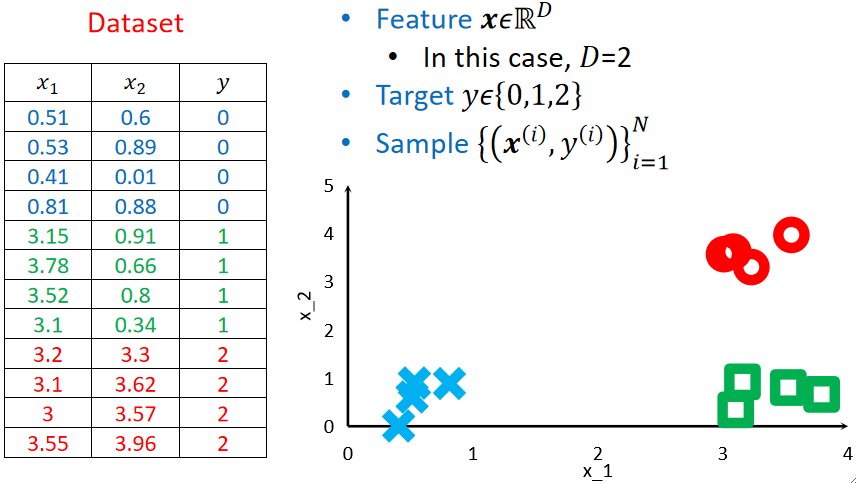
· 可以看到,三个类别分别是0、1、2,但这样子打标签是错误的,为什么呢?因为这存在一个“暗示(Implication)”。
· 如果我们规定了0、1、2,那就暗示了,0到1的距离比0到2的距离要近,换句话说,0和1类别更像一点。如果我们默认了这么一个事情,在计算LOSS的时候就会出问题。举个简单的例子,如果y=0,而我们预测y hat=1和y hat=2的话其实都是错的,但是在计算LOSS的时候,y hat=1的LOSS是1,y hat=2的LOSS是2,也就是y hat=1错的更少一点,y hat=2错的更多一点,这不是我们所希望的,因为他们都是错的,而不存在谁更错!
独热向量(One-hot Vector)
· 为了解决这种暗示的问题,我们引入一个被称为独热向量的机制。
· 直接看图:
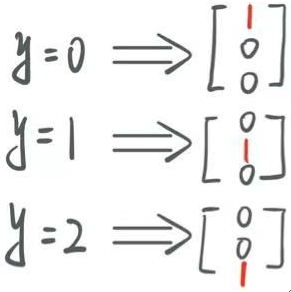
· 可以看到,其实就是有N类别就创建一个包含N个元素的向量,然后,在对应下标处的元素设为1,其他位置设为0。
· 这样只有一个地方为1的向量就被称为独热向量。变成这样的向量,每个类别之间的距离就是一样的了,画出一个三维的图形就可以理解为:
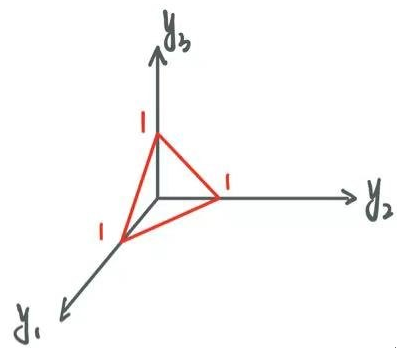
· 除此之外,独热向量还提供了一个信息。举个例子,y=1被转换为了[0, 1, 0],可以理解为,y是第一类和第三类的概率为0,是第二类的概率为1,它表示了一个概率。
Softmax回归
· 在Softmax回归中,我们仍然使用线性模型,但不同的是,我们要使用N个线性模型叠加在一起,即有几个类别就用几个线性模型,以我们上面的例子为例:
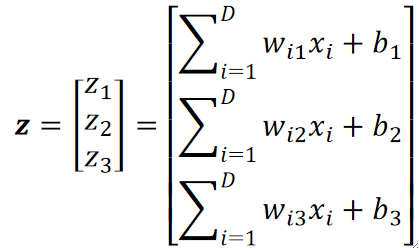
· 最后得到的z包含了三个值,他们代表的意思就是属于第几类的概率。第一个模型算出的z1就是属于第一类的概率,第二个模型算出的z2就是属于第二类的概率,以此类推。值得注意的是,算出的z还不是概率,他是一个属于R的值,后面需要经过一个Softmax函数之后才是概率,但是问题不大,这里也把他理解为对应类别的概率也是没问题的。
· 学出来的模型大概是长这个样子的,其实就是对每一个类别都做一个二分类,比如红色那条线,红色线上面就是”红色类“,红色线下面就是”非红色类”。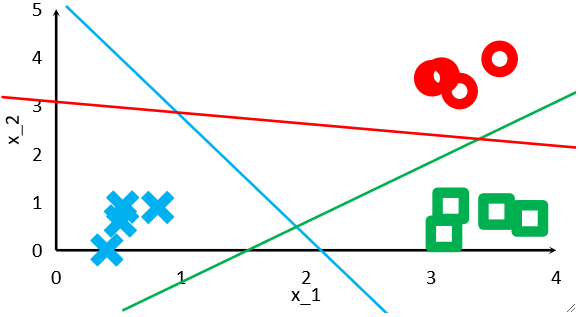
· 然后,假设我们进来一个验证集的数据,它计算出的z的值的结果肯定是红色类的z>0,其他两类的z<0。
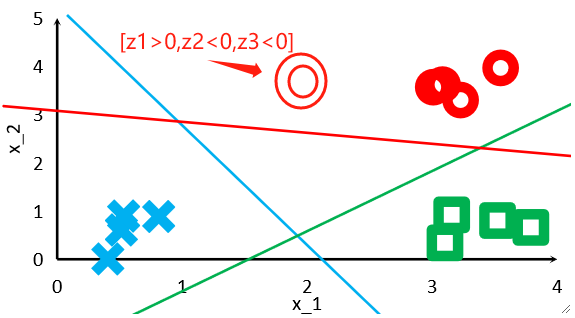
· 到这里其实模型已经可以完成分类任务了,但是还没结束,现在得到的只是z,还不是概率。
· 我们回到公式,我们发现参数w有两个下标,前面的下标指的就是第i个特征的参数,后面的下标就是代表第几类的参数,如wi1就代表第一类的第i个特征的参数。
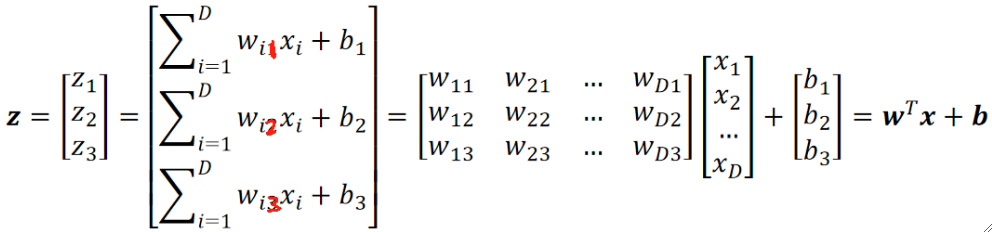
· 接下来就要使用Softmax函数把z转换为概率了。我们需要实现的是,z越大转换出来的概率就越大对吧,因为z>0就是代表它属于那一类,z<0就是不属于。
· 先把函数展示出来:
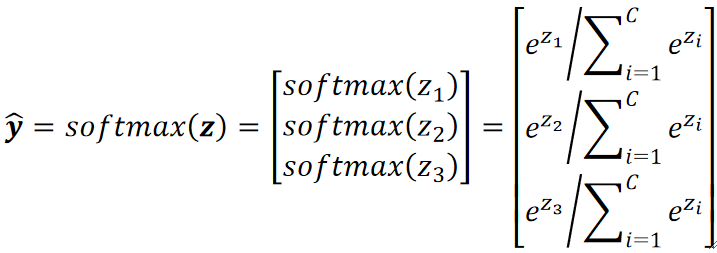
· 首先概率肯定不能是负数,其次,我不希望在转换过程中大小发生变化,如转换前关系是z1>z2>z3,我希望转换后大小关系仍为y1>y2>y3。因此我们使用指数函数把z“抬起来”,就是用e为底即可解决这两个问题。
· 然后,我们要保证所有算出来的y hat值的和要为1,这很简单,让他们分别除以所有y hat的求和即可。
· 到这里Softmax讲完了,说白了其实这个Softmax函数就做了两件事:①让输出变为正。②把输出进行标准化(Normalization),即[0,1]之间,并且和为1。
· 最后把模型表达出来就是:
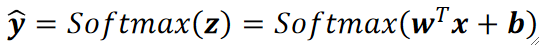
· 可以把Softmax函数看作激活函数,类似逻辑回归中的Sigmoid函数。
交叉熵损失函数
· 模型有了,接下来就要搞损失函数了。
· 之前做二分类的时候我们用的是二元交叉熵损失函数,到了多分类,我们就要使用它的完全体——交叉熵损失函数(Cross Entropy)。
· 它长这个样子:
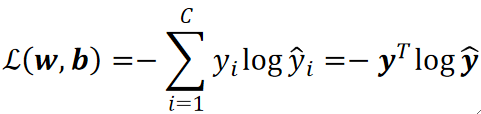
· 其实我们套进去算一次就可以发现,实际要计算的只是-log(y hat)而已,这个y hat就是y为1对应的那个y hat的值。因为根据公式,其他yi都是0,只有目标的那个yi是1。
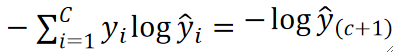
· 把所有损失加在一起就是代价函数了:
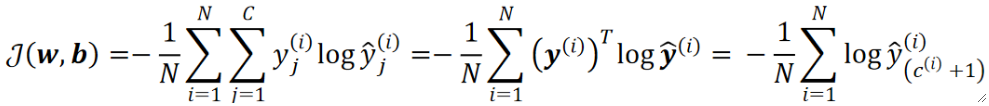
梯度下降计算
· 又到了痛苦的求梯度下降的环节了。
· 还是以我们刚刚的例子为例,把求导过程画出来:
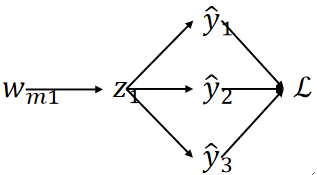
· 接下来就开始求导了:
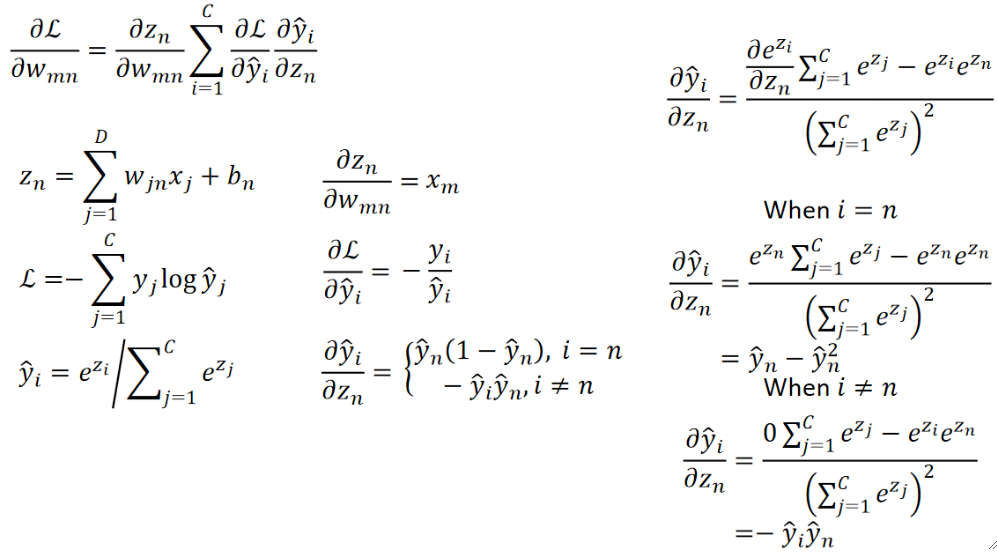
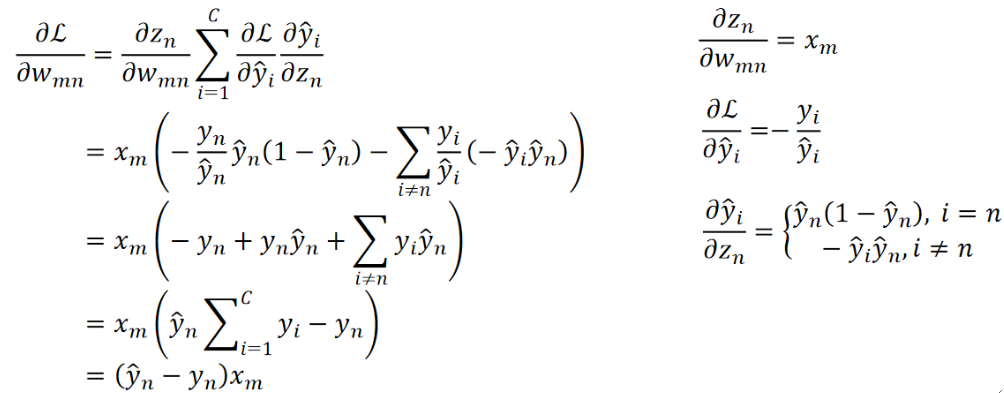
· 算完之后惊讶地发现结果很简单呢!
· 最后来个总结:

K邻近 K Nearest Neighbors
· K邻近(KNN)算法是另外一种多分类算法。
· KNN算法更多属于数据挖掘领域,它不需要模型即可进行训练。
· 参数K是决定测试点考虑K个邻居,最常用的是1-NN,即测试点考虑最近的一个邻居。
· 举个例子,使用1-NN来计算笑脸属于红蓝绿哪一类,那它就会和其他12个元素分别计算一个距离,然后对这个距离排个序,最后把自己归为离自己最近的那一个元素的那一类。
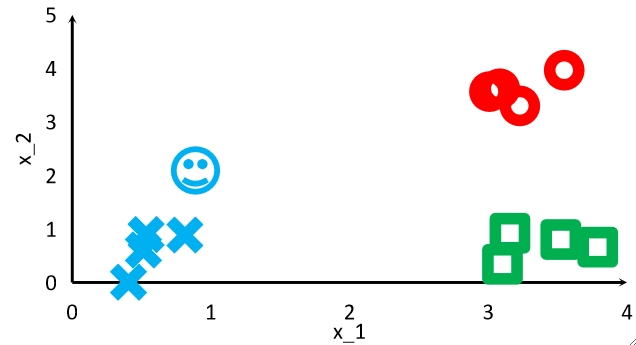
· 这个算法的缺点非常明显:如果数据很多的话,那计算时间就会非常大。
· 再举个例子,如果是3-NN,它也是会对其他12个元素算一个距离,然后排序,然后取前三个,最后把自己归属到这三个最近的元素中占比最高的类里去。
