线性回归 Linear Regression

从房价预测看线性回归

· 首先，我们直接来看一个例子。

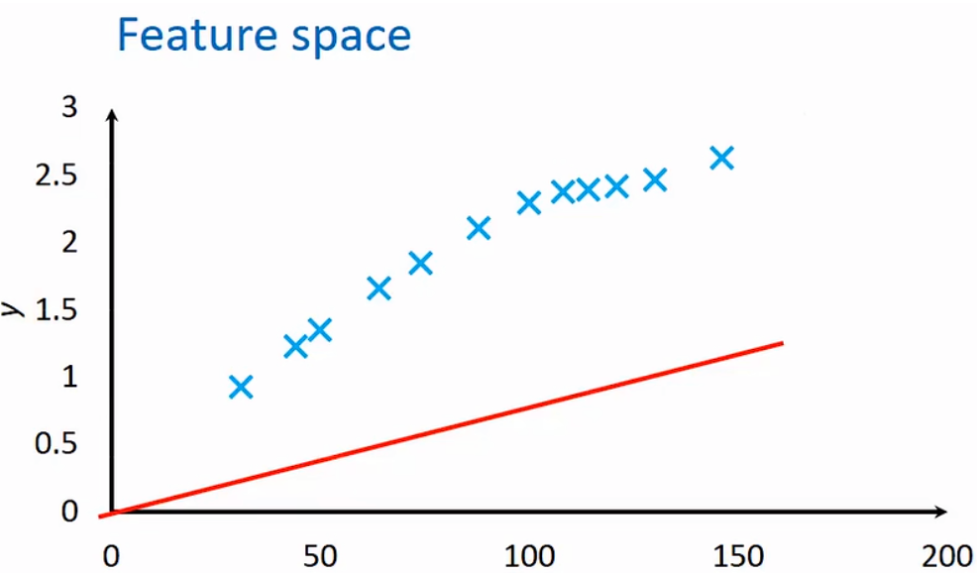
· 现在我收集了某地区房价信息（面积-价格），画成图如下。

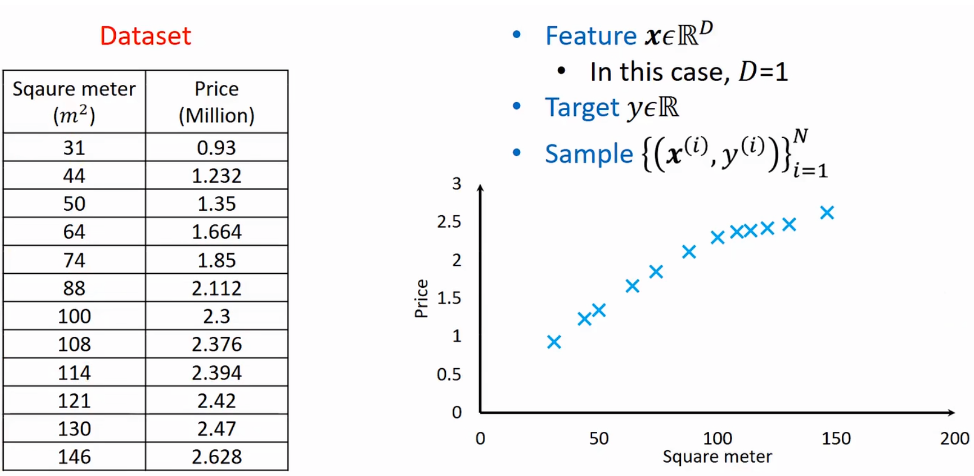
· 现在我希望预测当面积为200平方米的时候的房价是多少。

· 我们知道，机器学习的框架包含了数据集、模型、LOSS和优化，现在我们已经有了数据集。

· 对于这份数据集，很明显输入就是面积，也就是说这里只有一个维度的数据，如果要考虑"地段"这么一个因素的话，那输入就变成了二维的数据。

· 在机器学习中，我们把输入称为特征（Feature），特征都会有纬度D，此处例子D=1。

· 我们把一组数据，即输入与答案，称为一个样本（Sample），在该例子中，一个（面积，房价）就是一个样本。

· 接下来，我们就要考虑模型（函数）了，在这个例子里面，我们可以一眼看出数据是保持一个上升趋势的，所以此处我们用经验选择线性模型（y=wx+b）。

线性回归模型

· 线性回归（Linear Regression），给出其数学定义式如下

·首先，y头上带一个尖角符号用于表示该函数是预测（Prediction）函数，读作y hat，目的是与正确答案y进行区分。

· 然后看函数本身，首先是对wixi进行从1～D的求和，意思是如果考虑多个维度，就要把所有维度的值都加起来，在房价预测中，我们只有一个维度，因此只需要考虑w1x1即可。

·  w是权重（Weights）的意思，但本质上它就是一个斜率。

· b就是截距了，或者说偏移量（Bias）。

· 可以发现这个函数还有另一种写法，因为我们的数据都是用矩阵的形式进行存储运算，所以我们就用矩阵的形式来表达函数。

· 首先，w是一个n*1的矩阵，每一行存储一个维度的w；x也是一个n*1的矩阵，每一行存储一个维度的x；然后把w进行转置，它就变成了一个1*n的矩阵，再把转置后的w与x进行矩阵乘法，得到的就是一个1*1的矩阵，其实就是第一种表达方式了。

· 很明显，y hat和w都是可以取任意实数的。

补充：何为线性？

· 用人话来说，线性在几何上表示其实就是直的、平的、不拐弯的。

· 例如在一维的线性函数是一条直线，二维的线性函数是一个平面。

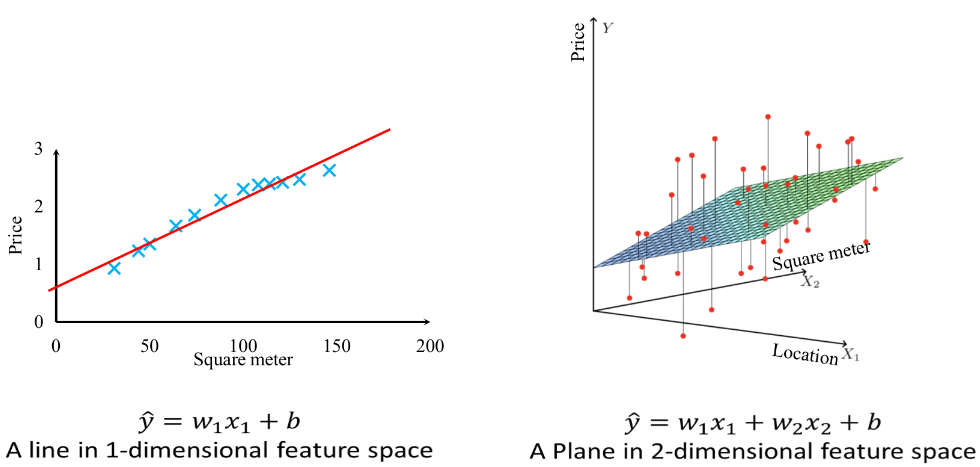
·如果维度再高一维，那我们就没有办法画出来了，我们把三维或以上的图形统称为超平面（Hyperplane）。

线性回归的损失函数

· 有了数据和模型，接下来就要判定拟合出来的线哪条更好了，那就需要用到LOSS函数了。

· 我们使用均方误差（Mean Squared Error）作为损失函数，形式如下

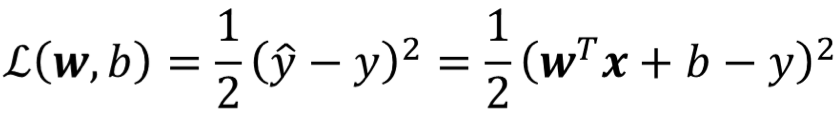
· 从公式可以看出，该函数是用来衡量某一个样本的，而不是整体！

· 衡量的方式也很简单粗暴，就是直接把预测值和实际值相减（y hat - y），那么为什么要加一个平方在外面呢？这是为了消除负数的影响，因为我们衡量这个样本预测的好坏，只有"好"与"不好"两个结果，"好"的意思就是差越接近0越好，"不好"的意思就是差越大于0越好，但如果来了个负数就需要多考虑一种情况，这非常麻烦，因此我们使用平方来消除负数的影响。

· 这个时候你可能会问，为什么不去用绝对值而要用平方来消除负数的影响呢？因为绝对值不好求导！如果要对绝对值进行求导，那就需要进行分类讨论，这也很麻烦，因此我们选择使用平方。这样前面为什么加了个1/2也很明显了，就是为了求导方便。

· 损失函数是用来衡量某一个样本的，但是我们肯定是需要知道整体的表现，因此就引出了代价函数（Cost Function）。

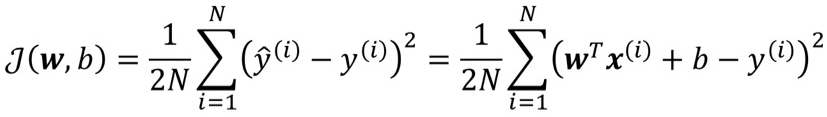
· 代价函数是用来衡量所有样本的整体平均表现的，可以看到它在求和完成之后还多除了一个N，就是为了获得平均表现。

· 其实除这个N还有一个原因，首先我们要明确，不是样本越多训练效果越好，也不是样本越少训练效果越差，但当我们样本多的时候，COST函数铁定会越来越大，如果这个时候不求平均，那样本多的COST大，样本少的COST小，这样比较就不公平了。

· 注意，在很多地方代价函数和损失函数没有非常严格的区分，因此其他地方看到两个概念互相混淆也不要惊奇。

· 很明显，LOSS函数比COST函数更重要，因为LOSS是用来界定好与不好的，它决定了最终把哪个函数选出来，而COST只是简单的求和求平均而已。

优化算法

梯度下降（Gradient Descent）

· 现在我们已经把训练模型的三个要素都集齐了（数据、模型、评估），现在只需要随机无数条函数，算它们的LOSS，找到LOSS最小那个即可，可这并不优雅，并且效率非常低下，因此，我们不得不寻找一个优化算法，让训练又快又好。

· 在讲优化算法之前，我们需要先复习一些数学知识。

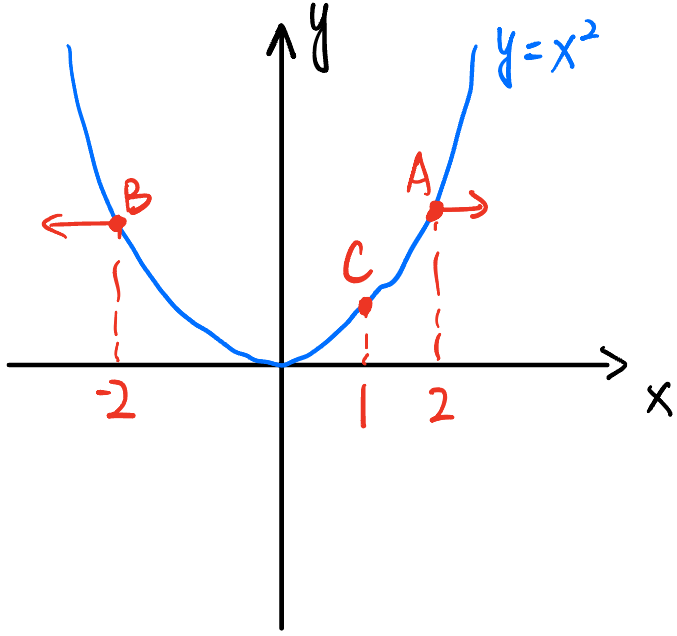
· 首先，我们知道导数是没有方向的，但是，为了我们计算方便，我们现在给导数定义一个方向，我们定义X轴的正方形为导数的正值，反方向为负值。如下图的函数A点的导数值为+4，B点的导数值为-4。

· 有了导数，它可以给我们提供两个信息

① 该往哪边走。很明显，如果A点想要靠近最小值点，要往左走，B要往右走，这就和它们的导数的方向相反。

② 应该走多少。很明显，A的导数值比C的导数值大，同样是想到达最低点，A要走的肯定比C要走的多。

· 接下来上点难度，我们考虑如下三维函数，但为了计算方便，我们把视角调节成从y轴往下看，即第二个图。

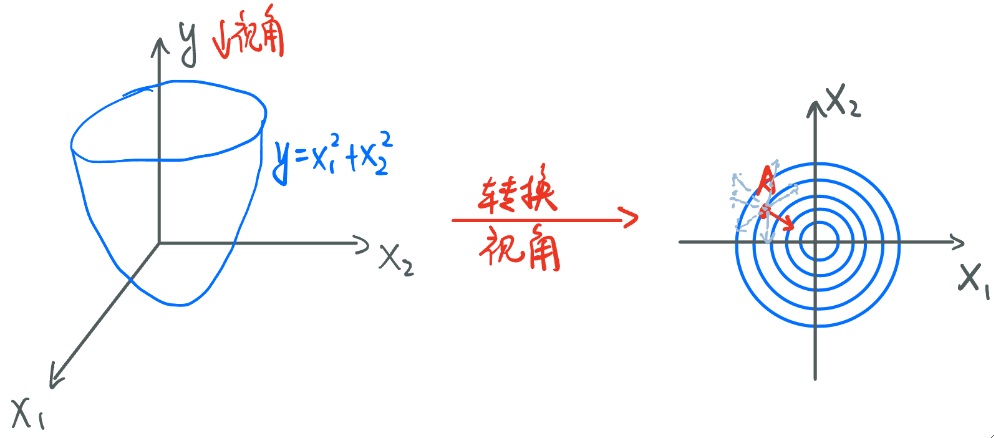
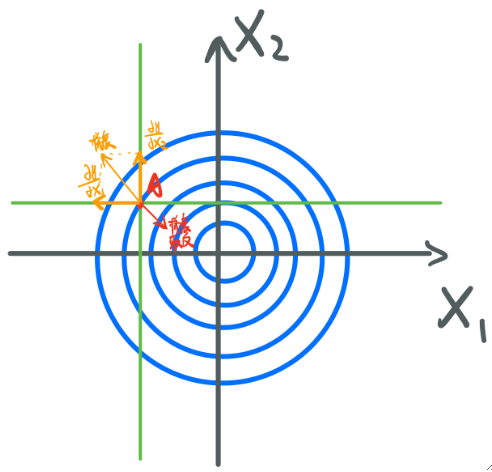
· 现在有一个点A，它的导数因为在三维空间上，因此会有无数个（周围一个圆），我们称之为方向导数。但是，我们希望找到能最快地靠近最小值点的那一个，毫无疑问只能是图中红色方向的导数，我们把这个导数称为梯度（Gradient）。

· 梯度的计算方式也非常简单，对X1求偏导，再对X2求偏导，它们的和就是梯度。

· 那如果遇到了下面的函数，阁下又该如何应对，求梯度呢？

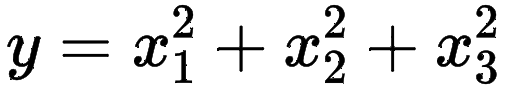
· 其实套路还是一样的，先求偏导，再合成就是梯度，然后取个负就是下降的最快的方向。

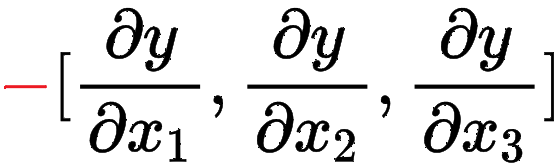
· 无论几维都是一样的！这就是我们大名鼎鼎的梯度下降法（Gradient Descent）。

· 我们把线性回归的梯度下降公式准确写出来应该是这样的

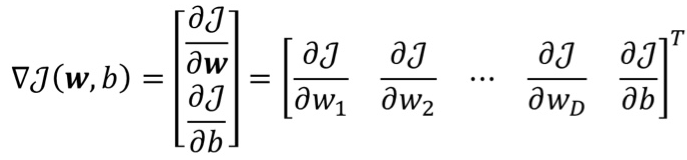
· 这里我们考虑了多个w的情况，即多个影响因素，并且写成了转置之后的形式。

· 有了梯度下降之后就可以进行优化啦，优化公式如下，其实就是不断减。其中α是学习率（Learning Rate），这是一个超参数（Hyperparameter），用于控制优化的速度。

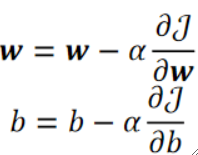
· 学习率是我们遇到的第一个超参数，超参数指的是需要人为进行调整的参数，而不是能学习出来的。

· OK！现在你已经明白梯度下降法了，值得一提的是，即便机器学习、深度学习发展了这么久，就连最前沿的ChatGPT所使用的优化算法，都是梯度下降法，本质是没变的，只是中间的实现过程发生了变化！

两个空间

· 在机器学习中，常用的空间有两个，分别是特征空间（Featured Space）和参数空间（Parameter Space）。

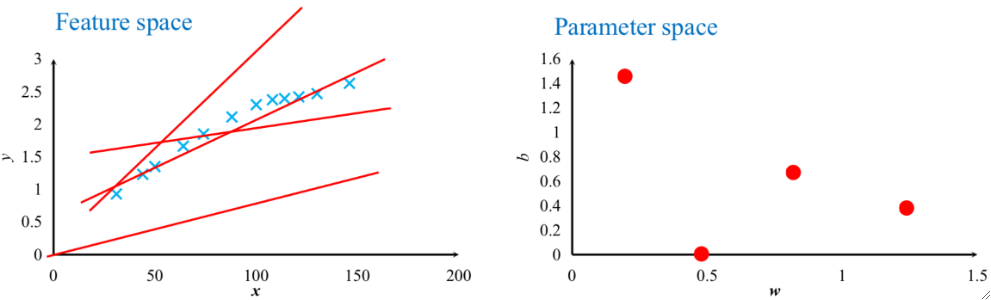
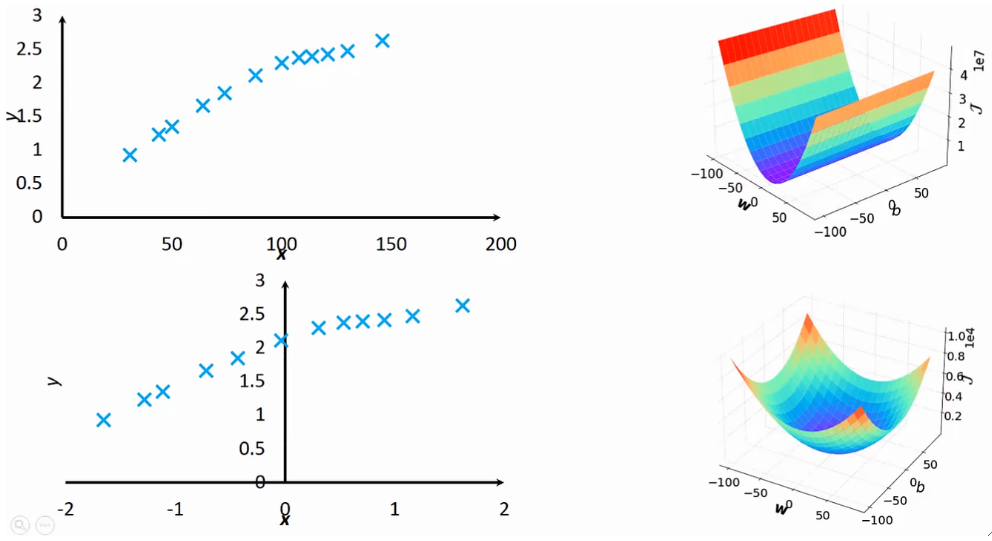
· 特征空间就是我们平常画的x-y图，房价例子的特征空间如下。值得注意的是，在这个函数中，x和y其实都是已知的，就是我们标在图上面的点，反而w和b是未知的。

· 参数空间其实就是把w-b图画出来，也就是说，特征空间上的每一条线，在参数空间上就是一个点。

· 然后，我们给参数空间再加一个轴J，根据代价函数的公式，我们就能把w-b-J图画出来，它长这样

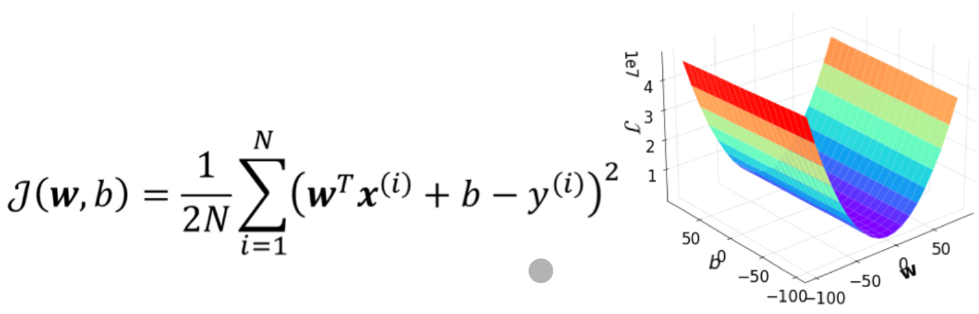
· 有了这个图，哪一个模型是最好的就一目了然了，肯定是J最小的那一个，也就是最下面那一个。

· 然后在此处使用梯度下降，就是求下面这个梯度，然后再取反方向就是下降的最快的方向咯～

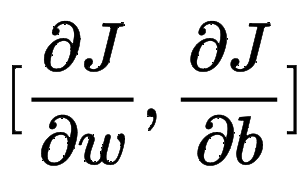
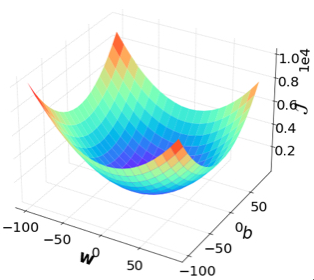
· 补充，其实上面的w-b-J图画出来应该是下面这样的，但为什么在房价的例子中画出来的形状不一样呢？因为在这组12个数据中，w对J造成的影响比b远大的多，这就造成了看上去b对J没什么影响，实际上是有的，只不过很小很小。我们把这种问题称为尺度问题。

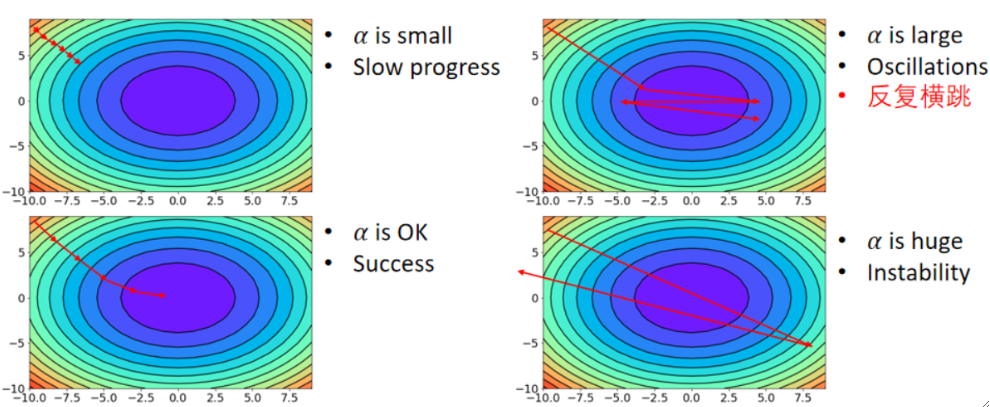
· 在学会了参数空间之后，我们回过头来看看学习率到底有什么作用。下面四个参数空间图我们可以很直观地看到学习率从小到大变化的结果。

① 学习率比较小的时候，学习的过程就很慢。

② 学习率适中的时候，学习的效率就很好。（√）

③ 学习率比较大的时候，就会在最优结果之间“反复横跳”，无法达到最优值。

④ 学习率很大的时候，整个模型就非常不稳定了，基本处于不可用状态。

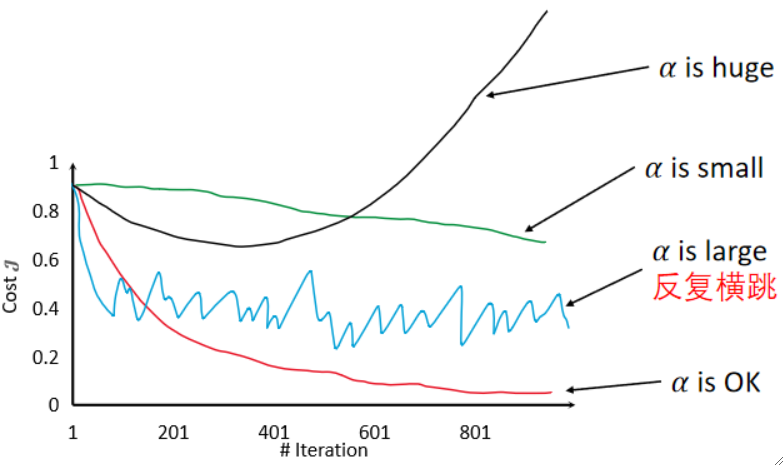
换成曲线图来看会更直观：

归一化（Normalize）

· 我们前面提到了，房价例子中的w和b对尺度不一样，w对L的影响远远大于b，这是很不好的，因为这样很难调整超参数，因此，我们需要找到一个方法，来让w和b的尺度相等。

· 我们使用名为归一化的办法，首先，先求所有样本的均值和方差：

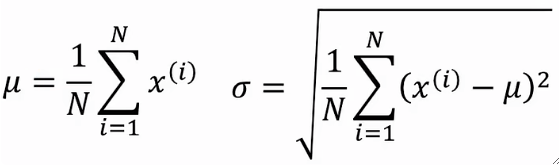
· 然后，我们对所有样本进行如下操作，即自身减去均值再除方差。

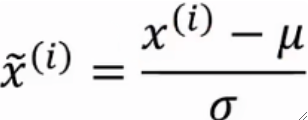
· 然后，我们使用处理过的数据再进行学习，效果会好很多。

· 其中，减去均值的作用是把所有的数据分散到0的左右两边，除方差的作用是把数据聚集在-1到1附近，整体跨度缩小。这样，所有样本的尺度都和b相同了。

梯度下降中的数学计算

· 在了解完梯度下降的原理之后，就来到了计算环节。

· 我们需要计算的是下面两个式子中的偏导数

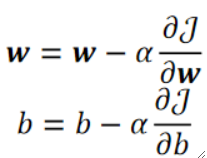
· 首先w中的偏导数，使用链式法则计算过程如下：

（√）

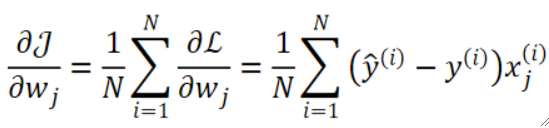其中的偏L偏wj计算过程如下

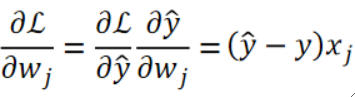
· 同理，b中的偏导数计算过程如下：

（√）

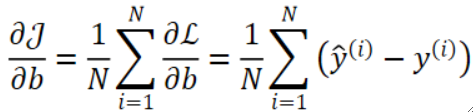
其中偏L偏b的计算过程如下

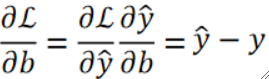
梯度下降存在的问题

· 考虑如下情况

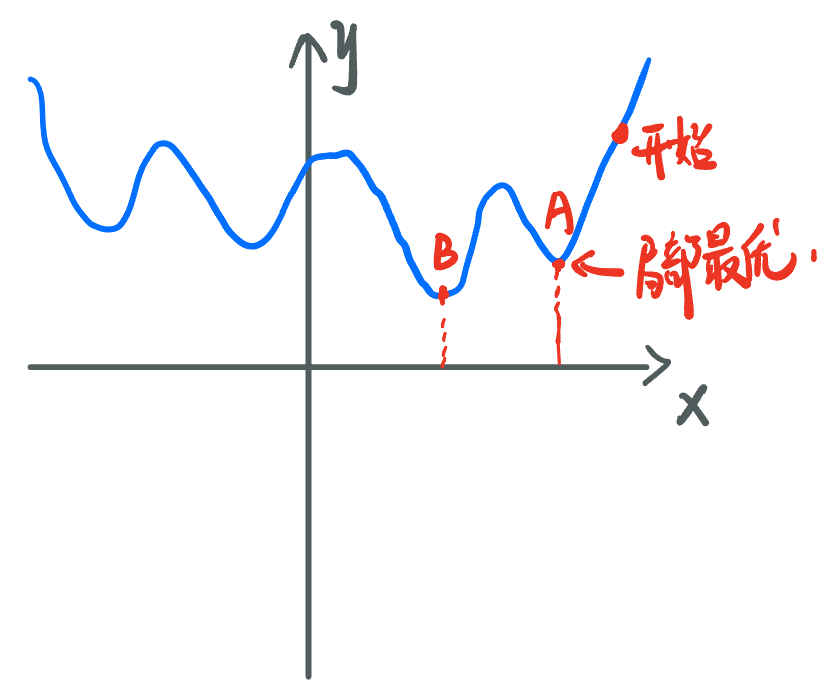
· 可以看到从开始点一直下降回去到A点，但是，A点出y对x求偏导的值就是0，因此会一直卡在A点出不来，但我们知道最低点是在B点处的，因此我们陷入了局部最优（Local Minimal）。

· 再考虑这种情况：

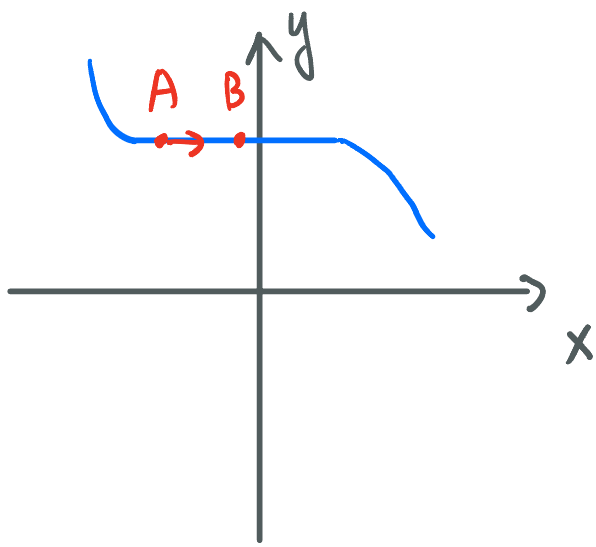
· 如果希望从A点往B点走，很明显做不到，因为此处的斜率无限接近于0，走的速度非常慢。

· 因此，梯度下降算法没有办法保证一定能找到全剧最优！