什么是数据模型?
· 上一章内我们知道,数据库系统可以通过三级模式和两层映射来保证数据独立性,这是上层的东西。
· 那么,在底层,数据应该如何存储呢?这就引出了数据模型的概念,不同的数据模型存储数据的格式不同。
三大经典数据模型
· 目前我们有三种最常用的数据模型,分别是关系模型(表)、层次模型(树)、网状模型(图)。
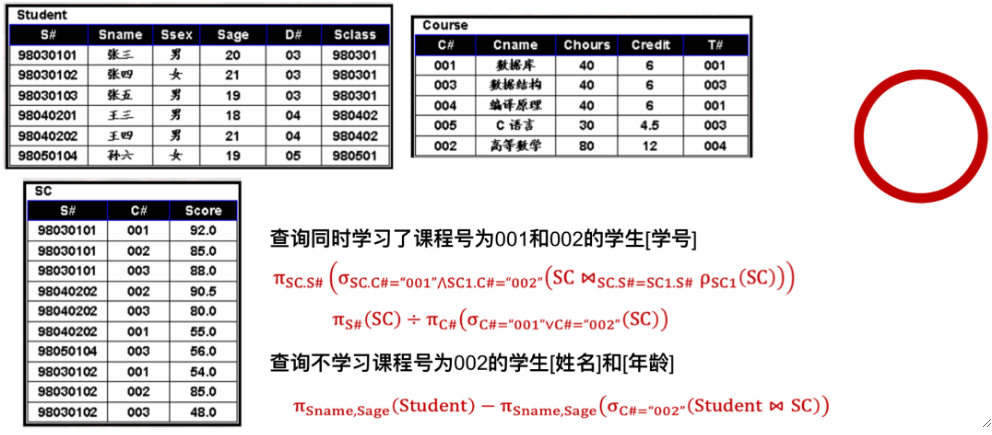
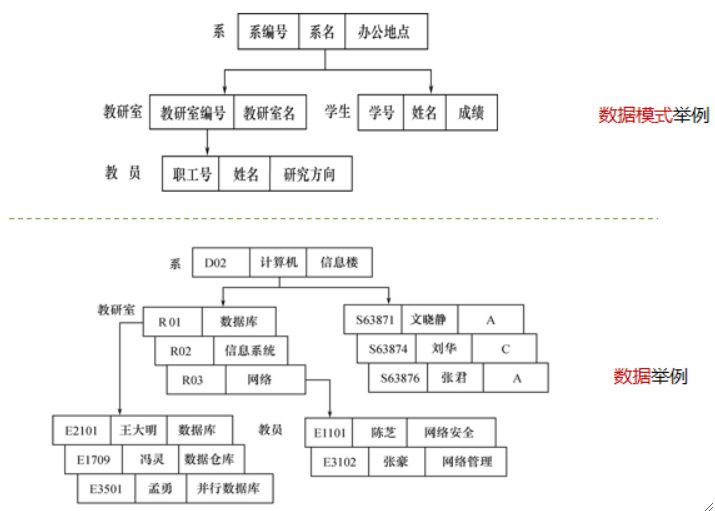
· 以下是层次模型的例子
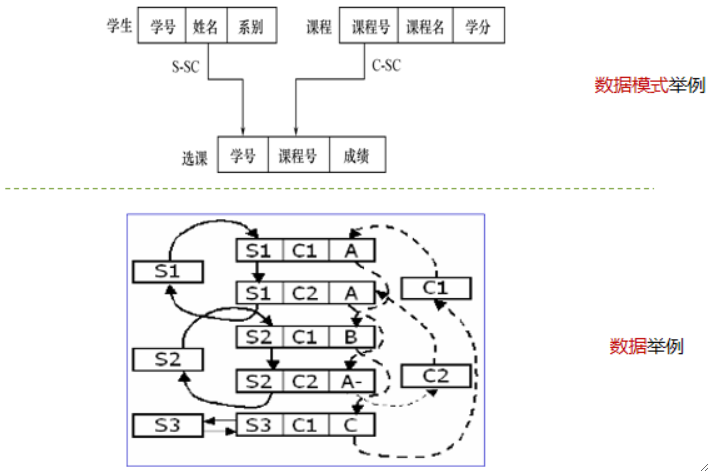
· 以下是网状模型的例子
· 以下是关系模型的例子
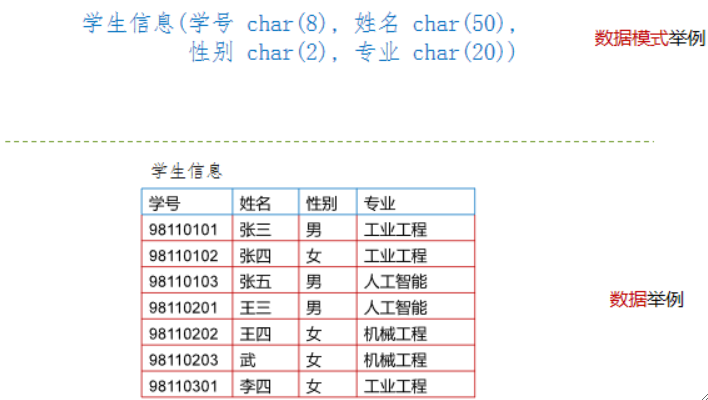
· 而市面上绝大多数的数据库系统,都是采用关系模型去存储数据的。
关系数据模型
关系数据库
· 关系数据库系统是目前使用最广泛的数据库系统。
· 关系数据库与非关系数据库的区别在于,关系数据库只有“表”这一种数据结构,而非关系数据库还有其他数据结构以及相应的操作。
关系模型的基本相关要素
· 一个关系(Relation)就是一张表(Table),一个数据库中有多张有关联关系的表。
· 关系模型的三个要素:
① 描述数据库各种数据的基本结构形式,说人话就是数据库内存在多张表。
② 描述这些结构形式所应遵循的约束条件,说人话就是表头的约束(完整性约束)。
③ 描述表与表之间所可能发生的各种操作(关系操作、关系代数、关系运算)。
关系模型的数据结构
① 属性和域
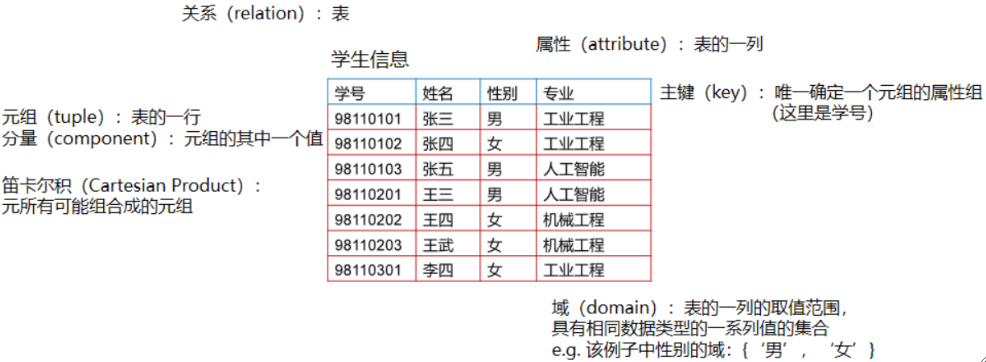
· 域(Domain),一组具有相同数据类型的值的集合,说人话就是表的一列的取值范围。
· 属性(Attribute),不同列可以对应相同的域,为了加以区分,每个列都要起个名字,称为属性,说人话就是表的某一列。
· 下面例子中,有4各属性(4列),“性别“的域为{'男', '女'}。
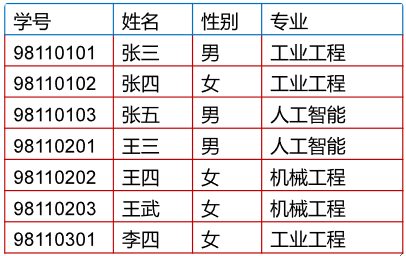
② 元组和分量
· 元组(Tuple),和属性一一对应的具体取值的集合,说人话就是表的某一行。
· 分量(Component),元组中的其中一个属性的取值,说人话就是元组中的某一个值。
· 下面的例子中,”李四“所在的行就是一个元组,她的性别就是一个分量。
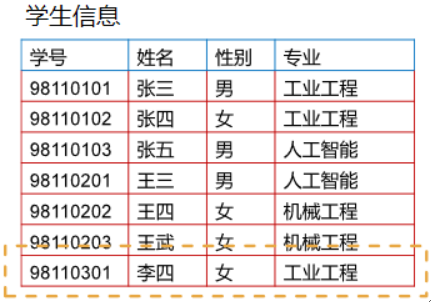
③ 笛卡尔积
· 笛卡尔积(Cartesian Product),所有可能组合成的元组的集合。
· 基数(Cardinal Number),笛卡尔积的数量。
· 直接看例子,已知三个域如下,求这三个域的笛卡尔积(D1×D2×D3)。
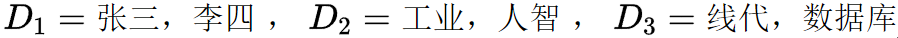
· 所有可能的组合数(基数)为2*2*2=8,结果如下
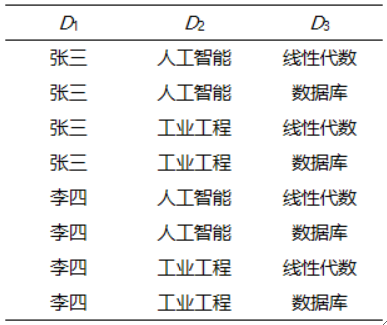
· 注意,笛卡尔积不一定有意义,比如上面的例子,张三不可能又是人工智能专业,又是工业工程专业的。
④ 关系
· 关系(Relation),有很多个域D1,D2,......,Dn,它们的笛卡尔积(D1×D2×......×Dn)的子集称为在域D1,D2,......,Dn上的关系,表示为R(D1,D2,......,Dn),其中R是关系名。
· n表示关系的目或度(Degree),n目关系必有n个属性,R(A1,A2,......,An)。
· 不要被上面那句抽象的定义误导了,关系实质上就是一张表,一直没变过!
⑤ 码(键)
· 码(键,Key),用于标识每一行或与另一个表产生联系。
· 候选码(Candidate Key),能唯一地标识一个元组的最小属性组,是主码的候选。如下表中,(学号),(姓名)都是候选码,虽然(学号,姓名)也能唯一标识一个元组,但不是最小的,所以不是候选码。
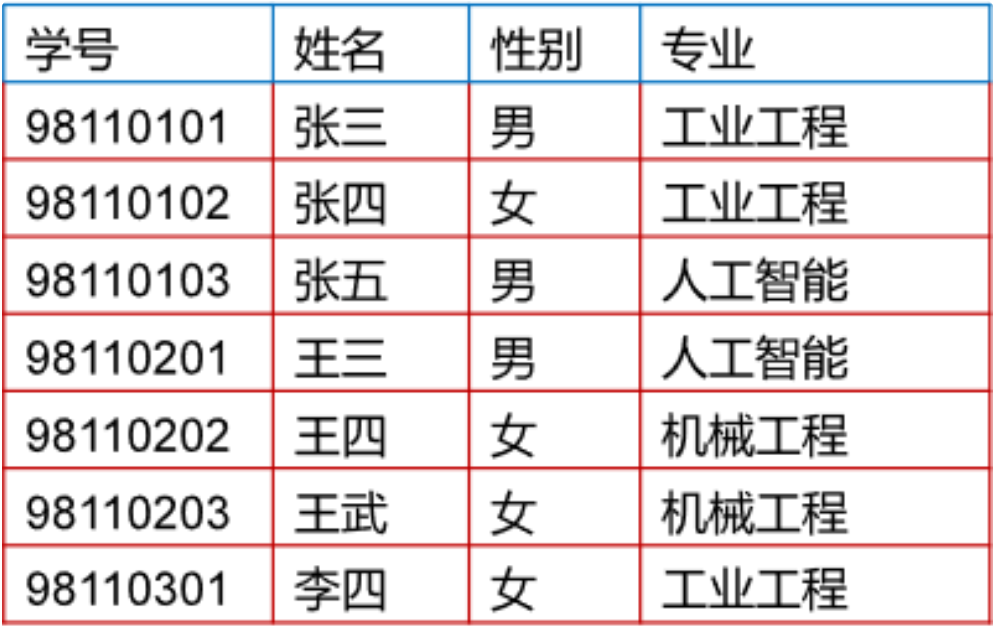
· 全码(All Key),关系模式的所有属性组成了候选码,如某个关系模式R(T,C,S)其中T代表教师,C代表课程,S代表学生,若一个教师能开多个课程,那就只有三个属性都用上才能唯一标识一个元组了。
· 主码(Primary Key),其中一个候选码,一般人为指定。
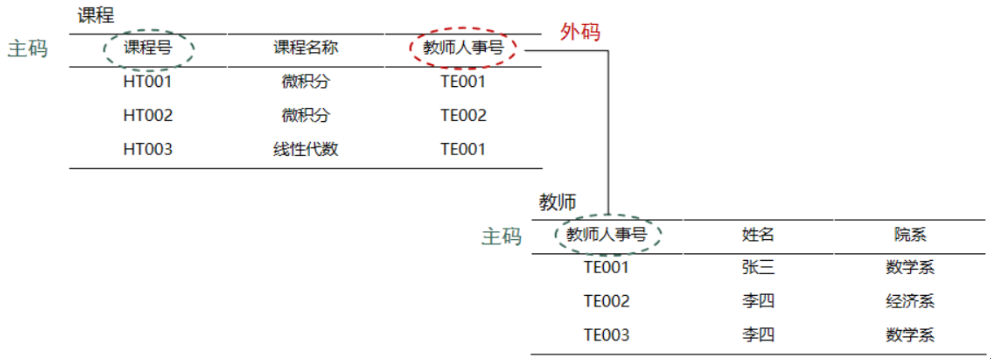
· 外码(Foreign Key),不是候选码,但是和另一个关系(表)中的候选码对应,用于连接两个关系。以下是一个外码的例子,在课程表中,主码是课程号,教师人事号不是候选码,可以作为外码,它与教师表中的主码,即人事号对应,这样,课程表和教师表就连接起来了。
⑥ 总结关系模型的数据结构
基本关系的性质
① 关系中的列
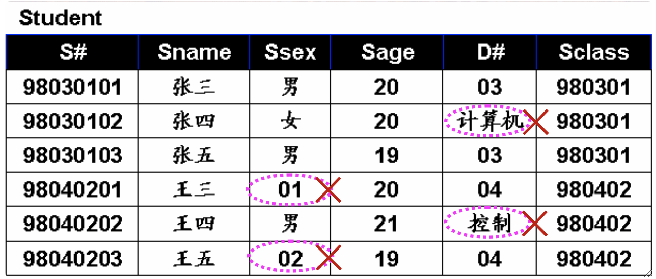
· 列的同质性,即每一列的分量来自同一域,是同一类型的数据。
· 下面的例子中,Ssex很明显是性别,只有域中只有男女,出现01、02就是非法的值。
· 不同的列可以来自于同一个域,但是一个关系中不能有重复的属性(不能有完全一样的两列)。
· 列的顺序无所谓,可以随意更换。
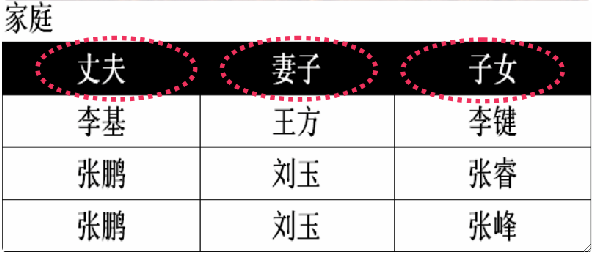
② 关系中的行
· 关系中的两个元组不能完全相同(不能有两条完全一样的记录)。
· 行的顺序无所谓,可以随意更换。
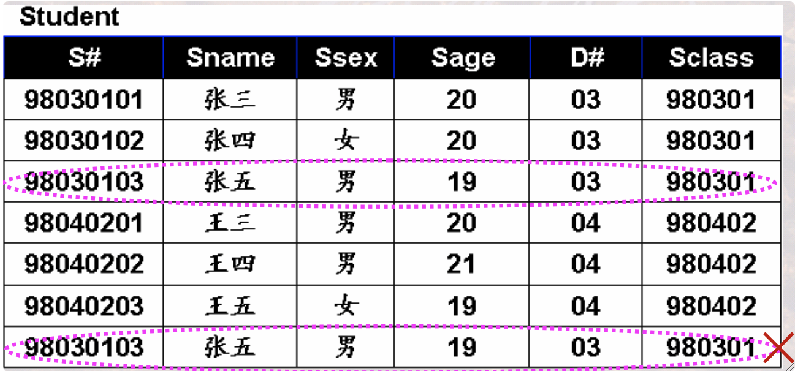
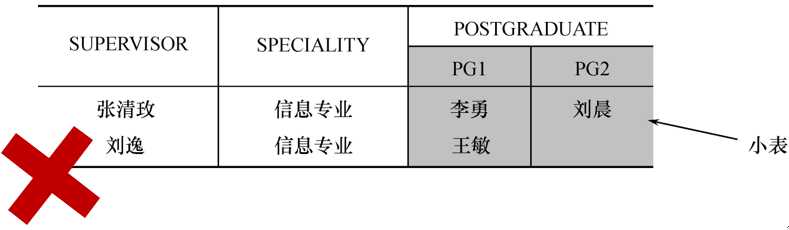
③ 关系的第一范式
· 属性不可再分!即不能有“小表”。
关系的完整性
关系的三类完整性约束
· 实体完整性、参照完整性、用户自定义完整性。
· 关系模型必须满足前两个完整性,称为关系的两个不变性,应该由关系系统自动支持。
实体完整性(对主码的限制)
· 关系的主码的属性值不能为空值!
· 一个元组代表一个实体,主码是用于唯一标识该实体的,如果主码为空值(即不明确或无意义的值),就说明这个实体无法被标识、区分,这肯定是不允许的!
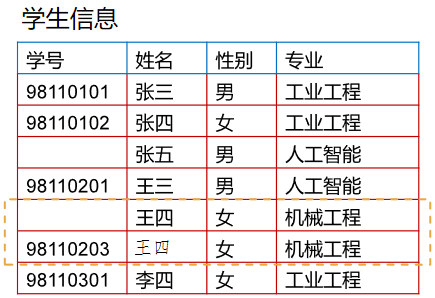
· 上述例子中,很明显主码是学号,但是张五和王四缺失了主码(学号),这肯定是不允许的。
· 空值(Empty Value),在进行关系操作的时候,有时关系中的某些属性值暂时无法填上,如“生日不详”,“年龄不详”等,这个时候就要用空值来代表这个情况,在关系模型中用“?”或“NaN”来标识。
· 有了空值就会对我们的关系运算造成很大影响,如“3 + ?”是无法计算的,因此对空值需要进行特殊处理。
参照完整性(对外码的限制)
· 如果关系R1的外码Fk与关系R2的主码Pk相对应,则R1中的每一个元组的Fk值或者等于R2 中某个元组的Pk值,或者为空值。
· 说人话:外码如果是别人的主码,那外码的值要么是别人主码的域里面的值,要么为空,但不能凭空多出来值!
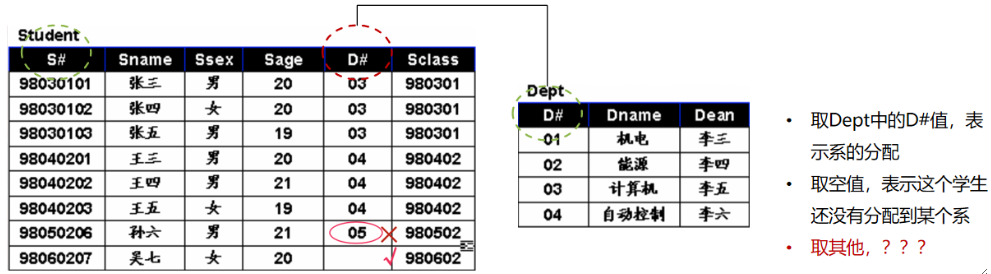
· 如上述例子中,Student的D#取了一个05是错的,因为Dept表中的D#没有05,但是取空值是可行的,代表还没分配。
用户自定义完整性(对属性和属性组的限制)
· 用户针对具体的应用环境定义的完整性约束条件。
· 关系模型应该提供定义和检验这类完整性的功能,如定义属性“学号”为10位整型数字,关系模型应该在写入数据的时候检测数据是否满足要求。
关系代数
常用的关系操作
· 查询(Query):选择、投影、连接、除、并、交、差
· 更新(Update):插入、删除、修改
· 5种基本操作:并、差、笛卡尔积、选择、投影
关系操作的特点
· 集合操作方式,即操作的输入和输出都是集合,一次一集合的方式。
关系代数的运算
· 用关系代数,表示关系运算,指明操作,具有过程,指导其他数据库语言的撰写。
集合运算
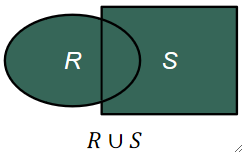
① 并(Union)
· 首先,有两个关系R和S,它们有相同的目(即属性个数相同),属性都来自同一个域。
· 用R∪S来表示并运算,运算结果仍是n目关系,图示如下。
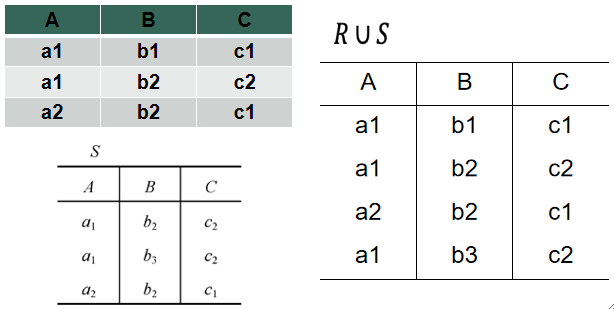
· 例子如下
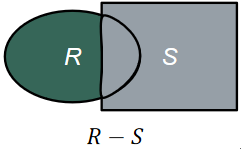
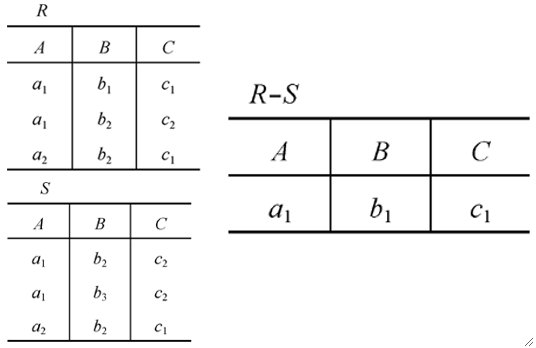
② 差(Difference)
· 首先,有两个关系R和S,它们有相同的目(即属性个数相同),属性都来自同一个域。
· 用R-S表示差运算,注意,R-S和S-R表示的结果不一样!不是同一个关系!图示如下
· 例子如下
③ 笛卡尔积(广义版)
· 首先,有两个关系R(n目,k1个元组),S(m目,k2个元组)
· 用R×S表示笛卡尔积运算,最终会有k1*k2个元组,例子如下

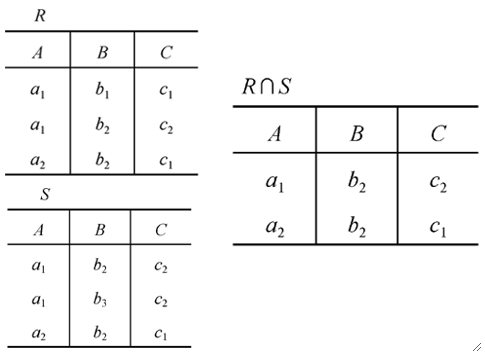
④ 交(Intersection)
· 首先,有两个关系R和S,它们有相同的目n,相应的属性都取自同一个域。
· 用R∩S表示交运算,结果仍为n目关系,由既属于R也属于S的元素组成。
· 例子
关系运算
① 一些必要符号的定义
· 后续的运算会用到以下的符号,此处先给出定义。
② 选择(Selection)
· 选择又被称为限制(Restriction)。
· 首先,有一个关系R,有一个条件F,定义选择运算符为σ。
· 用 \sigma_F(R)表示选择运算,指的是从关系R中选择出满足条件F的记录。
· 条件F是一个逻辑表达式,它的结果是个布尔变量。
· 比较表达式指的是形如 xθy 的表达式,其中θ是二元比较符。可以用与(⋀ )、或(⋁)、非(¬)来连接多个表达式。
· 计算优先级:括号->比较->非->与->或
· 举个例子,有如下学生表
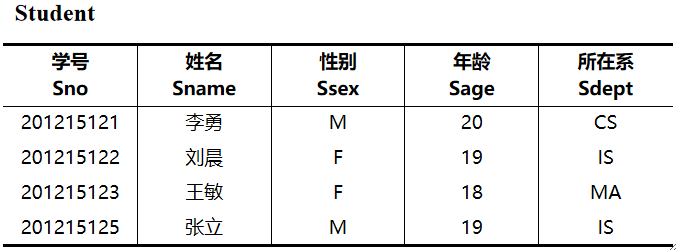
· 选出所有IS系的学生:
· 选出18岁以上(不含)的学生:
· 选出18岁以上(不含)的男生:
· 习题


③ 投影(Projection)
· 首先,有一个关系R(A1....An),有一个属性组A,定义投影运算符为π。
· 用\pi_{A}(R)表示投影运算,指的是从关系R中选出属性组A组成新的关系。
· 投影之后不仅取消了原关系中的某些列,而且还可能取消某些元组(避免重复行)。
· 例子,有如下学生表
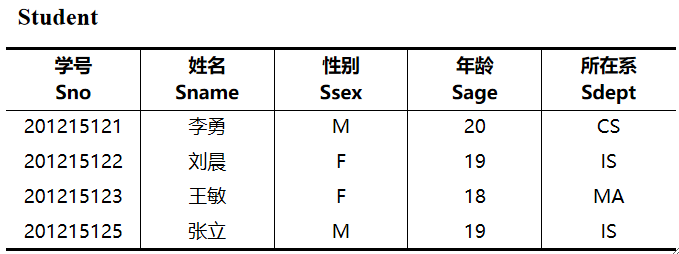
· 求\pi_{Sdept}(Student)的结果?
· 习题

④ 连接(Join)
· 首先,有关系R(A1......An)和S(B1......Bm),属性组A、B,定义连接运算符为⋈。
· 用R\bowtie_{A \theta B}S表示连接运算,指的是从R、S的笛卡尔积中选取满足AθB关系的结果。
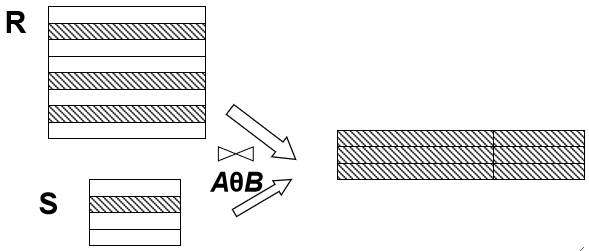
· 例子,有R、S两个表
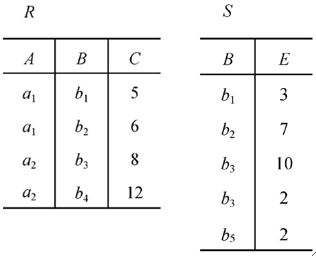
· 写出满足R\bowtie_{C<E}S的结果
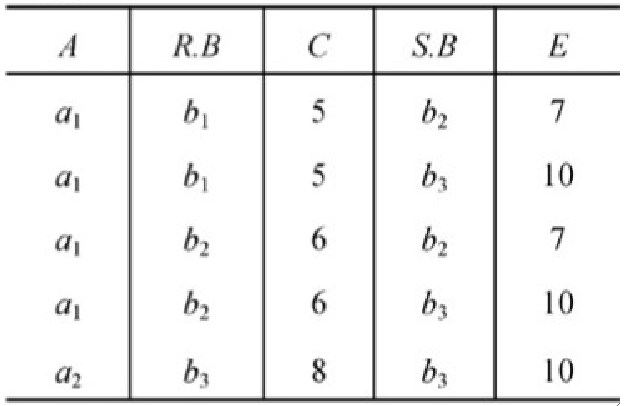
· 再来一个具体例子
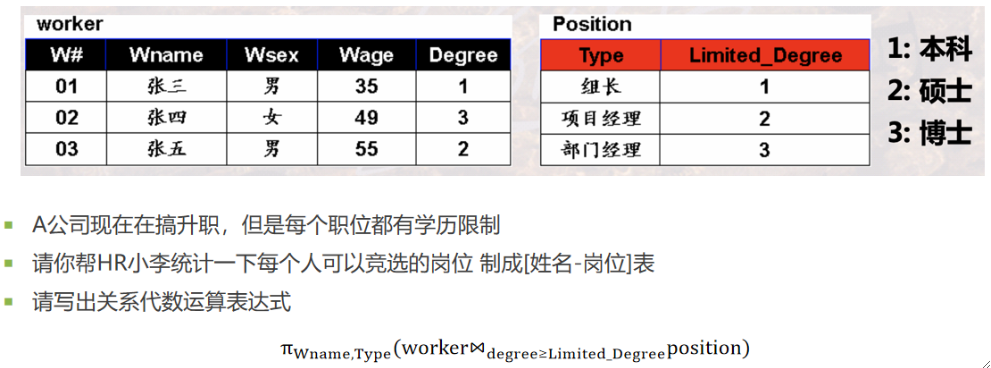
· 两类常用的连接:等值连接和自然连接。
· 等值连接(Equal Join),θ为“=”,选取A,B中相同的值。
· 自然连接(Natural Join),是一种特殊的等值连接,两个关系中进行比较的分量必须是相同的属性组,在结果中把重复的属性列去掉。
· 例子,有如下两个关系
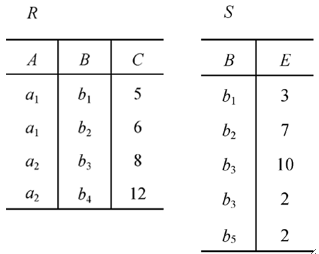
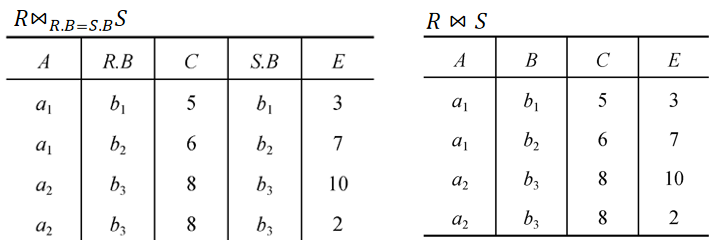
· 求R和S的等值连接R\bowtie_{R.B=S.B}S和自然连接R\bowtie S。
· 再来一个具体例子
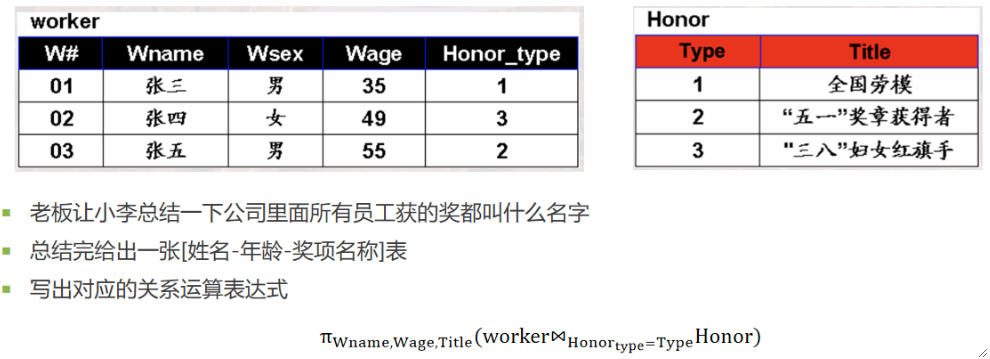
· 还有一种比较特殊的连接,自己和自己连接。
· 首先,有一个关系R,然后使用“改名卡ρ”把关系R更名为关系R1:
· 然后自己和自己连接,进行表内查询,如下例子先自己和自己连接,然后查询S#为101和202的记录。
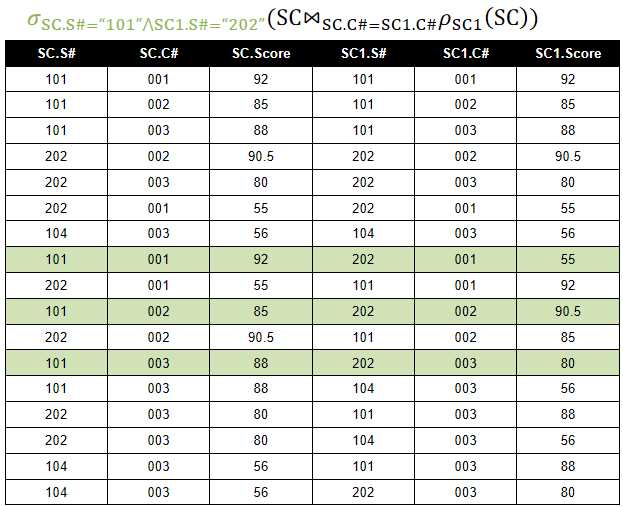
· 接下来要先介绍一个概念,悬浮元组。
· 悬浮元组(Dangling Tuple),在两个关系R、S进行自然连接的时候,关系R中某些元组有可能在S中不存在公共属性上值相等的元组,从而造成R(或关系S)中这些元组在操作时被舍弃了,这些被舍弃的元组称为悬浮元组。
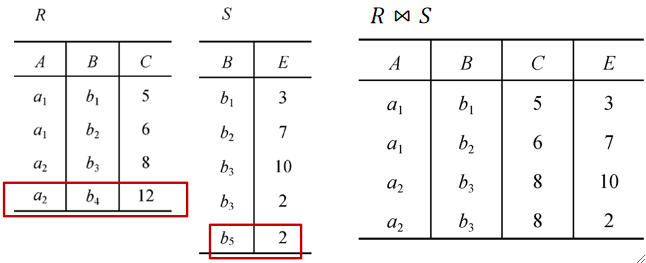
· 举个栗子,下面的R、S进行自然连接时,R(a2,b4,12)和S(b5,2)被舍弃了,因为没有找到公共属性B上值相等的元组,所以这两个就是悬浮元组。
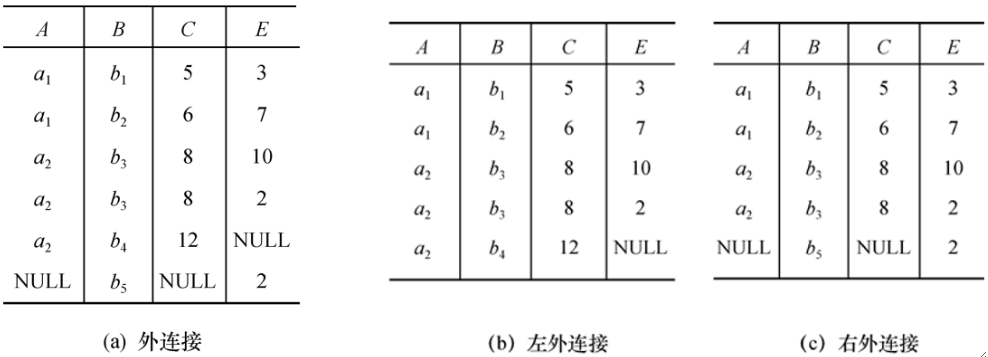
· 接下来介绍另一种特殊的连接,外连接。
· 外连接(Outer Join),也称全外连接,即在进行自然连接的时候,把本应舍弃的悬浮元组也保留在结果中,在其他属性上填上空值(NULL)。
· 左外连接(Left Outer Join或Left Join),只把左边关系R中要舍弃的元组保留就叫做左外连接。
· 右外连接(Right Outer Join或Right Join),只把右边关系S中要舍弃的元组保留就叫做右外连接。
· 在上述例子中,我们找到了R和S的两个悬浮元组,那么就可以写出外连接、左外连接、右外连接如下:
· 一些实际例子
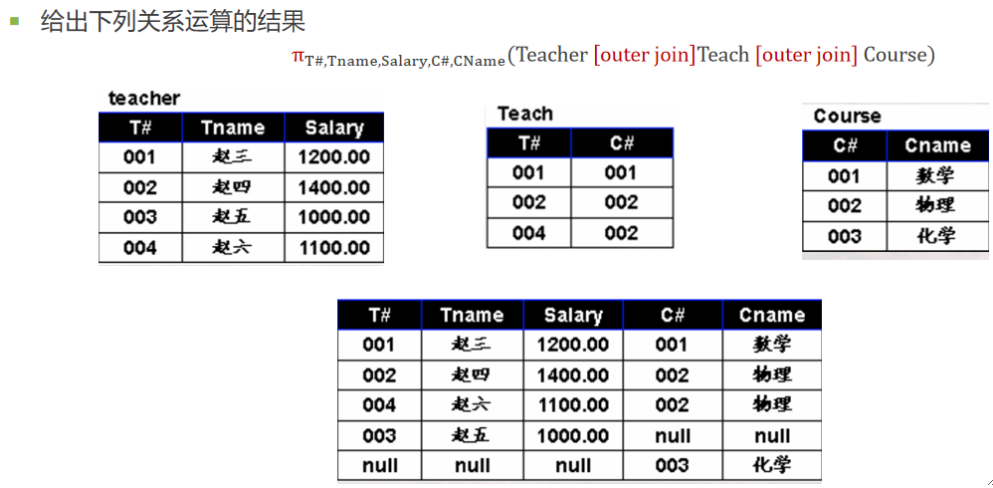
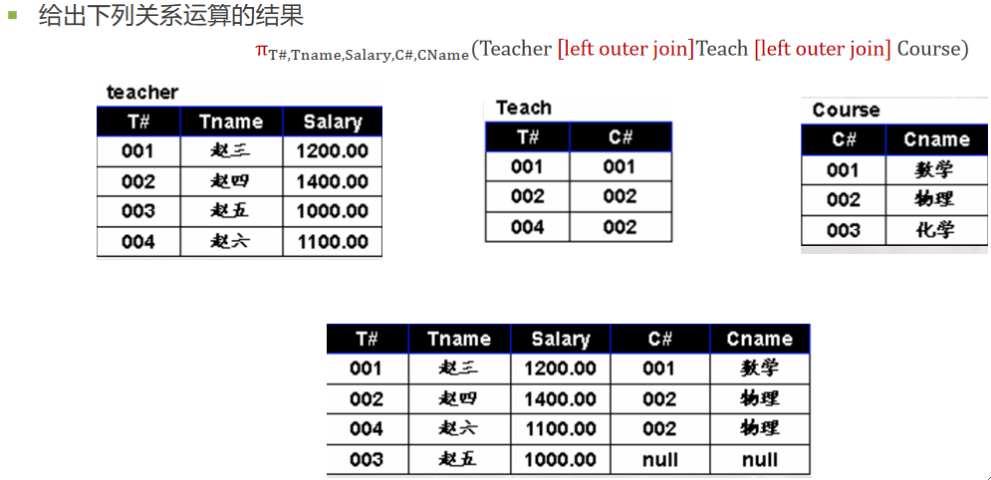
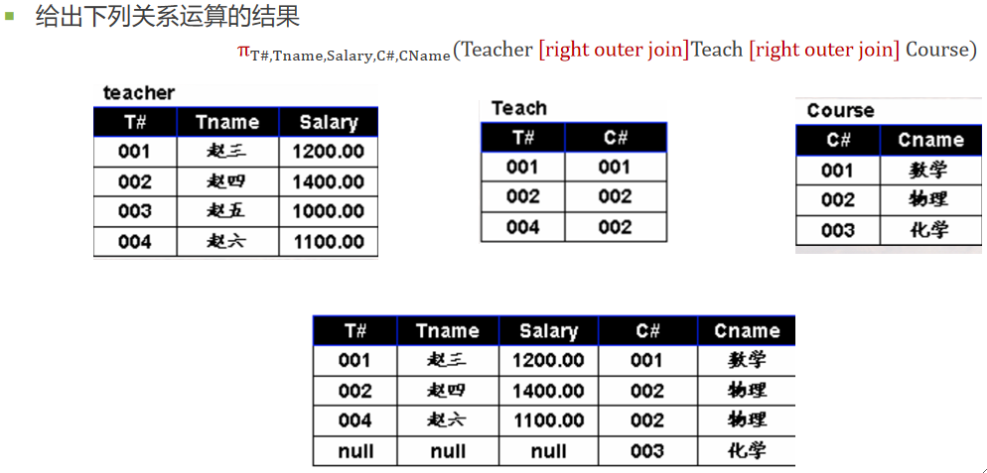
⑤ 除(Division)
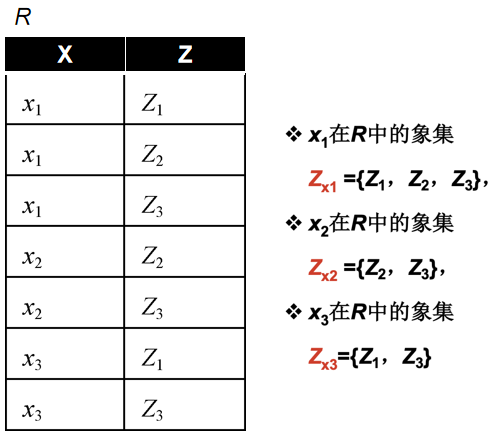
· 首先,先介绍一个新概念,象集。
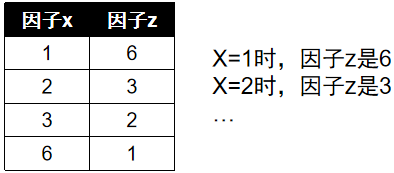
· 象集(Image Set),把表想象成一个结果相同的乘法表,象集就像是在找某个值的因子,我们直接看例子。
· 在下面的乘法中,有两个因子x、z,相乘的结果都是6,当X=1的时候,找到因子Z=6。
· 把这个概念应用到象集里面去,有如下表,找x1在R中的象集就是Z1、Z2、Z3。
· 接下来介绍除运算。
· 首先,有关系R(X,Y)和S(Y,Z),其中X、Y、Z是属性组。R的Y和S的Y可以有不同的属性名,但必须出自同一个域集。
· 定义R÷S为除运算,得到一个新的关系P(X)。除法的整个定义很抽象,我们直接看例子。
· 求R÷S
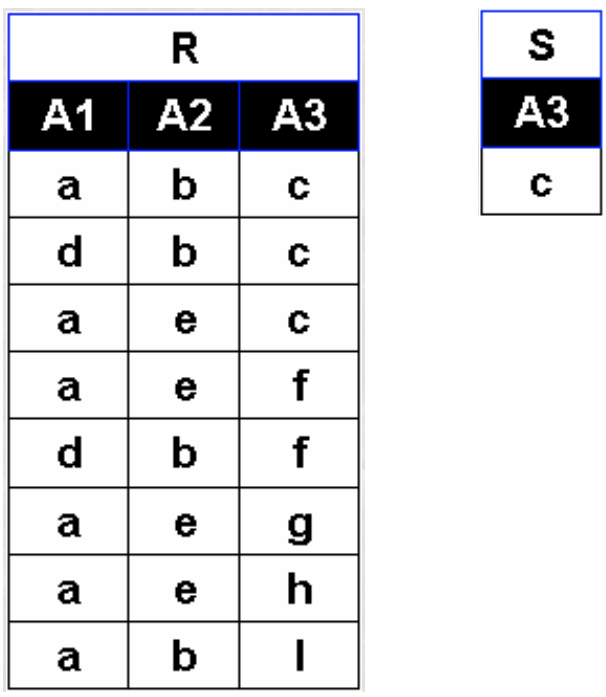
· 首先找到R中所有的c
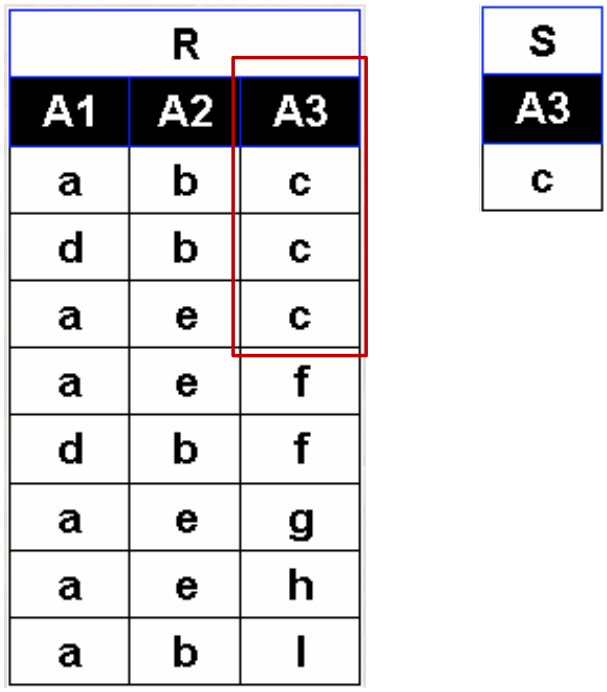
· 然后求象集
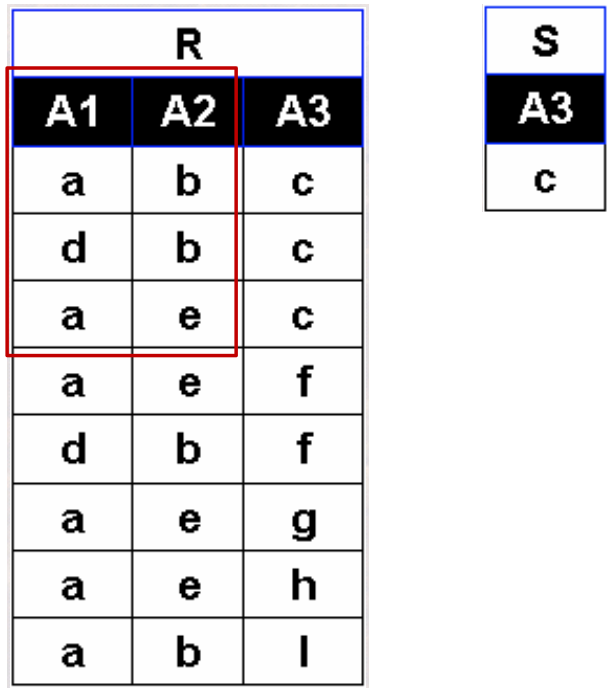
· (a,b),(d,b),(a,e)都满足条件,故新关系为
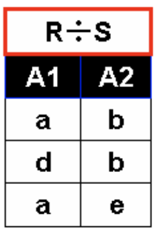
· 再来一个例子,求R÷S
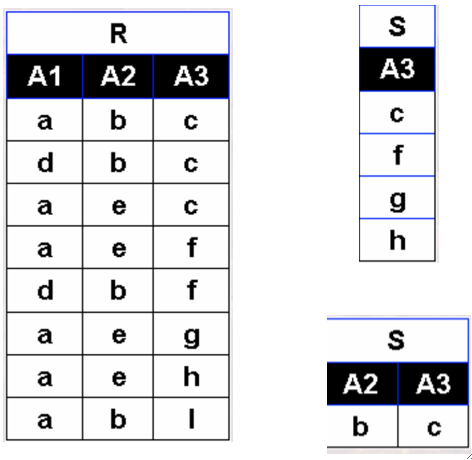
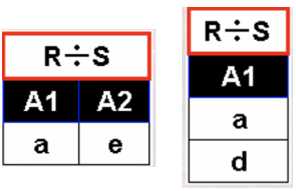
· 直接给答案
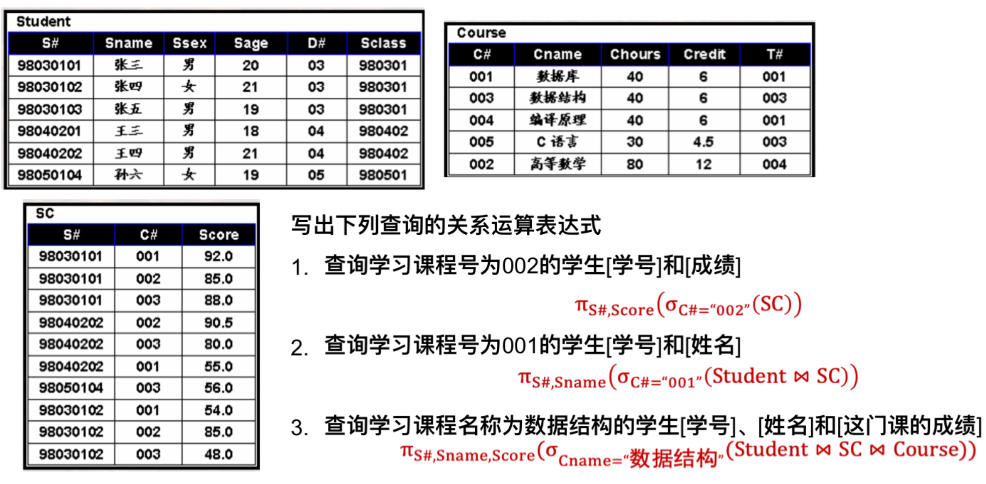
课后习题
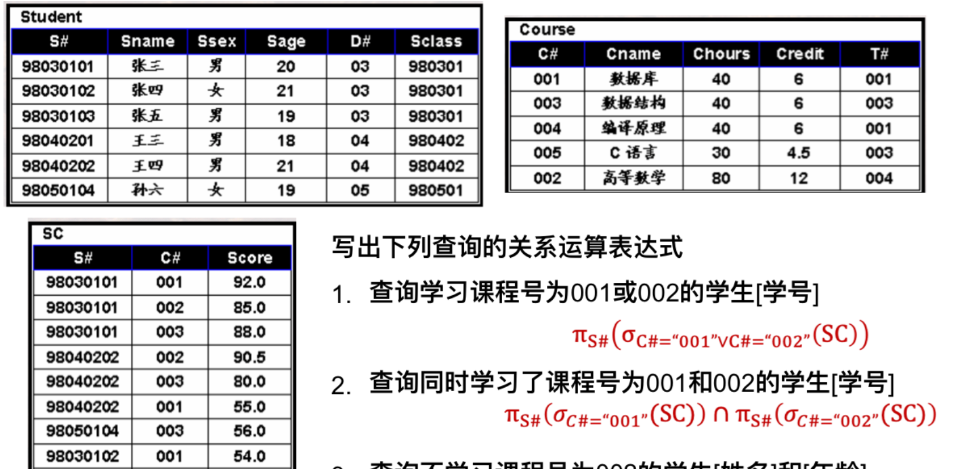
· 注意,以下写法是错误的
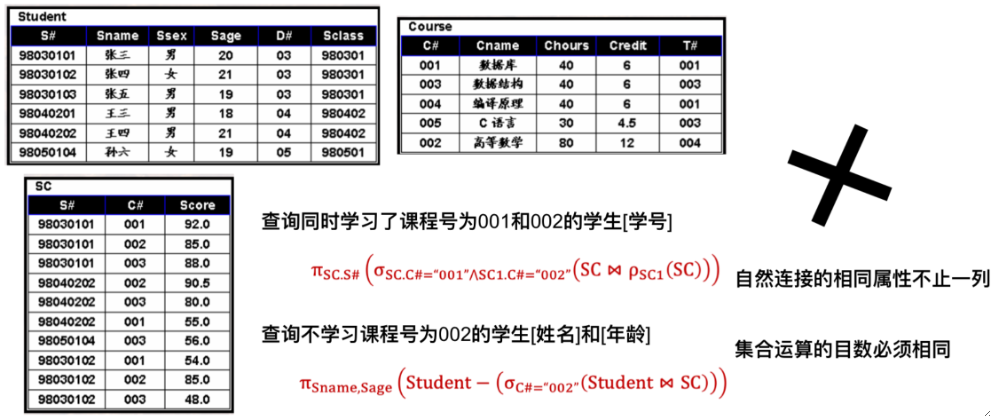
· 下面的写法是正确的