卷积神经网络
· 卷积神经网络(Convolutional Neural Networks,CNN)就是为了处理图片而生的。
· 一般来说,我们会使用CNN对图片进行多分类,如经典的猫狗分类。
样本
· 首先,我们的样本是一张一张的图片,假设一张图片的宽为W高为H,那么其实一张图片就包含了W*H个特征x。
· 然后,我们把每一行的每一个像素“拉直”,相当于把W*H的矩阵变成了一个(W*H)*1的矩阵。如下图,就有D=(W*H)*1个特征。然后给每个特征打标签,如我们用0代表猫,1代表狗。
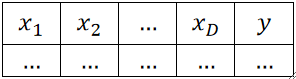
· 这样,有N张图片,就有N个样本,N个像上面一行一行的特征。与前面不同的是,现在每一行的特征会非常非常大,如人脸识别倾向于使用112*112大小的图片,那也就是一张图片包含了10000+的特征,这是很恐怖的,这就是深度学习。
· 当然,我们打完的标签还是要转换为独热向量(One-hot Vector)的!
· 当然,一张图片除了宽高之外,还有一个我们需要考虑的东西,就是通道(Channel),如最常见的RGB通道。那其实本质上一张图片我们就要处理三个矩阵而不是一个矩阵了,这样子特征数量直接翻了三倍!即W=D*H*3。

传统神经网络?
· 如果我们要使用传统的全连接神经网络,假设一张800*800的图片,那就有64万个特征,那在一层神经元内,就要计算64W*第一层神经元个数次,这是非常恐怖的计算量。
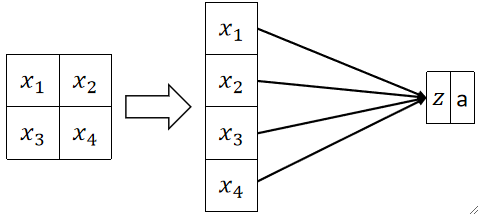
· 我们也可以用卷积的角度来理解全连接层,现在你不知道什么是卷积也没关系,我们只需要拿一个和图片大小一模一样的矩阵与其点乘后求和,就是全连接层的输出结果。
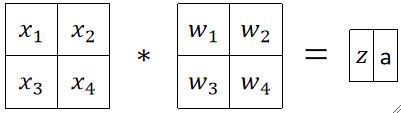
· 可以注意到,用原来神经元的计算得到的式子是z=w_1x_1+w_2x_2+w_3x_3+w_4x_4,而使用卷积的角度计算的时候我们故意把四个x换了一下位置,那么得出的结果就是z=w_1x_3+w_2x_4+w_3x_1+w_4x_2+b,其实这本质上是一样的,因为只有人类有位置的概念,在计算机看来没有位置的概念。如果原来神经元的四个w分别是1、2、3、4,那在卷积角度的w是3、4、1、2,本质上是一样的。
卷积层
· 我们知道,直接使用神经网络的全连接层进行图像的识别任务是几乎不可能的,因为计算时间和内存成本都太大了。
· 卷积的好处就在于大大减少了计算量,如下图,我定义的卷积核的大小是2*2,则计算一个z就只与被卷积核乘过的4个x有关,而不是像全连接层那样与16个x都有关。准确来说,原来要计算16个w*x,然后再做16个左右的加法把他们加起来,那就是总共要做32次左右的计算,现在只需要做4次乘法和4次左右的加法,总共只用做8次左右的运算,那运算量直接下降了80%,这是非常可观的!这个例子还只是基于一张16*16的图片,一般来说做人脸识别需要用到100*100的图片,那计算一个z的计算量在3*3的卷积核的情况下就从10000+10000减少到了3*3+3*3,这个优化简直是太可观了!
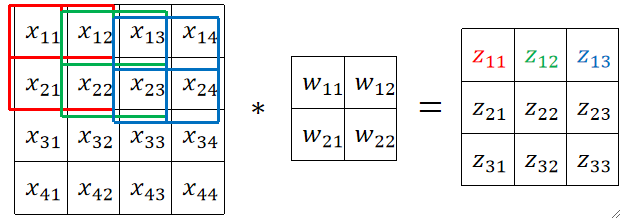
· 接下来我们正式地看看卷积如何计算。
① 首先我们需要先确定输入的图像的大小,此处我们的图像大小是L_{in}=4,即4*4的图像。
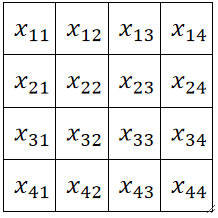
② 首先,我们需要定义一个卷积核,这个卷积核一般就是长宽一致,如下面的图我们就定义卷积核大小为L_{in},即2*2的卷积核。
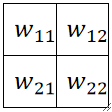
③ 然后,卷积的计算方式就是拿卷积核与原图像一个个相乘,因此我们需要定义一个步长(Stride),即每次滑动多少格,此处我们定义步长为L_k=1。
④ 然后就可以开始计算了,如下图,红->绿->蓝其实就是滑动了2次,做了3次卷积的结果。如果一行走完了,就直接跳到下一行进行计算即可。
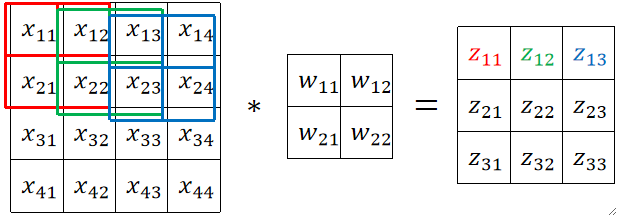
不要忘记z是乘完之后求和的结果,并且还要加上偏置b,而且还需要进入relu激活函数对结果进行激活,最后得到的a才是真正的卷积结果:
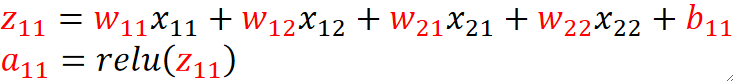
⑤ 可以发现,卷积核总共走了9步,每一行走3步,那么我们就有输出的矩阵大小L_{out}=3,即输出的是3*3的矩阵。
⑥ 总的来说,我们在代码实现的时候,可以先用原矩阵与卷积核进行运算:
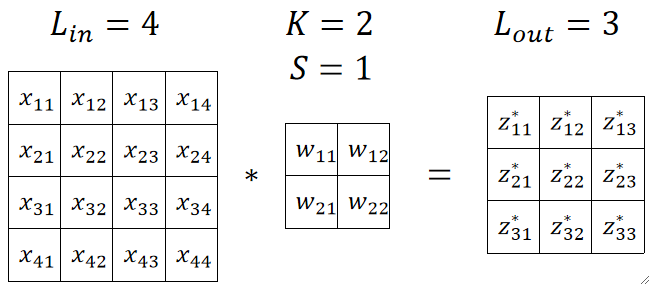
然后初始化一个偏置矩阵,加上去:

最后使用relu对整个矩阵进行激活:
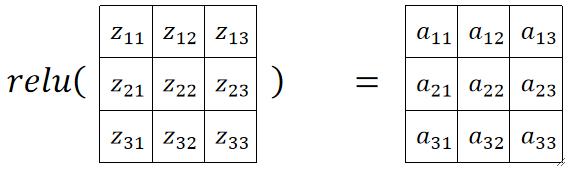
填充 Padding
· 我们发现,原图片经过卷积之后变小了,如果在深度神经网络中,卷积次数不止一次,那最后图片就会越来越小,这不是我们所希望的。
· 因此,我们要使用一个被称为Padding的操作,先对输入的图像进行填充,再进行卷积。
· 在正式讲Padding之前,我们先思考一下,Lout,即卷完后的大小,能否能算出来呢?答案是可以的,公式如下:
· 接下来我们正式讲Padding,还是使用上面的例子,原来输入图片的大小是4*4,然后我们给他在尾部补上一圈:
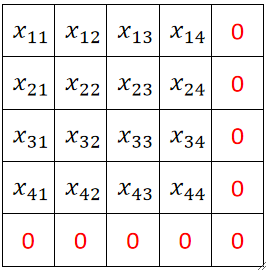
· 这么做的好处就是输出的图像大小不变了,但坏处就是会造成一点精度的损失,但这个损失并不大,所以可以忽略不计。
· 至于填充多少圈才能保持不变,就根据Lout来计算即可。
· 当然,填充的位置可以是头部也可以是尾部,这个问题不大。
· 既然加上了Padding,那么我们在计算Lout的时候也需要作出改变,把P考虑进来即可:
· 注意在进行Padding的时候,如果要进行多于1次都Padding,则需要头尾轮流进行,否则会导致某个x被过度访问,某个x被过少访问的不平均的情况,而且如果Padding次数过多,也会导致最后卷积核和一个全0矩阵相乘,那就完全没有意义了。一般来说就是在外面包一圈0,即P=2。
· 现在我们可以再分析一下卷积操作到底提高了多少效率。
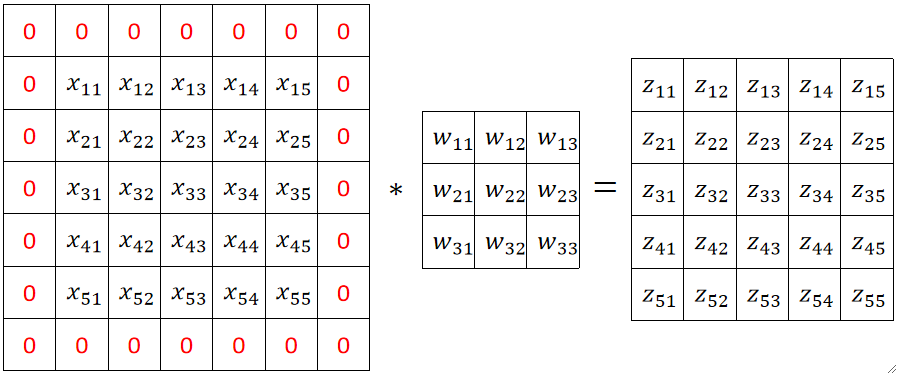
· 假设Lin和Lout都是5,因为有Padding,那在使用传统的全连接神经网络的时候,每一个x对应一个参数,即25个x有25个参数w,一个输出z由25个x和25个w相乘得到,那要25个z就要25*25个x和w相乘得到,也就是说最终的参数量为25*25=625个。
· 然后我们来计算浮点数计算量(FLOPs),这个数反应了模型的计算速度,越小越快。我们刚刚知道总共有625个参数,估算一下,要得到每个结果,要有25个乘法,然后再把它们加一起,大概是25*2,然后25个输出,所以总共有2*25*25=1250,当然我们忽略到了加上偏置b。
· 那我们来分析卷积的话,参数量就是卷积核的大小K*K=9,FLOPs就是2*K*K*Lout*Lout,即2*3*3*5*5=450,这个很明显参数量少了很多且快了很多。
为什么是卷积?
· 现在我们知道了卷积能快速提取图片的特征且能显著的提高效率,那,为什么是卷积操作?为什么不是其它操作?这说明卷积本身就具有一定的意义!
· 首先我们应该要知道的是,卷积核(Convolutional Kernel)这个东西在CNN被发明之前就存在了很久了,在数字图像处理中,卷积核被称为卷积滤波器(Convolutional Filter),为什么叫滤波器,因为它可以帮我们过滤掉我们不需要的信息,只留下我们需要的信息。
· 我们人为设计了许多卷积滤波器,如大名鼎鼎的Prewitt Kernel,它是用来对图像做边缘检测(Edge Detection)的。
· 它包含了两个卷积核,w1用于提取竖直的边缘,w2用于提取水平的边缘,分别提取完之后组合起来就是边缘信息了。

· 从这个例子我们就可以证明,卷积核是具有提取特征作用的。 而CNN,就是帮我们自动学出来一个卷积核,然后通过这个卷积核提取出来的特征,送入神经网络让他进行分类。
· 其实,使用多个卷积核其实就是采用了分而治之的思想,每个卷积核负责提取图像某一部分的特征,然后最后把特征组合起来。
池化 Pooling
· 我们知道,卷积核运算完后会输出一个值,这个值越小就代表特征越少嘛。然后会把卷积完的矩阵送入relu激活函数(max(0,z)),小于0的值都会变成0。
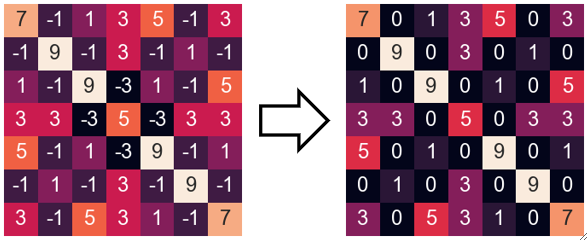
· 可以发现,经过relu之后很多元素都变成0了,这些0往后算已经没有意义了,它们不包含任何信息,因此我们想到,能不能把这些0丢掉一些,以减少后续的计算量呢?答案是肯定的,这就引出了我们的池化操作。
· 池化的过程其实跟卷积很像,首先,我们先规定一个池化核(Pooling Kernel),然后规定它的步长,一般步长和池化核大小一致,次数我们选用2*2的池化核,步长为2。
· 注意!池化层一般是不做Padding的,因为池化的意义就在于去掉relu后大量的0,再补0是没有意义的!
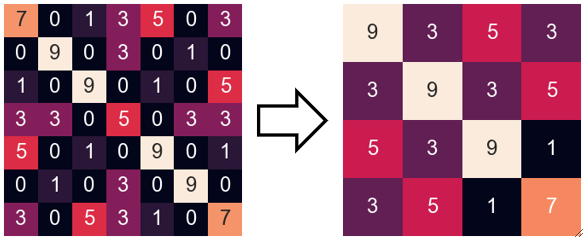
· 池化有最大池化(Max Pooling)和平均池化(Average Pooling),此处我们使用最大池化为例。
· 然后我们像移动卷积核一样移动池化核,但是只是取核中最大的那个元素作为结果:

· 而平均池化就是取均值:
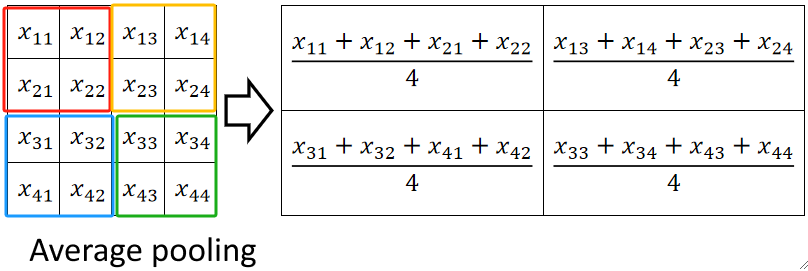
· 值得注意的是,任何减少计算量的行为都会导致精度的下降,这就像一个天平,因此池化操作不是很保险~
· 同理,输出结果也是可以通过公式计算出来的,公式如下,一般P=0,K=S=2:
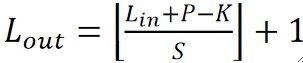
· 我们来看个例子,对上面relu后的结果做池化就变成了下面,可以发现,虽然0都被去除了,但是原来找到的四个特征(4个9)只剩下了3个,所以精度损失了一点。
前向传播总结
· 至此,前向传播就基本完成了,我们可以总结为卷积层、ReLU层、池化层,全连接层:
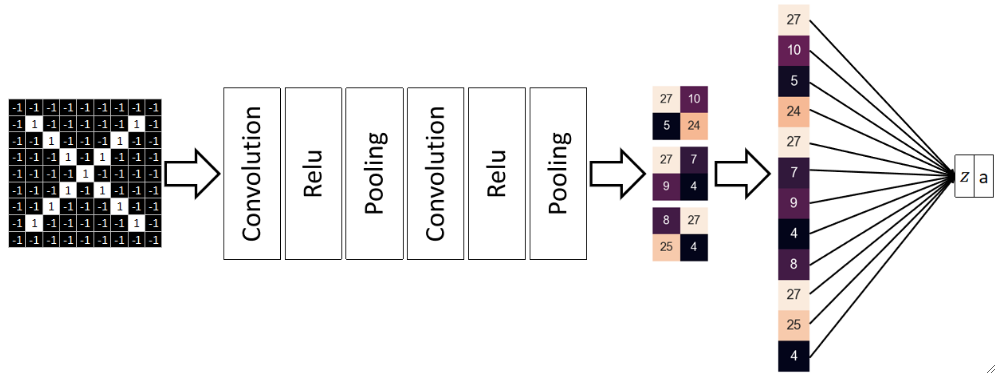
· 可以发现,我们把池化层的结果拉平了,拉平后通过一个简单的线性函数就可以算出z,然后根据要求,使用Sigmoid或Softmax来转换成概率a即可。
· 其实最后全连接层就相当于过了一次逻辑回归或者其它什么算法,只不过输入的数据不再是人为给的,而是CNN帮我们提取出来的。
· 所以不要忘记,无论是CNN还是普通的NN,它都只是一个特征提取器(Feature Extractor)罢了,真正完成任务的还得靠我们的其他算法。
· 上图展示的结构就是最简单版本的LeNet。
损失函数
· 因为我们要做的是多分类,那损失函数必然是选择交叉熵损失函数了。
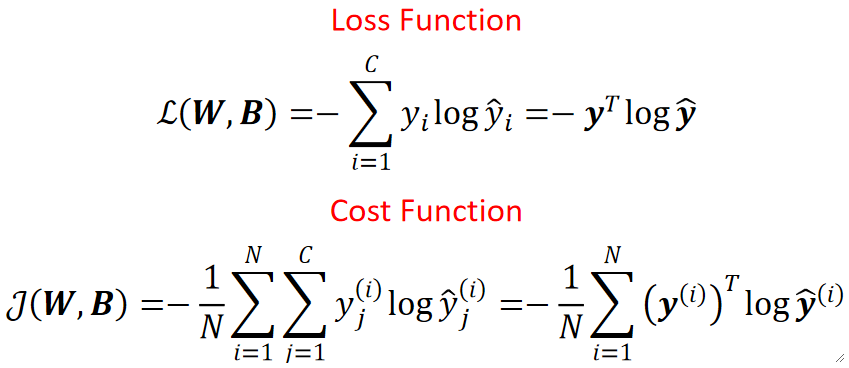
反向传播
Step 1
· 我们从损失函数开始反向传播。
· 首先,损失函数是L=-y^Tlog\widehat{y},求偏L偏y hat的过程我们已经在神经网络求过,这里直接给出结果为:
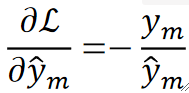
Step 2
· 再往前一步,就是神经网络的输出经过了Softmax转为了概率,即\widehat{y}=a=softmax(z),它的反向传播我们也求过了,z的个数就是我们类别的个数,直接给出结果为:
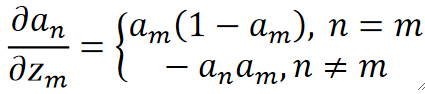
Step 1+2
· 然后我们可以把这两步揉在一起,首先,正向的合一起就是带进去就好:
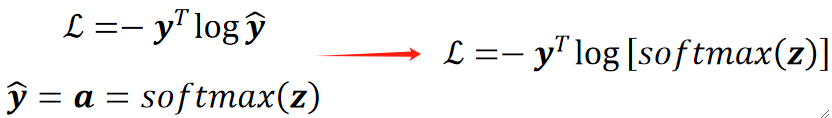
· 反向的合一起之后就跟n没有关系了:
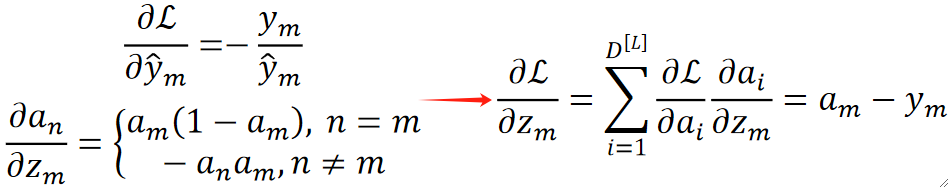
Step 3
· 再往前就是由全连接层得到的z,z就是通过线性函数z=(w)^Tx+b得到的,那么求偏z偏x就很好求了,就是对应的权重w:
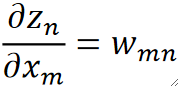
· 那么求偏L偏x就好求了,就是用之前反向传播回来的偏L偏z乘偏z偏x,就是w即可:
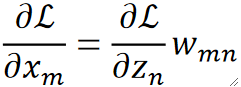
· 到了这一步,我们除了继续往前传播之外,还要更新参数w和b了。
· 那就是要计算偏L偏w和偏L偏b,这个我们之前也求过,先计算偏z偏w和偏z偏b,然后再算两个参数的偏导,最后结果中的偏L偏z就是上一层传过来的东西,最终得到:
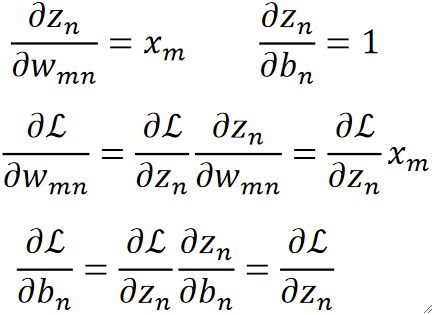
Step 4
· 再往前走就是池化层了,它负责输出我们的x。
· 由于标号不够用,从这里开始重新定义一下标号,这里的z就是池化结果,即送到全连接里去的x;这里的x就是上一层ReLU送进来的值。
· 我们上面用到的池化是最大池化,也就是选池化核内最大的那个值。
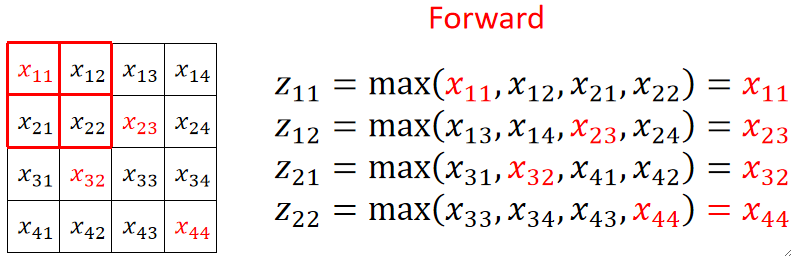
· 可以发现,求偏z偏某一个x的时候,如果是被选上的那个x,那结果就是1,否则就是0:
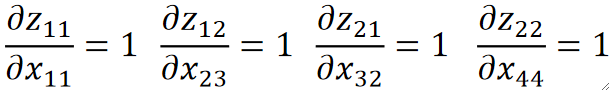
· 那么反向传播的时候,我们要求偏L偏某个x,就是就是求dL/dz再dz/dx,因为我们知道dz/dx不是1就是0,所以只有被选上的x对应的dL/dx有值,其它x对应的都是0:
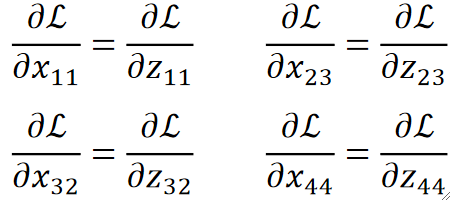
· 实际编程实现的时候,我们需要在正向传播的时候就把最大值的位置记录下来,形成一个这样的矩阵:
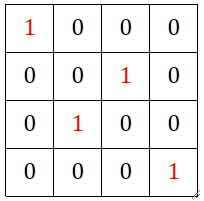
· 然后把反向传播回来的4个dL/dz(注意这个z是全连接层的输入x),分别和四个池化核框住的小矩阵相乘,得到的就是四个dL/dx:
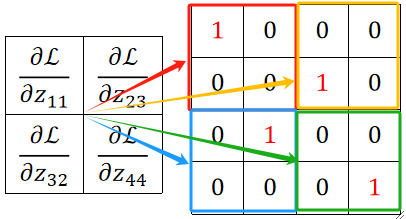
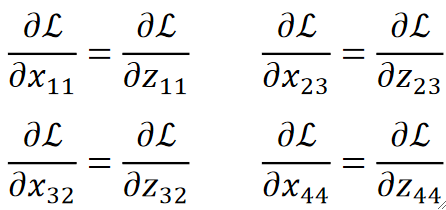
Step 5
· 再往前一步就是ReLU层了。
· 我们知道ReLU只是把小于0的置0了,即z=relu(x)=max(0,x),那求dz/dx其实也是分是不是0来讨论即可:
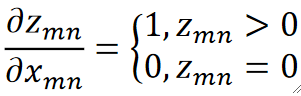
· 所以求dL/dx也很简单了:
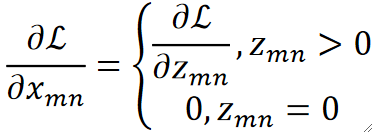
· 举个例子,假设经过ReLU前后的矩阵如下:
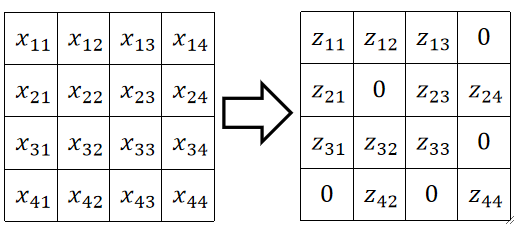
· 那我们只需要记录一个与其对应的dz/dx的矩阵:
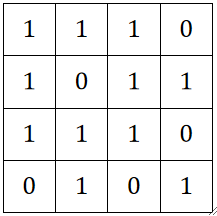
· 然后拿池化层反向传播回来的结果与其直接点乘即可:
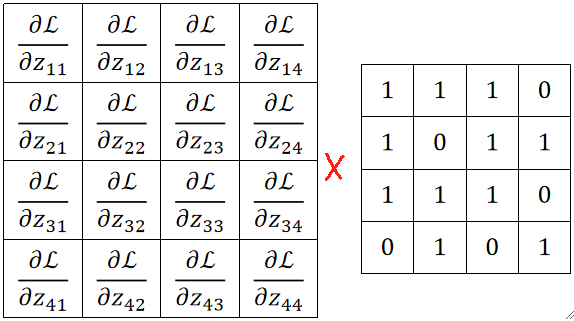
Step 6
· 先抛出一个例子,原图4*4,卷积核2*2,偏置3*3。
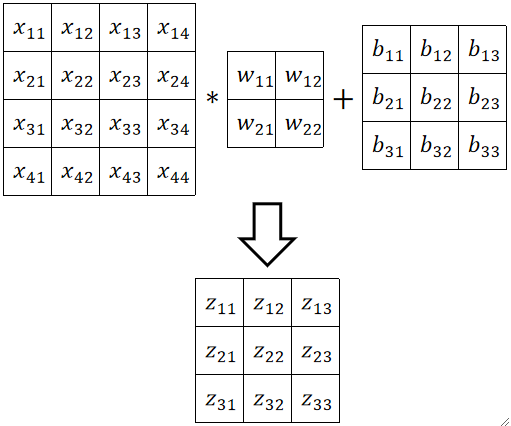
· 计算过程为:
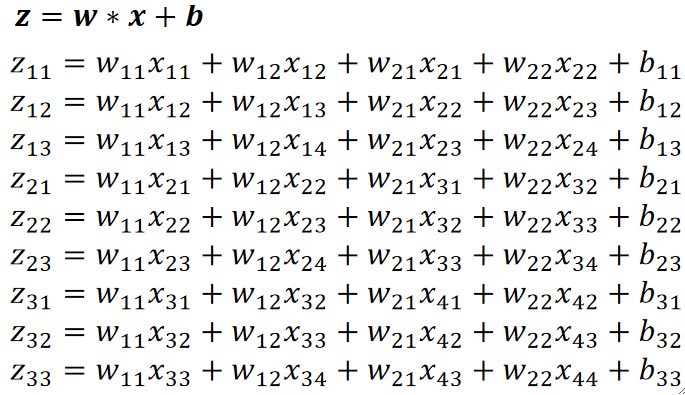
· 要计算dz/dw的话,可以发现,看上去基本上没什么规律。
· 算dL/db的话还好一点,算比较好求,dL/dz就是反向传播回来的:
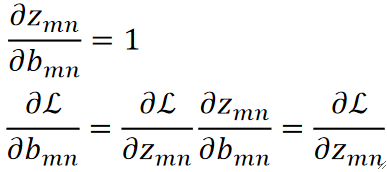
· 如果要求dL/dw的话就难搞了,因为每个w都跟所有的z有关,其中dL/dz是反向传播回来的:
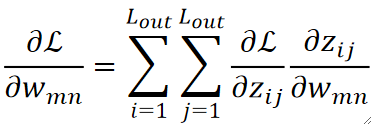
· 但是dz/dw就难搞,他跟x到底有什么规律呢?
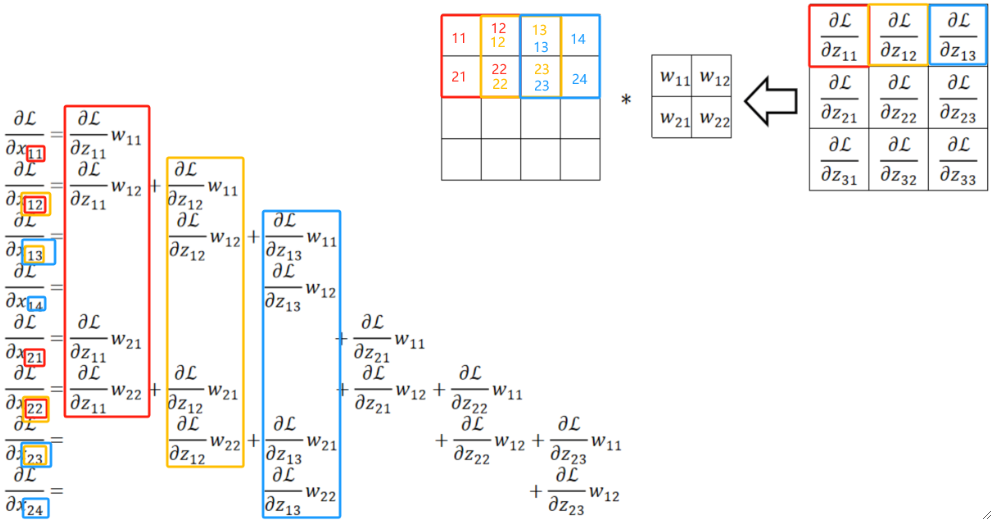
· 我们不妨把dz/d每一个w都写出来看看:
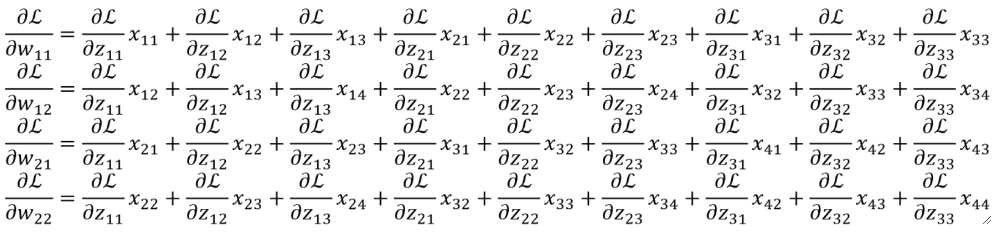
· 首先我们横着看,其实每一个式子就是把传回来的dL/dz当做“卷积核”和原图做“卷积”:
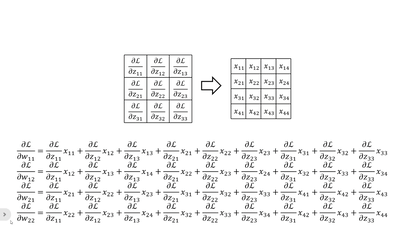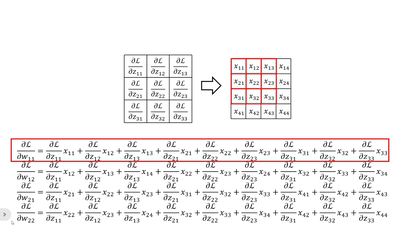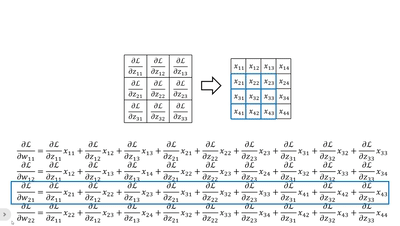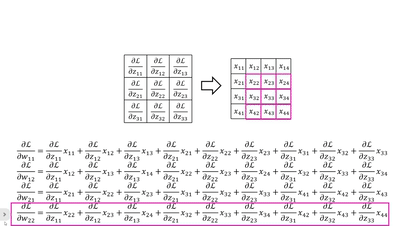
· 当然,我们还可以竖着看,这个比较复杂,首先我们拿原来卷积核的大小套上去,然后拿回传的一个个dL/dz广播乘,就是每一列的结果:
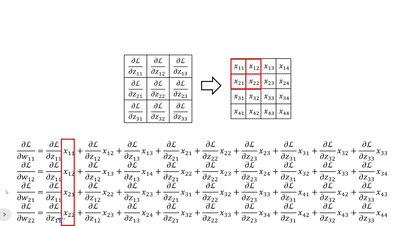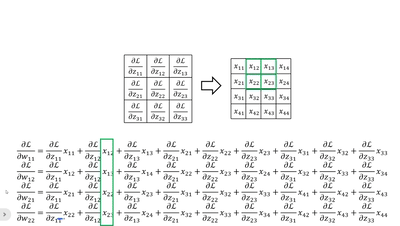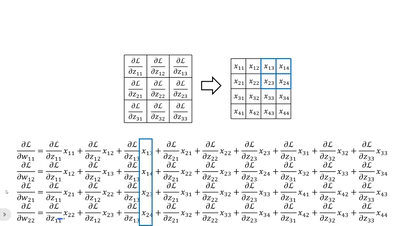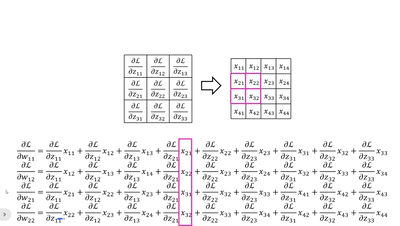
· 这样子我们就可以更新w参数了~。对于b来说就是一一对应即可。
Step 7 (可选)
· 如果在卷积层的参数更新完之后,还要往前继续传播的话(不止一次卷积ReLU池化),就要把dL/dx继续求出来往前传了。
· 我们也是不妨把求解过程都写出来看看:
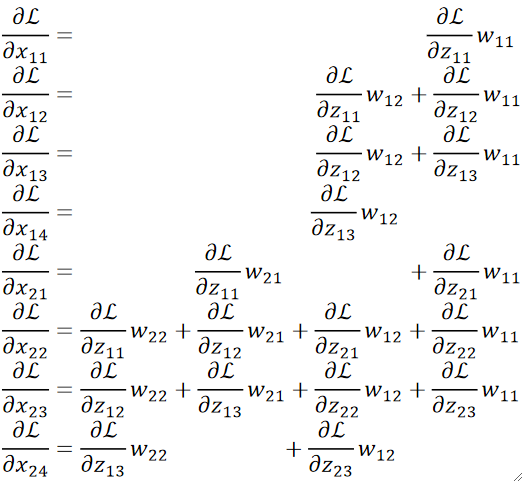
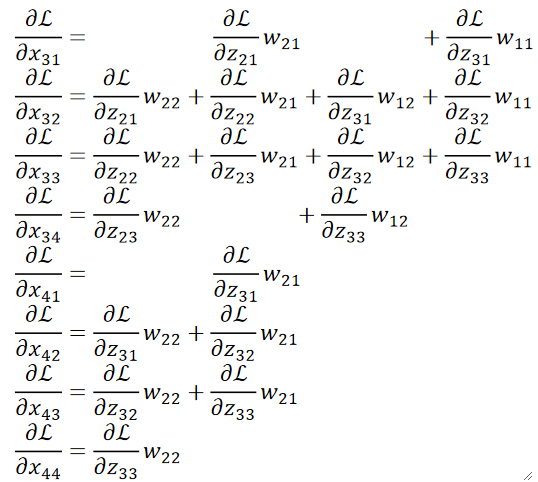
· 首先,我们横着看,规律其实非常有趣,首先,我们把反向传播回来的矩阵在外面Padding一圈0:
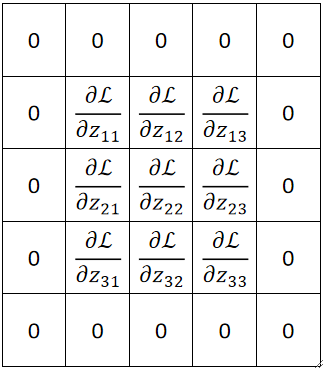
· 然后,我们把原来的卷积核转180度:
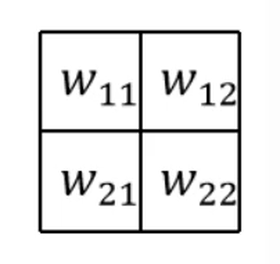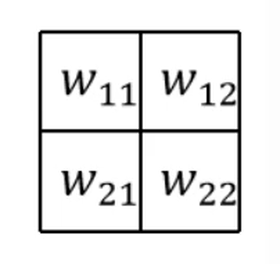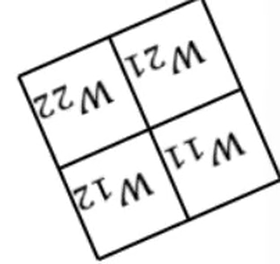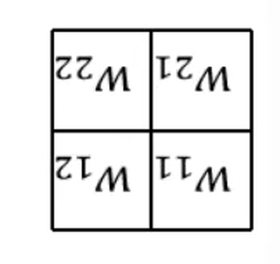
· 然后拿翻转后的卷积核去和加了一圈0的反向传播的结果做卷积,得到的就是我们想要的dL/dx:

· 然后,我们竖着看,能发现另一种规律。
· 拿反向传播回来的结果一个一个广播乘卷积核,然后放到对应的原图位置上去,然后把所有结果累加起来,就是最终的结果。
· 至此,反向传播全部完成。
多通道情况下的卷积与池化处理
前向传播
· 我们刚刚讲的所有操作都是基于输入图片只有一个通道(灰度图)。
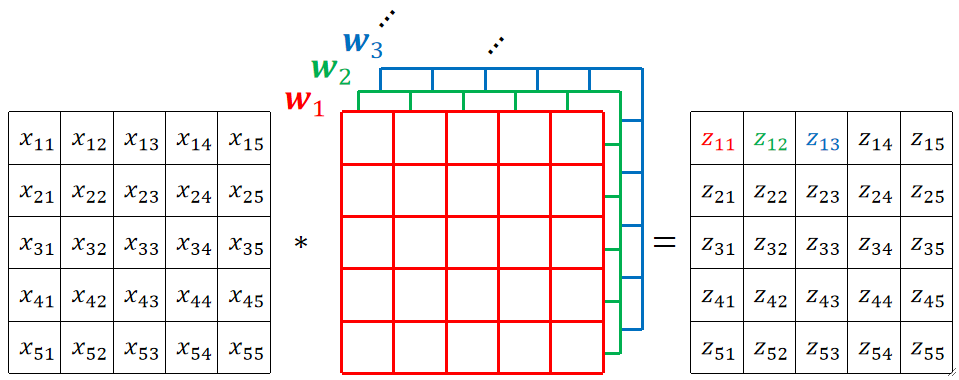
· 假设我们有三个卷积核,经过一次卷积,ReLU和池化后得到了3张4*4的图,我们把这个提取完特征后的图像称为特征图。
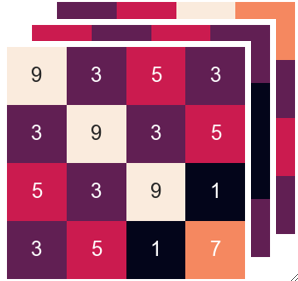
· 可以发现,我们现在从原来的一个通道变成了三个通道,也就是说,这一层的输入通道数是由上一层的卷积核数量决定的。
· 如果是这样的话,我们要再进行一次卷积操作的话,卷积核就要发生变化了。
· 很明显,卷积核的通道数要和输入的通道数相匹配,也就是3。这样,每一个卷积核的每一个·通道有4个参数,那么一个卷积核,3个通道,就有4*3=12个参数!
· 当一个卷积核进行卷积的时候,每次都有12个值,把12个值加起来,再加上偏置b,就是最后输出的一个值:
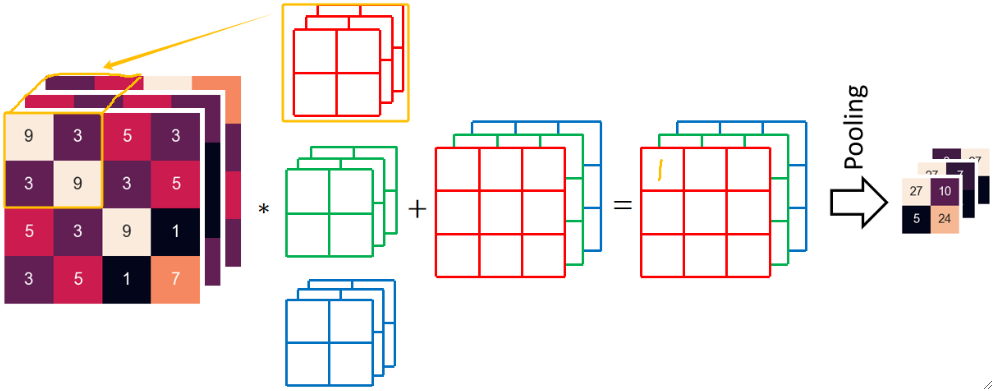
· 这样走完9次之后,红色卷积核就能卷出来最后红色的3*3结果。同理,绿色和蓝色卷积核一样操作,就可以得到绿色和蓝色的3*3结果。
· 最终组合出3*3*3的结果再ReLU和Pooling,就是最终结果。
· 可以发现,最终输出结果的通道数和卷积核的个数是相匹配的。也就是说,如果我的卷积核数量是4,那最后输出的结果应该是4*3*3。
反向传播
· 首先,因为我们有三个通道,那反向传播回来就有3个结果,下标的前两个数字就是位置,最后一个就代表输出的第几个通道。
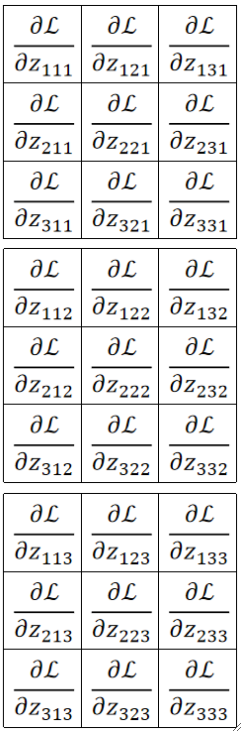
· 在这个例子中,我们输入的通道数是2,卷积核数量是3,卷积核通道为2,故输出的通道数是3。
· 在更新参数b的时候,直接dL/db=dL/dz即可,一一对应的。
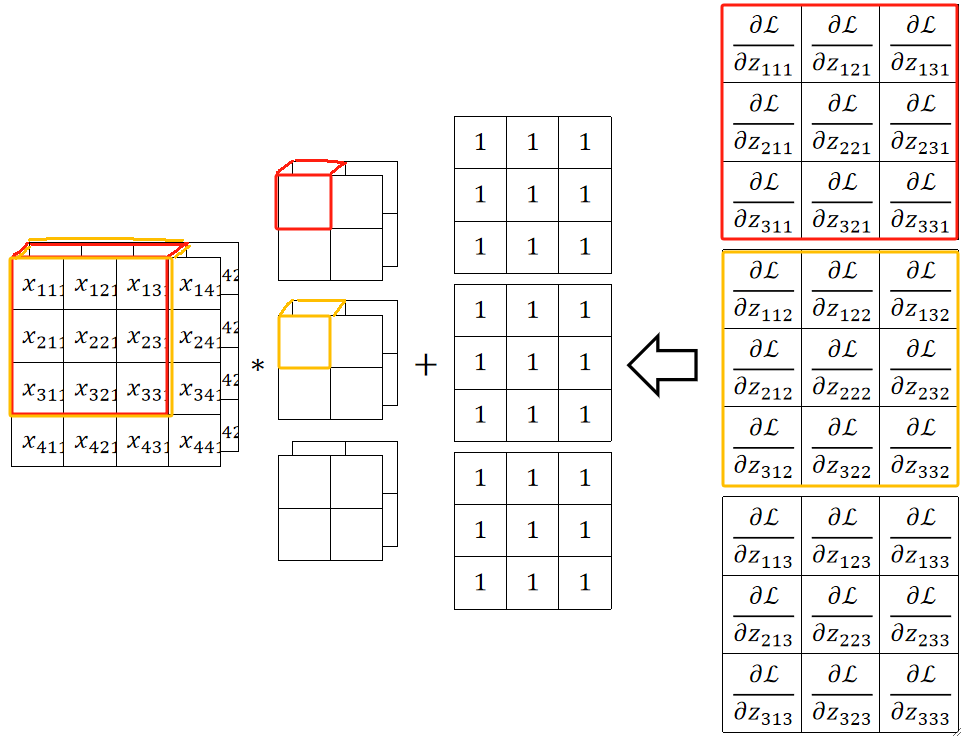
· 在更新参数w的时候,和前面一样,把传回来的结果当做卷积核去卷即可。需要注意的是,通过广播乘的方法可以更快一点。这是横着看的规律,竖着看的这里就不讲了。
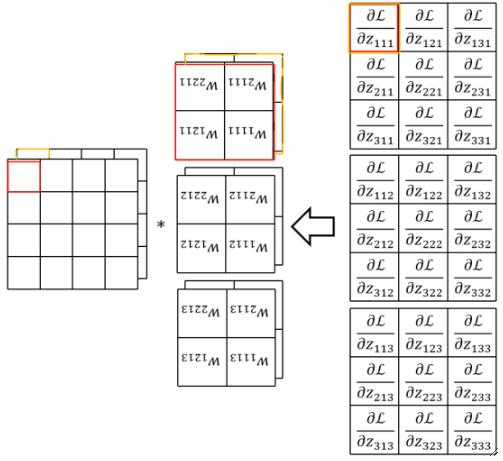
· 如果要继续反向传播回去的话,也就是要求dL/dx了,其实也是类似的,先给回传结果补0(这里不画出来了),然后拿翻转后的卷积核去卷补0后的结果:
总结
· 基本上CNN就差不多了。但还需要注意几个点
如果在做卷积之前考虑Padding的话,其实后续操作都是一样的,只是当成图片大了一点而已。
我们讲的都是一个样本,所以是dL,但实际情况是多个样本,所以要考虑的是dJ:
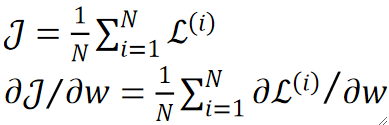
可以使用Image to Column来加速卷积操作,可以把卷积操作变成矩阵乘法,来加速我们的计算速度。
· 假设我们的样本是2*4*4的,然后需要3个卷积核来卷,即3*2*2,其实可以先把卷积核拉直,变成1个3列8行的矩阵:
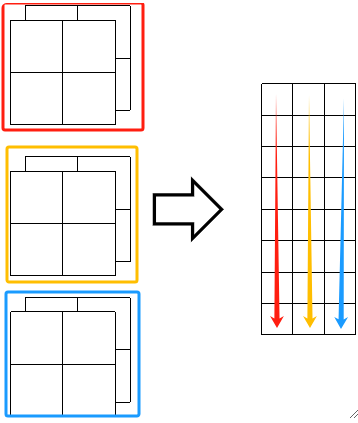
· 然后我们再把原图也拉直为一个矩阵,注意要和卷积核的顺序对应:
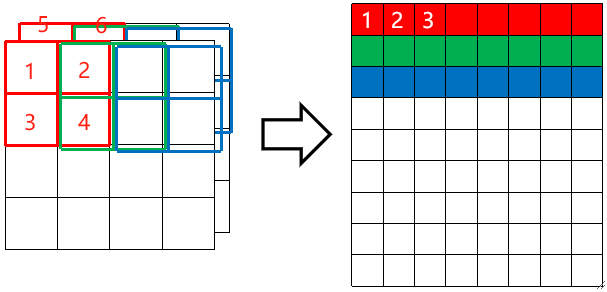
· 然后我们把这两个变换后的矩阵直接做矩阵乘法,即9*8的矩阵乘8*3的矩阵,得到的就是9*3的结果,然后再按顺序变回来就是3*3的结果了。
· 当然,这种变法是把输入特征图打乱,还有另一种变法是把卷积核打乱,但思想上是差不多的,此处不做解释了。
