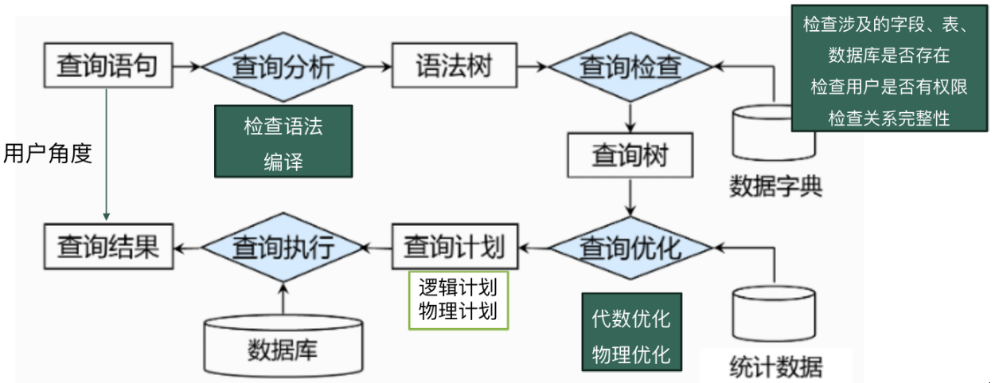
查询在DBMS中如何执行?
· 在用户的角度,我们把一个查询语句发给DBMS,那我们就能拿到查询结果。
· 在系统角度,它会做很多事情:
查询分析:对我们输入的SQL进行语法检查,并编译为语法树。
查询检查:使用数据字典进行查询检查,检查涉及的字段、表和数据库是否存在,
检查用户权限、关系完整性,生成查询树。
查询优化:使用统计数据对查询进行优化,如代数优化、物理优化,然后生成查询计划,
包含物理计划与逻辑计划。
查询执行:根据查询计划使用数据库进行查询,并返回结果。
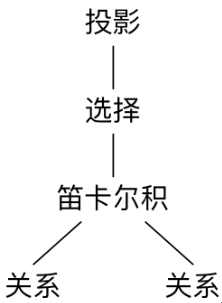
查询树
· 在查询检查后生成的查询树是什么呢?
· 查询树是关系代数在DBMS中的表示形式。它的格式是这样的:
· 举个例子,选出Student表中所有Sage小于19的学生的Sname,则查询树可表示为:
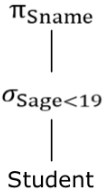
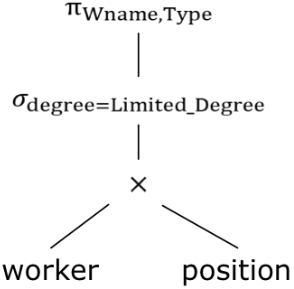
· 再看一个例子,等值连接woker表的degree和position表的Limited_Degree之后选出所有的Wname和Type用关系代数可表示为\pi_{Wname, Type} (worker \bowtie_{degree=Limited\_Degree} position),那么其查询树可表示为:
· 此时我们来回忆一下查询语句的执行顺序:
先从FROM构造查询关系,即笛卡尔积。
扫描关系,根据WHERE的条件把符合条件的元组保留下来。
根据SELECT把有需要的列筛选出来生成查询结果。
· 是不是和查询树自底向上的顺序一模一样?
查询优化
· 在获得了查询树之后,查询优化器会利用一些统计数据去生成很多种不同的执行计划,然后估算这些计划的代价,然后选择最优计划。
· 这些统计数据包含了元组信息(元组总数、长度、占用块数),列信息(值的格式,最大最小值,有无索引,索引类型),索引信息(索引个数,基数,参数)。
· 那么代价(开销)如何计算呢?我们有一个代价模型:
总代价 = I/O代价 + CPU代价 + 内存代价 (+通信代价)
· 其中,I/O代价指的是磁盘存取的块数,块数是文件存取的最小单位,一般为4KB。
· CPU代价指的是处理指令需要的时间,需要转换成I/O代价来计算。
· 内存代价和数据库的缓冲区大小有关。
· 通信代价只有分布式数据库才有。
· 我们主要关心I/O代价,我们来看看如何计算。
· 首先我们需要知道,数据都是存储在硬盘上的,需要读到内存中才能进行操作。那么I/O代价就是算需要从磁盘上拿多少块到内存中。
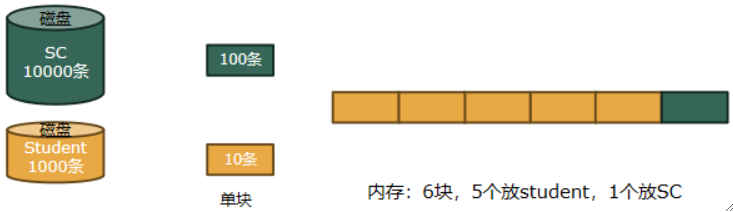
· 举个例子,如下图,磁盘中存储了1000条学生数据,磁盘中一块能存50条,而划分给数据库的内存缓冲区只有10块:

首先,我们计算存取所有数据需要用到:1000 / 50 = 20块。
然后我们对比缓冲给的10块,发现一次读不完,需要分批读。
单表查询计划
· 接下来通过一个例子来对比查询计划。假设我要执行\pi_{Sname}(\sigma_{Sage<19}(Student)) 这条查询。
· 查询计划①——选择操作的全表扫描。
· 如果没有索引,则进行全表扫描,并丢弃Sage>=19的行。
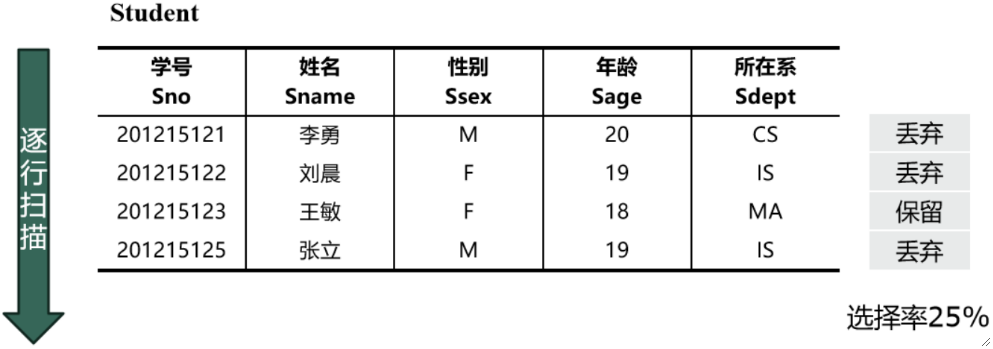
· 不难发现,全表扫描法虽然控制简单,但是选择率很低,因此适合小表的查询。
· 我们来计算一下这个查询计划的代价。其实就是我们刚刚举的例子,1000条/50条每块,因此需要20块,而缓冲区只有10块,因此需要分两次进行处理。
· 查询计划②——选择操作的索引扫描。
· 如何Sage这个属性上定义了索引,则可以直接通过索引定位到Sage<19的行。
· 有顺序的数字我们一般都使用B+树索引,其根结点是一个中位数,每个节点的左子树都比它小,右子树都比它大。
· 因此我们可以从根节点向下搜索到Sage=19的节结点,然后找到它的左子树,用地址找到对应的行进行输出。
· 得益于B+树的特性,索引扫描法非常高效、快速,但如果目标元组分布均匀,那效率肯定是不如全表扫描的。其次,定义索引需要消耗额外的内存,因为是先找索引再找表,所以最终代价还需要加上找索引的搜索代价。
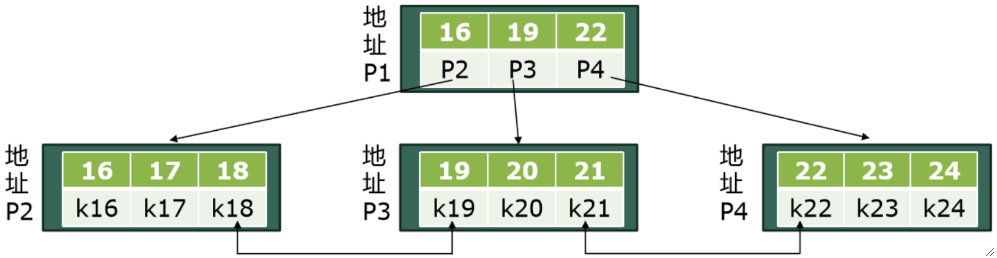
· MySQL中使用B+树存储索引的方式如下:
① 如果不是叶子节点,就存索引数据以及子节点的地址,如下图的地址P1。
② 如果是叶子节点,但索引不是主键,则存对应的主键,如下图的P2-4。因此非主键索引查询还需要加上根据主键找具体元组这一步。
③ 如果是叶子节点,且索引是主键,则直接存对应的元组,即一整行的数据,如下图中的P2-4。
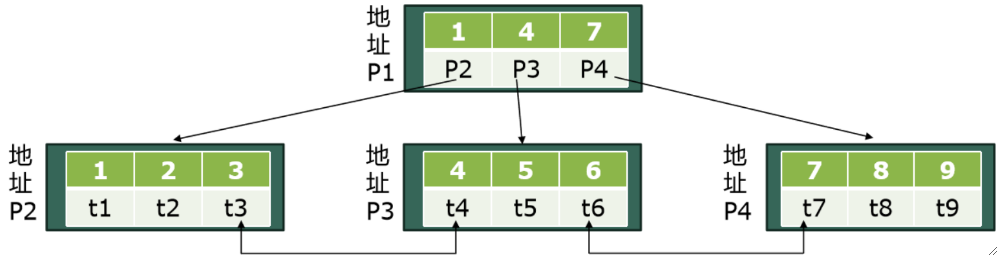
· 综上所述,在主键上建立索引,并对主键进行筛选的速度是最快的。
· 我们来计算一下这个计划的代价。因为一个数对于一个节点来说不是大于、小于就是等于,每个结点消耗1块,因此每一层只需要1块,故有多少层就需要多少块来查询索引,然后加上符合条件的元组消耗的块数。
· 举个例子,假设B+树有3层,最终会查出300条符合条件的元组,1块可存50条,则共消耗3+300/50=9块。
· 最坏条件下,所有数据都符合条件,以1000条为例,则消耗3+1000/50=23块,比直接全表扫描还多。
· 对比两个查询计划:DBMS在创建索引的时候会统计一些分布信息从而对查询进行预测,当年龄已创建索引且符合条件的元组不多的时候会选择索引扫描,否则全表。
多表查询计划
· 连接的查询计划实现有以下四种方法:
嵌套循环:最简单可行。对于左表的每一个元组,需要遍历右表中的每一个元组,找到满足条件的结果输出。

归并排序:基于两张表都已经按连接条件排好序的情况。因为已经排序,所以当遇到第一个不相等的时候就
直接break本层遍历即可,后面的肯定不相等。
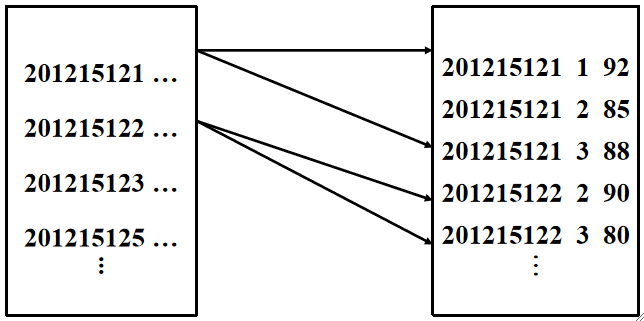
索引连接:基于内层表连接条件的属性上有索引的情况。
哈希连接:在等值连接时把连接属性作为哈希码(Hash Code)。
· 对于多表查询,我们需要计算笛卡尔积的代价,因为无论是上述哪一种连接都需要计算笛卡尔积嘛,接下来看看如何计算。
· 首先,假设我们磁盘里有1000条Worker数据,20条Position数据,Worker等值连接Position;一块可以读出50条Worker数据或10条Position数据,主缓冲区一次总共可读出10块;现在聪明的DBMS通过计算得出每次读9块Worker,1块Position,那么计算过程如下。
① 计算要读多少块才能读完Worker:1000 / 50 = 20块。
② 计算要读多少块才能读完Position:20 / 10 = 2块。
③ 接下来我们读第一次,根据规则,9块Worker和1块Position,那就如下,花费10块:

④ 很明显,Position要读2次才能读完,因此根据嵌套循环的规则,第二次读的如下,花费1块:

⑤ 现在w1-w9都和Position比较完了,也就是第一次外层循环执行完成,现在要执行第二次外层循环,和第一次一样,共花费11块:
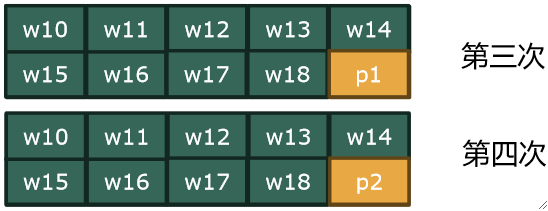
⑥ 现在w1-w18都和Position比较完了,但是w19和w20还没有,别忘了他们,还得加上4块:

⑦ 到此,Worker表与Position表比较完成,共花费11+11+4=26块。
· 接下来我们用更简单的方法再算一个例子:
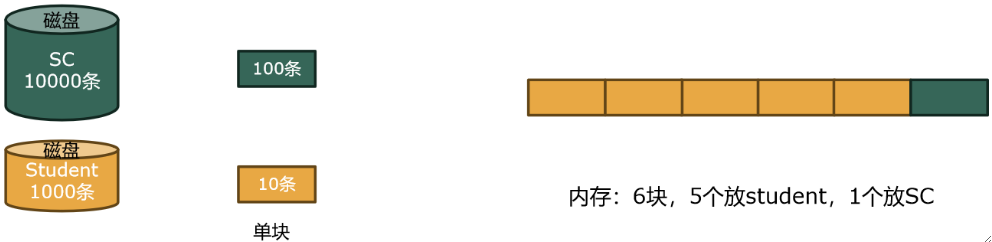
① 根据主内存缓冲区给出的数据,每10*5=50条Student需要换10000 / 100 = 100块绿色才能遍历完。
② 如果需要把Student都遍历完,需要替换1000 / 50 = 20组。
③ 每组要读100块绿色,所以绿色要读20*100=2000块,黄色只遍历了一次,读1000 / 10 = 100块。
④ 故最终结果为2000+100=2100块。
· 那么使用这个方法如何计算我们一开始的例子呢?
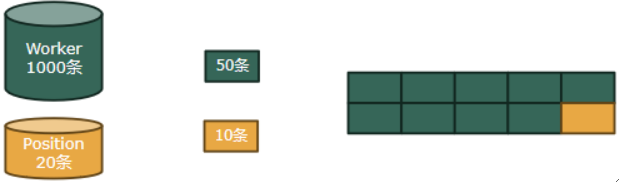
① 主内存中每50*9=450条Worker需要换20 / 10 = 2块Position才能遍历完。
② 如果要把Worker遍历完,需要替换1000 / 450 = 2.22组,除不尽的时候我们向上取整,即3。
③ 每组要读2块Position,故黄色要读3*2=6块,绿色只遍历了一次,即1000 / 50 = 20块。
④ 故总共需要20+6=26块。
· 接下来我们再算一个例子:
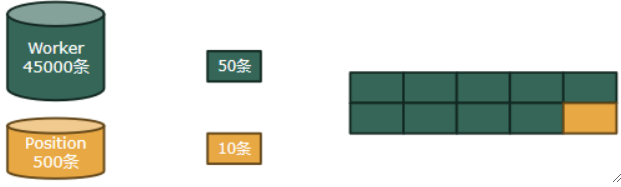
① 主内存中50*9=450条绿色需要500/10=50块黄色才能遍历完。
② 如果要把绿色遍历完,需要替换45000/450=100组。
③ 每组要读50块黄色,因此黄色要读100*50=5000块,绿色只遍历了一次,就是45000/50=900块。
④ 故总共需要5000+900=5900块。
· 做了那么多例子,我们就能总结出一条普遍适用的公式了,假设小表有N条数据,大表有M条数据,每块能读小表n条,大表m条,主内存最多能存放A块,则最终需要的块数为:

· 接下来我们对比一下,对于同一条关系代数,不同的执行计划差异能有多大?
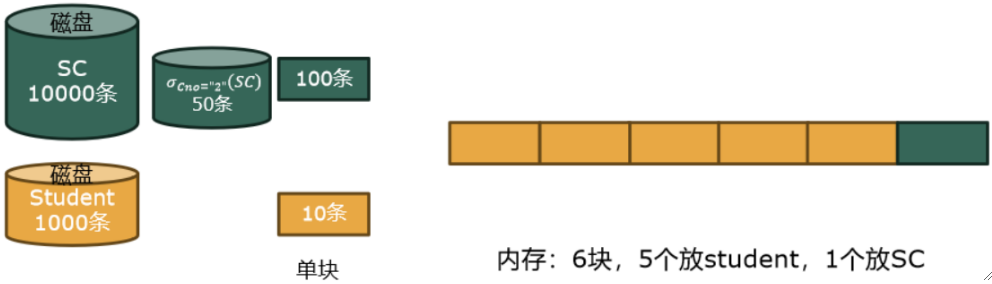
· 假设我们有数据库如下:
· 假设我们要对上面的数据库执行下面这一句SQL:
SELECT Student.Sname
FROM Student, SC
WHERE Student.Sno = SC.Sno AND SC.Cno='2';· 对于这句SQL,,我们可以写出下面三种查询计划:

· 查询计划① —— 笛卡尔积再选择。
① 前面我们知道,这个例子的笛卡尔积I/O代价是2100块。
② 笛卡尔积之后的元组数量是10^4*10^3=10^7。
③ 我们假设现在每个单块只能装入10条组合后的新元组,则共需要写入磁盘10^7 \div 10 = 10^6块。
④ 然后我们还要对笛卡尔积之后的结果进行筛选,如果是全表扫描,还要再把这10^6块再读一次。
最后总代价为2100+10^6+10^6块,这也太大了。
· 查询计划② —— 自然连接再筛选。
① 进行自然连接后,新关系的元组数量是10^4,对比原来少了三个数量级。
② 还是一块只能装10条新数据,则写入磁盘10^4 \div 10 = 10^3块。
③ 对自然连接的结果进行筛选,则全表扫描要读入10^3块。
最后总代价是2100+10^3+10^3块,是原来的488分之一。
· 查询计划③ —— 筛选再自然连接。
① 首先,先对SC进行筛选,如果是全表扫描,则代价为10000/100=100块,假设筛选后只有50条符合要求。
② 此时,SC筛选完的结果就直接在内存缓冲区等着了,不用存中间文件,即不用进磁盘了,因为50条<100条(1块)。
③ 故连接的I/O代价只需要计算Student的1000/10=100块即可。
最后的总代价为100+100块,这个优化相当可观!
· 可见进行优化真的太有必要了,像上面这样调换操作顺序叫做代数优化,又叫逻辑优化。
· 除此之外,我们还能建立索引,这叫物理优化。
如何进行查询优化?
· 从前面的例子可以看出来,为了优化I/O代价,我们要尽可能让DBMS查的少,查的快!
① 查的少:减少表的规模;加入索引;不引入与查询无关的属性。
② 查的快:能同时解决的事情不要分两次,如能连接就不要笛卡尔积再筛选;多次使用的中间变量考虑用视图存储。
· 而DBMS内部是通过查询书来对查询进行优化的,我们来看看如何做到。
· 首先,当你拿到一条查询,先把它写成只有五种基本形式的关系代数的形式(投影、选择、并、差、笛卡尔积)。
· 举个例子,有一句查询选了课程号为2的课程的学生姓名的SQL:
SELECT `Sname`
FROM `Student`.`SC`
WHERE `Student`.`Sno` = `SC`.`Sno`
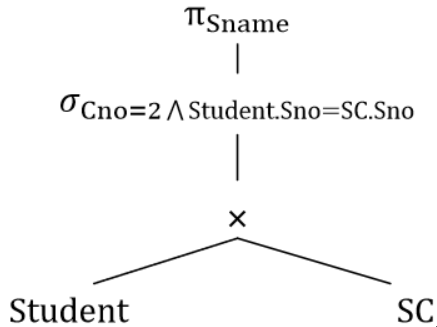
AND `Cno` = "2";· 那么写成关系代数的形式就是:\pi_{Sname}(\sigma_{Cno=2 \wedge Student.Sno=SC.Sno}(Student \times SC)) 。
· 然后,我们就可以按照投影-选择-笛卡尔积的顺序来写查询树,如:
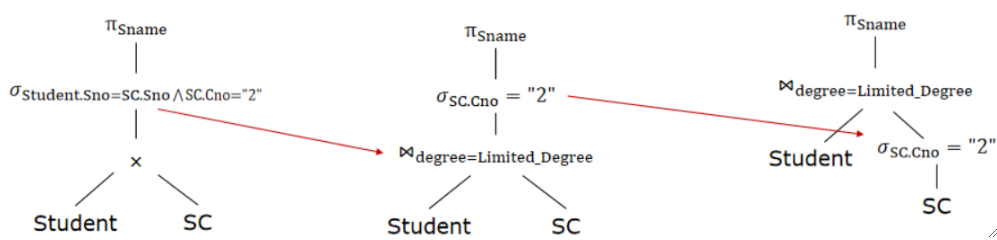
· 根据我们之前的查询计划,画出三棵对应的查询树:

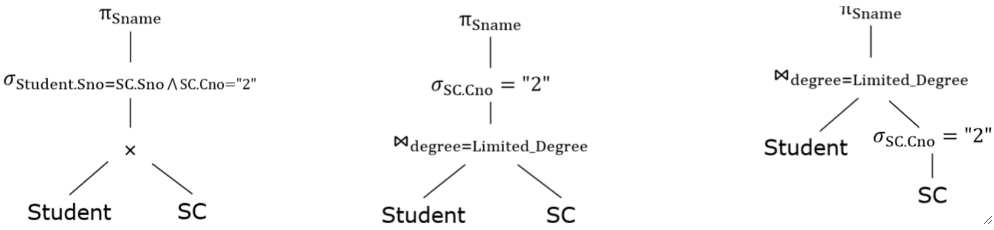
· 可以发现,每一次优化都是把查询谓词往下放了。
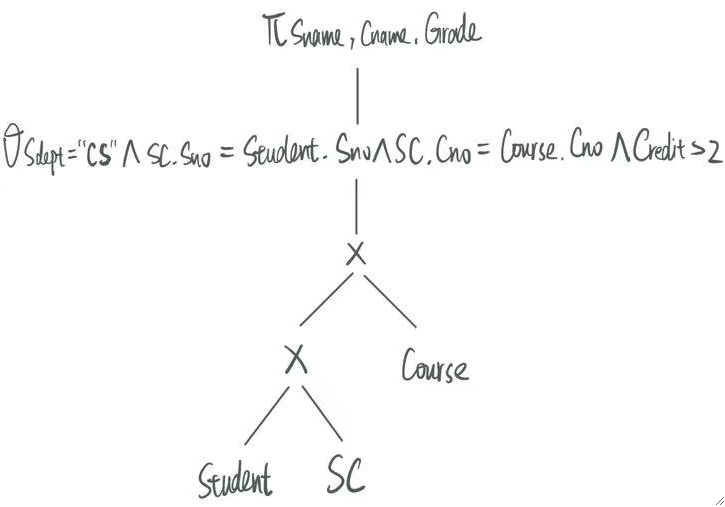
· 接下来我们通过一个例子来练习建立查询树与优化查询,首先给出表结构和一条SQL如下:

SELECT Sname, Cname, Grade
FROM Student, Course, SC
WHERE Credit > 2
AND SC.Sno = Student.Sno
AND SC.Cno = Course.Cno
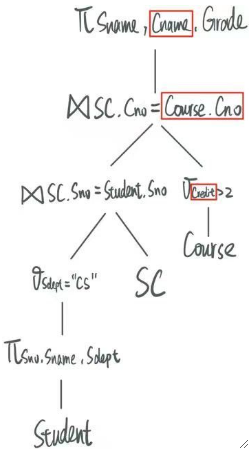
AND Sdept = "CS";· 然后我们可以建立出查询树如下:
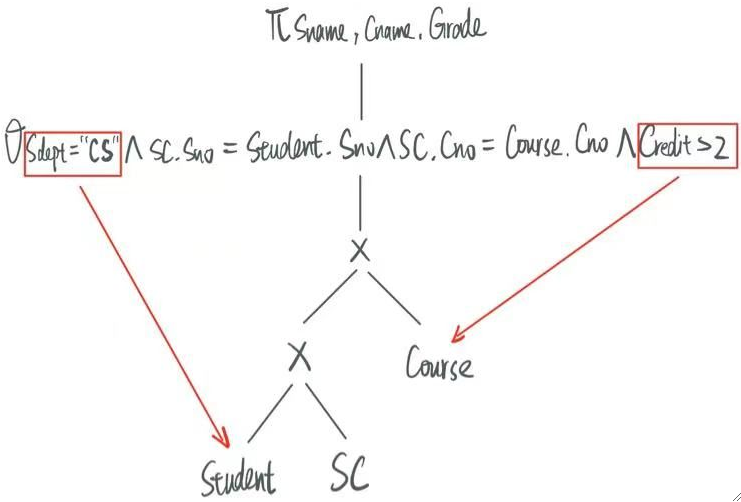
· 然后开始优化这个查询。
① 所有的筛选条件都往下移。
可以发现,Sdept和Credit的筛选都可以在连接之前完成,因此把它们往下移动可以优化查询时间。
移动完之后就得到了:
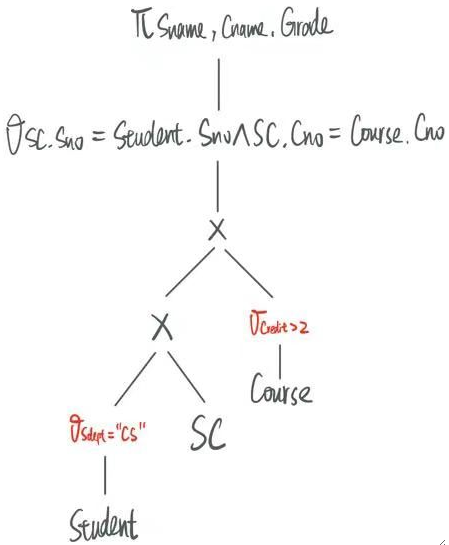
② 所有的连接条件都往下移。
可以发现,与其在把表自然连接完后做筛选,不如直接在连接的时候进行等值连接。
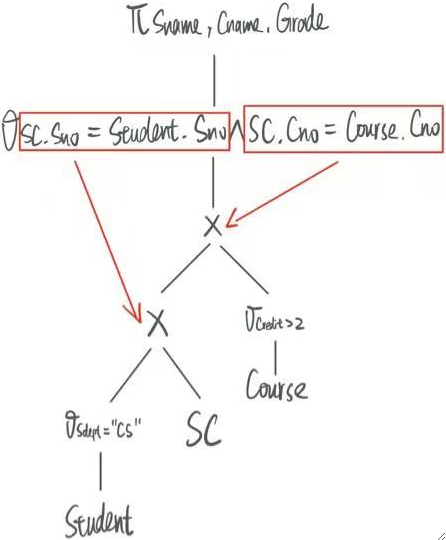
移动完后就变成了:
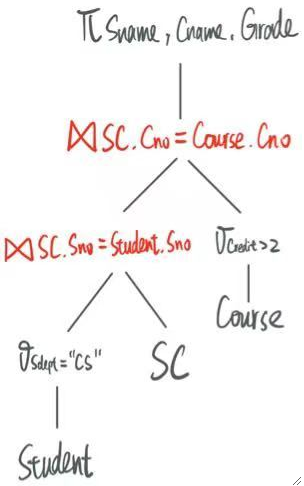
③ 选择有用的列。
可以发现,对于Student这张表,我们只需要用到其中的Sname,Sno和Sdept,其它列不需要用到,因此可以先把列拿出来,减少后续占用的内存。
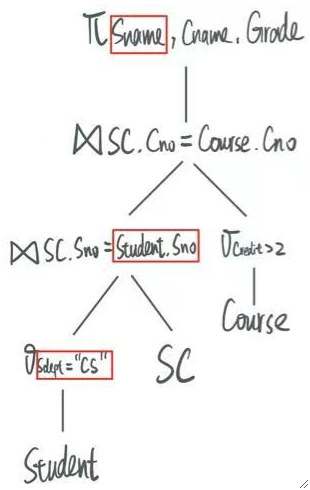
把需要用到的列拿出来之后就变成了:
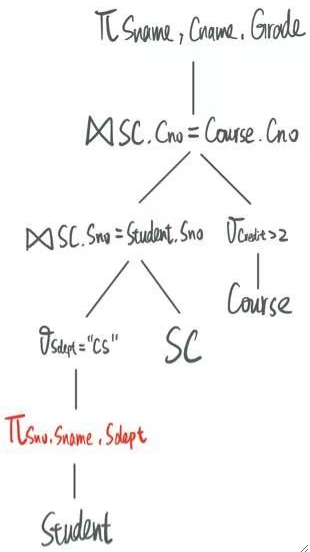
同理,对于Course这张表,我们只需要用到Cname、Cno和Credit。
· 提取完后就变成了:
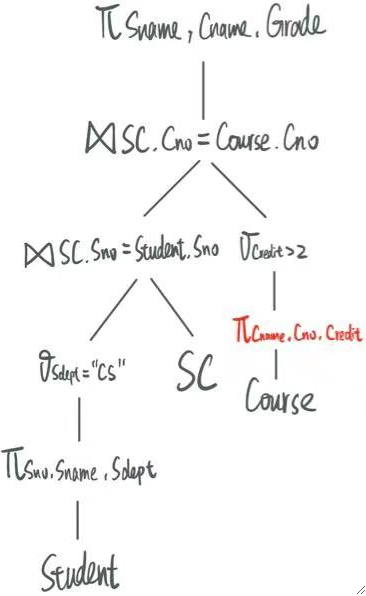
· 这样,就完成了查询的优化。这就是DBMS内部进行优化的原理。
· 尽管这些都是封装好在DBMS内部的,我们无法干预,但是明白这些原理之后,我们也可以依此来优化我们的SQL代码。
· 接下来介绍一些优化SQL代码的小手段。
① 避免使用 SELECT *
在表查询中,一律不要还有*作为查询的字段列表,需要用到的字段必须写明白!
其他人在读你的SQL的时候不用查表设计就能知道语句的输出是什么。
在对表的字段进行增加时,不会改变查询的结果。
减少空间的冗余,筛选无用的字段会增加I/O操作。
无法使用“覆盖索引”优化,效率低下。
PS:什么是覆盖索引?其实就是,如果你要筛选出来的列都是主键或索引,则称为覆盖索引,因为查询的时候不需要发生回表操作。
② 分页优化
在SELECT语句最后使用LIMIT来限定分页。
若LIMIT后只有一个参数n,则表示只显示前n个记录。
若有两个参数m,n,则表示从m+1行开始到m+n行的记录。
③ 小表驱动大表
通过小表去连接大表可以减少连接次数,从而加快查询速度。
一个直观的理解如下:

对于常用的谓词,我们可以利用该思想:
· IN:优先执行IN中的子查询,再执行外面的父查询。故IN中数据少的话查询会更快。
· LEFT JOIN:左边的表驱动右边的表,因此左边的表尽可能少比较好。
· RIGHT JOIN:右边的表驱动左边的表,因此右边的表尽可能少比较好。
· INNER JOIN:在MySQL中,它会自动选择小表来驱动大表,很聪明有木有!
④ 同义替换
IN和OR:优先使用IN,少使用OR,因为OR会容易让引擎进行全表扫描,放弃索引。
少用不等号,因为对于B+树索引,使用等值查询可以快速定位到某个节点,但是如果是范围查询则可能需要遍历多个节点。
子查询和JOIN:优先使用JOIN,因为子查询意味着建立和删除临时表,这会消耗额外性能。
对于一张超大表,我们可以考虑先分页再JOIN而不是整张去JOIN。
对于经常用的中间变量,可以考虑使用视图存储。
⑤ 物理优化:索引的建立和应用
索引尽量建立在那些将用于JOIN、WHERE和ORDER BY的字段上。
尽量不要对数据库中含有大量重复值的字段建立索引,没什么帮助。
索引的字段不能有NULL(废话)
MySQL中只会使用一个索引,如果WHERE子句使用了索引,那么ORDER BY就不会用。
如果排序包含多列的排序,最好构建复合索引。
特别的,对于LIKE语句,像”%aa%“这样的匹配不会使用索引,但是”aa%“则可是有索引。
