算术运算
· 图像的算术运算指的是对输入的两幅图像进行点对点的加减乘除运算,数学表达式如下:
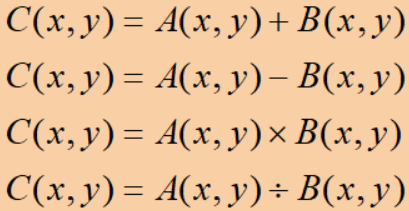
· 注意,算术运算是逐个像素进行的!图像的乘法/除法也是,并非是矩阵的乘法!!
加法运算应用
· 运用①——均值降噪,对同一场景的多幅图像求平均值,以降低叠加性随机噪声。
· 假设有一个噪声图像集如下,其中F为原图像,H为噪声,i为1,2,3,.....,M:
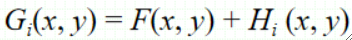
· 对M个图像求均值,即每一个像素点最后的值来自这M张图像的均值:
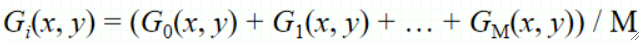
· 当噪声H互不相关,且最终求出的均值G为0时,求出的均值将降低噪声的影响。


· 另一个典型例子:当你想拍摄一个静态景物但周边会有游客走来走去的时候,只需要对着这个景物持续拍摄,最后求一个均值即可得到一个没有游客的纯景物图片。
· 另一个典型例子:手机拍摄夜景,一般会叫你保持不动连续拍摄多张,最后自动求均值以降噪。
· 运用②——二次曝光,将一幅图像的内容直接加到另一幅图像上。
· 假设有两幅图像AB,各取一半进行二次曝光则为:
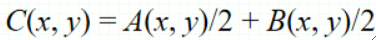
· 推广这个公式,可以通过控制α,来控制两张图片对最后合成的图片的贡献度:
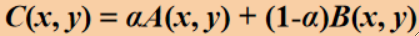
· 以下展示各取一半进行二次曝光的例子:

减法运算应用
· 运用①——减去背景,即去除不需要的叠加性图案。
· 假设有一副前景+背景混合图像A,另一幅只有背景的图像B,进行减法即可得到去除了背景的图像:
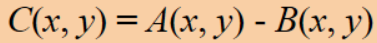
· 比如:

· 再比如:

· 运用②——运动检测,如果在同一位置隔一段时间拍两张照片,做减法,就能得到运动物体的图像,即差图像。
· 设时间1的图像为T1,时间2的为T2,则差图像为:
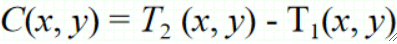
· 比如:

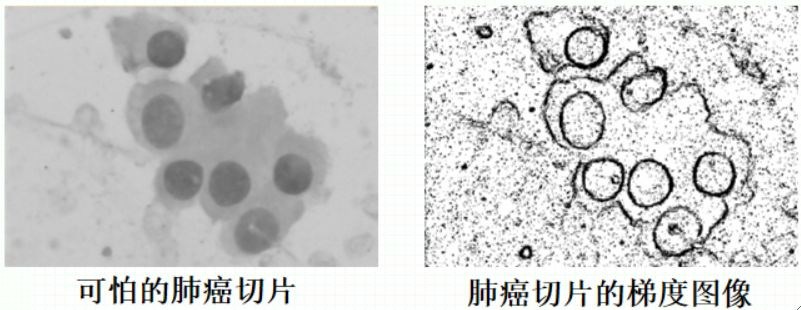
· 运用③——梯度幅度,通过计算图像每一点的斜率大小可以获得图像的梯度幅度。
· 连续的图像的梯度幅度计算公式如下:
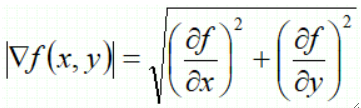
· 离散的公式如下,这是一个近似的公式,我们更常用这个,即计算当前点与自身右边、下边的像素点的差再加起来:
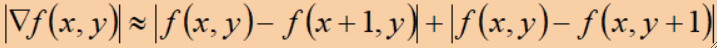
· 梯度幅度在物体边缘处很高,因为边缘的灰度变化特别大,而在均匀的内部很低。因此,梯度图像常用于轮廓特征提取。
乘法运算应用
· 运用①——二值蒙版,用二值蒙版图像与原图像进行乘法可实现图像的局部显示,即遮掉图像的某些部分。
· 首先,我们的自己设置一个蒙版,在需要保留下来的区域把蒙版值设为1,其他设为0,然后把蒙版与原图像相乘,即可得到局部图像。
· 例如:

· 运用②——“正片叠底”与“滤色”,前者模拟反光体的颜色混合,后者模拟发光体的颜色混合。
· 在胶片时代,如果晒出来的照片曝光过度,则只需要再晒一张,并叠在一起即可,因为胶片是反光体,叠在一起之后吸收的光增加,亮度就会下降;如果晒出来的照片曝光不足,可以使用发光体的原理,给胶片进行打光,类似把多张幻灯片叠加在一起。
· 正片叠底公式如下,两张图片A,B:
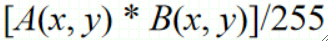
· 滤色公式如下,两张图片A,B:
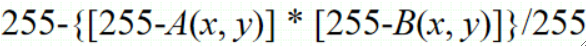
除法运算应用
· 除法运算可用于去除数字化器灵敏度随空间变化造成的影响,也被用于产生比率图像(对多光谱分析十分有用)。
逻辑运算
· 两幅输入图像进行点对点的与、或、异或计算而得到的输出图像,数学表达式如下:
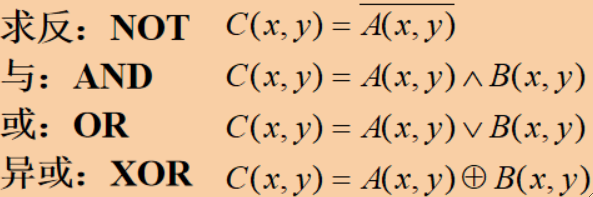
求反运算
· 定义:
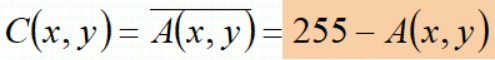
· 主要用于获得彩色图像的阴图像,即色调和灰度与被复制对象相反的图像;获得二值图像的补图像。
· 如:


与运算
· 定义,其中\land可以写成“·”:
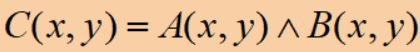
· 通常只用于二值图像,求两幅图像的相交子图:

或运算
· 定义,其中\lor可以写成“+”:
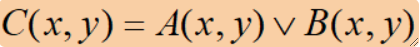
· 通常只用于二值图像,获得合并子图像:

异或运算
· 定义,即像素值相同取0,不同取1:
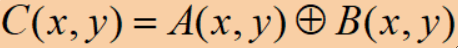
· 对于二值图像,常用于叠加(合并)两幅图像:

· 图像与自身异或即可删除该图像。
几何运算
· 几何运算可改变图像中各对象之间的空间关系,可以看成是物体在图像内运动。
· 几何运算需要两个独立算法:
① 描述运动:定义空间变换本身,描述每个像素如何从初始位置”移动“到终止位置,即每个像素的”运动“。
② 描述插值:需要一个灰度级插值的算法,因为很多情况下输入输出图像的像素点不是一一对应的,如放大。
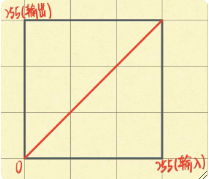
· 一般我们可以这样去描述一个几何运算:
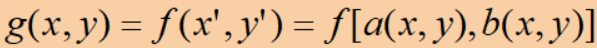
· 其中f(x,y)是输入图像,g(x,y)是输出图像,a(x,y)和b(x,y)唯一地描述了空间变换。
· 几何运算通常由两种映射方式实现:
① 向前映射法:输入坐标->输出坐标,适用于尺寸不变,无需插值的变换,如平移、镜像、转置。
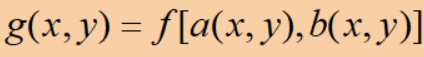
② 向后映射法:输出坐标->输出坐标,适用于尺寸改变,需要插值的变换,如缩放、旋转、拉伸。
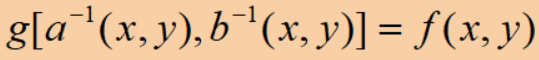
平移
· 因为输入图像与输出图像存在一一对应的关系,故不需要差值计算。
· 最简单的表示如下:
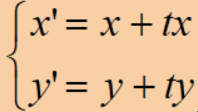
· 当然,我们更常用的是矩阵的形式:
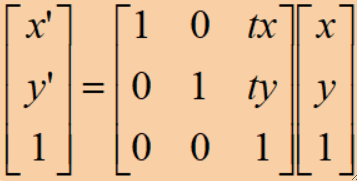
· 为什么矩阵会多了一维?是为了齐次,把投影等其它高级运算合并为一个矩阵,为这些高级运算做准备,但课程内不涉及。
· 为什么用矩阵表达?方便后续进行级联运算。
· 平移的例子:

· 如果不想在平移后改变图像大小,对于平移后不在输入图像中的点,可直接把它像素值设为0或255。
镜像变换
· 镜像变换也是输入输出一一对应,不需要差值计算。
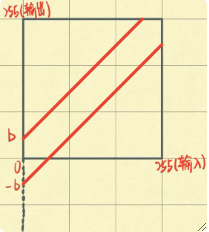
· 水平镜像计算公式:
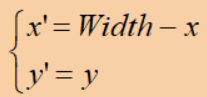
· 矩阵表达为:
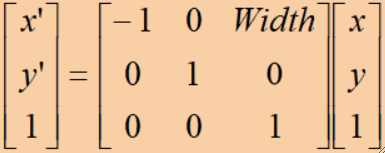
· 垂直镜像计算公式:
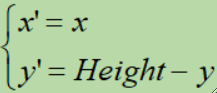
· 矩阵表达为:
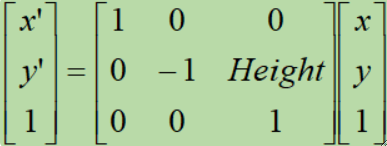
· 值得注意的是,上述公式都是以穿过原点的X轴为对称轴的,如果要实现对任意轴进行镜像变换,则需要进行级联操作,具体如下:
先把轴平移距离d使其与原点相交 -> 让轴旋转α度使其与X轴重合 -> 作垂直镜像 -> 把结果图像旋转-α度 -> 把结果图像平移-d距离
· 镜像变换例子:

转置变换
· 转置就是将图像的x坐标与y坐标互换,该操作会改变图像的大小,但输入与输出仍是一一对应的,不需要插值计算。
· 公式矩阵表达如下:
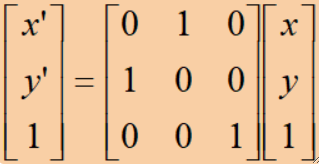
· 例子:

缩放变换
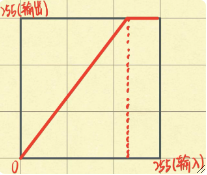
· 缩放操作会改变图像的大小,同时因为输出图像可能在输入图像中找不到对应像素点,因此需要进行插值操作。
· 公式为:
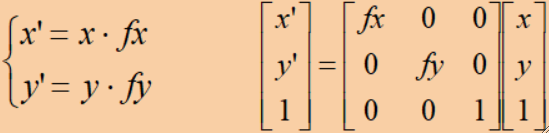
· 其逆运算为:
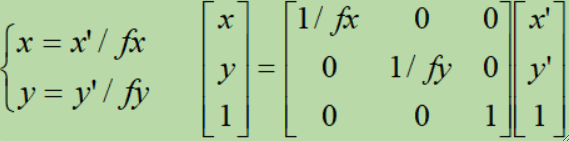
· 注意,上述公式的参考点选择的是坐标系的原点而不是图像中心!如果要实现以图像中心缩放,则需要先把图像中心移到原点-> 缩放 -> 移回去三步,这包含了平移、缩放、平移三个矩阵,把这三个矩阵乘在一起,即可得到一个最后的目标矩阵。
旋转变化
· 该操作会改变图像的大小,因此也需要进行插值操作。
· 首先,我们通过以下公式,即可使用旋转的角度获取旋转后点的坐标:
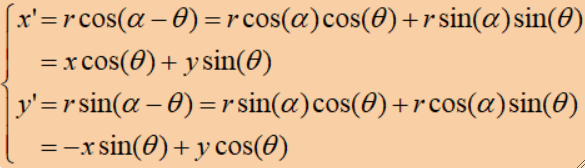
· 写成矩阵表达的形式为:
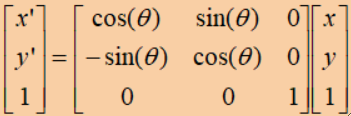
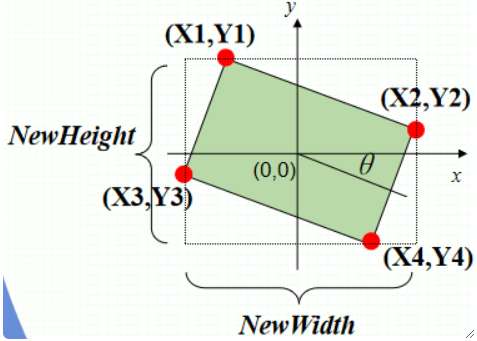
· 设图像的宽高为Width和Height,以图像中心为原点,则可计算出旋转前四个顶点的坐标:
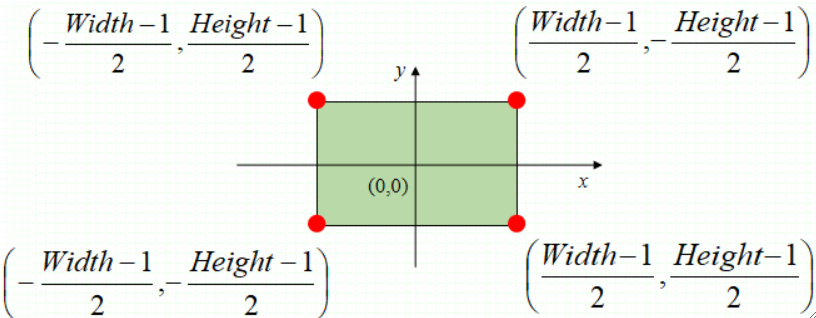
· 按照旋转的公式,可计算出旋转后四个定点的坐标:
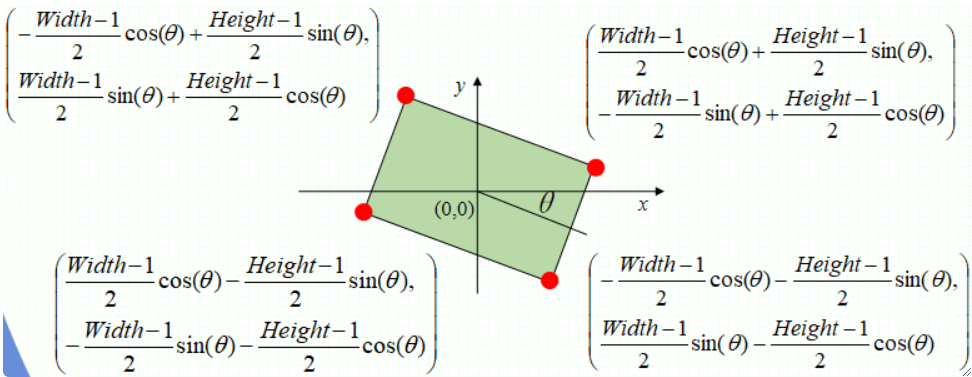
· 然后我们需要计算新的图像的宽高:
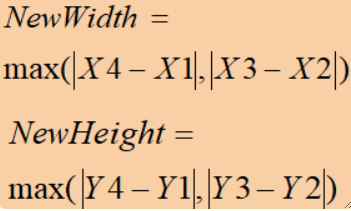
· 最后:
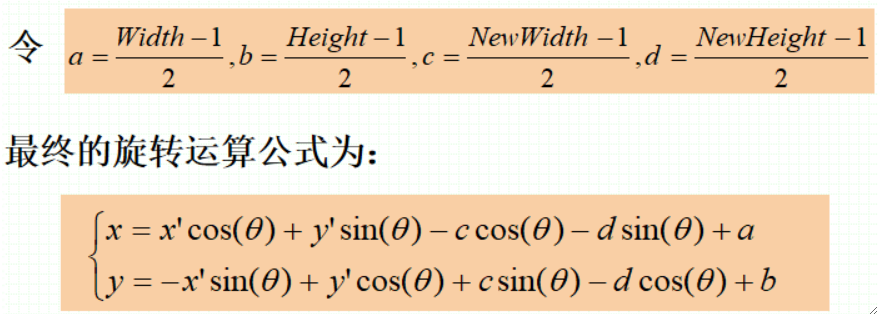
插值算法
· 我们刚刚提到的缩放、旋转操作,可能在原图中找不到相应的像素点,这样就需要通过插值算法来计算:
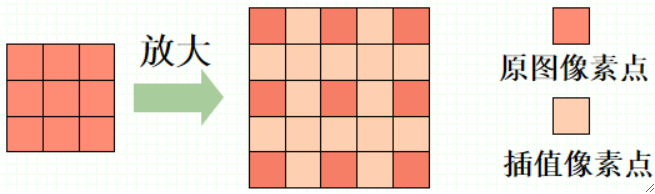
· 插值算法①——最邻近插值(0阶插值)
· 是最简单的插值方法,顾名思义,令输出图像的灰度值等于离它所映射到的位置最近的输入像素的灰度值。
· 优点是算法简单,缺点也很明显,只考虑最邻近的像素,没考虑周围其它像素,这样会容易产生割裂感(锯齿)。
· 插值算法②——双线性插值(1阶插值)
· 能够产生比零阶插值更令人满意的效果。
· 我们通过一个例子来计算双线性插值,已知(0,0),(0,1),(1,0),(1,1)四个点以及其对应的像素值f,求点(x,y)的像素值:
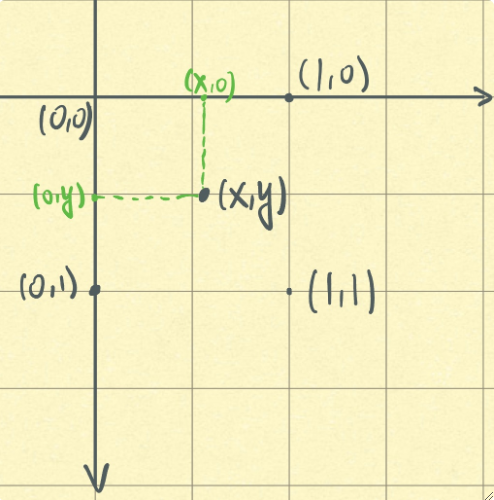
· 按照以下步骤计算即可,其实本质上就是计算一个占比。
① 计算f(x,0)的值,可以理解为f(1,0)到f(0,0)的差值,占x份。
② 计算f(x,1)的值,同上。
③ 计算f(x,y)的值,可以理解为f(x,1)到f(x,0)的差值,占y份。
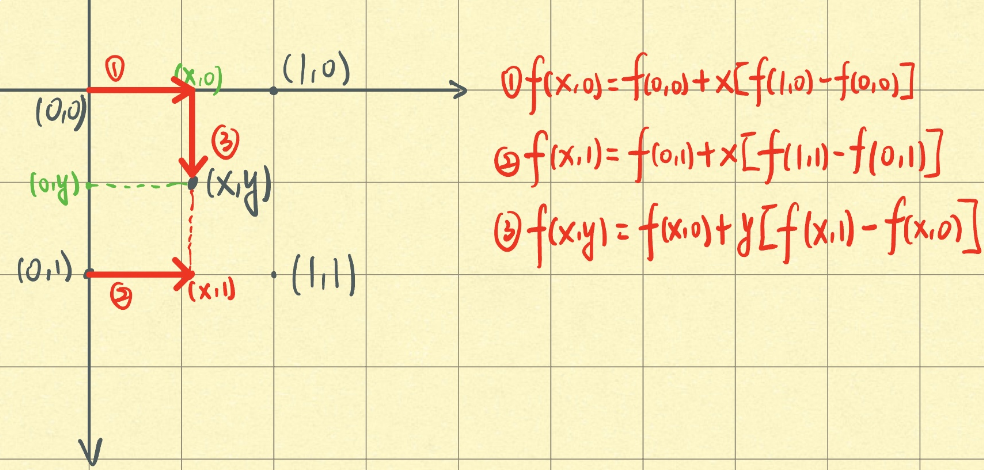
· 我们来算一个具体的例子,已知f(0,0)=100,f(1,0)=150,f(0,1)=50,f(1,1)=160,求f(0.2,0,7)。
① f(0.2, 0)=100+0.2*(150-100)=110
② f(0.2, 1)=50+0.2*(160-50)=72
③ f(0.2, 0,7)=110+0.7*(72-110)=83.4
· 插值算法③——高阶插值
· 高阶插值,优点是能得到更好的效果,缺点是计算量大大增加。
灰度直方图
· 常见的直方图有两种,灰度直方图和彩色图像的分通道直方图:
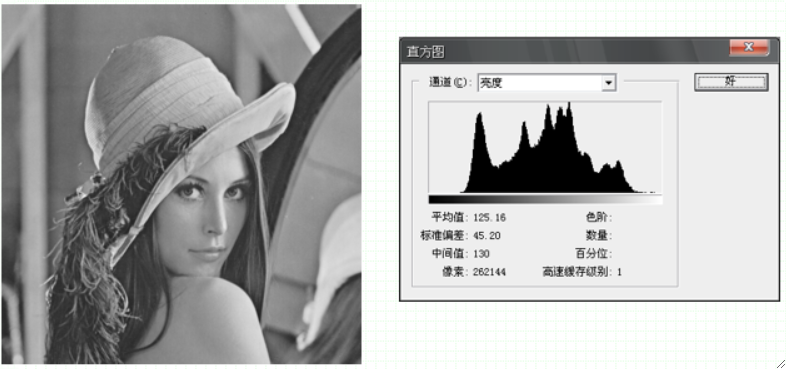
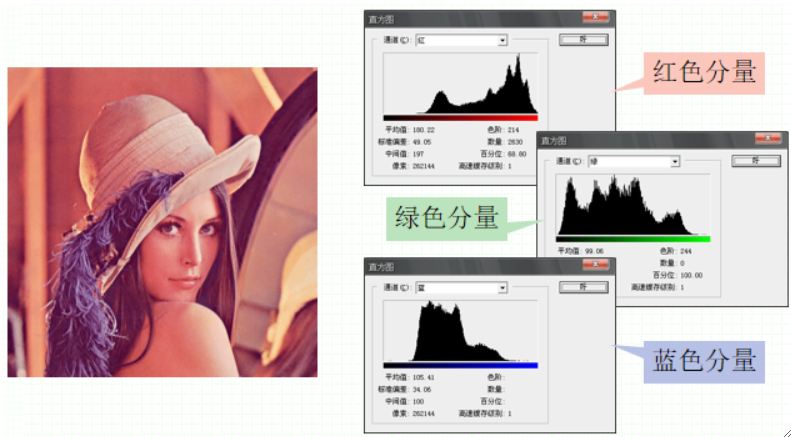
· 灰度直方图用于描述图像中具有该灰度级的像素的个数,其横坐标是灰度级,纵坐标是该灰度出现的概率。
· 计算灰度直方图的步骤如下:
① 首先确定图像的灰度级L,通常L=256,即8位灰度级。
② 初始化一个数组H,H[k]=0,k为0到L-1。
③ 遍历每一个像素点,获取其灰度值,并给对应的H自增1,即H[f(x,y)]++,其中xy为图像宽高。
④ 最后归一化,把对应的H中的值转换为概率,即H[f(x,y)] /= M*N,其中MN为宽高。
· 灰度直方图具有以下几点性质:
① 不表示图像的空间信息,它只能告诉你每个灰度级的像素个数,具体像素位置不能得到。
② 任一特定图像都有唯一直方图,但一个直方图可能对应多个图像,例如在图像中移动物体不会改变直方图,但是是两幅图像。
③ 直方图具有可相加性,若一个图像由两个不连接的区域组成,并且每个区域的直方图已知,则整张图像的直方图是该两个区域的直方图之和。
· 灰度直方图有非常多的作用,接下来详细介绍它的作用。
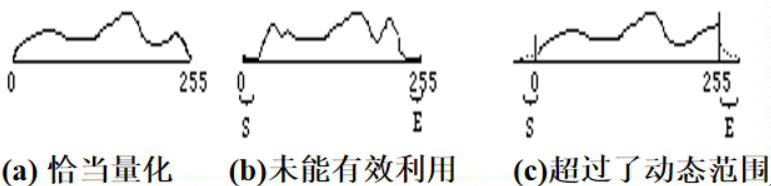
判断量化是否恰当
· 直方图一眼看上去就可以看出是否合理利用了全部被允许的灰度级范围。
· 理想状态下,高质量的数字图像应该利用全部或几乎全部可能的灰度级。
判断图像的影调(明暗/曝光)
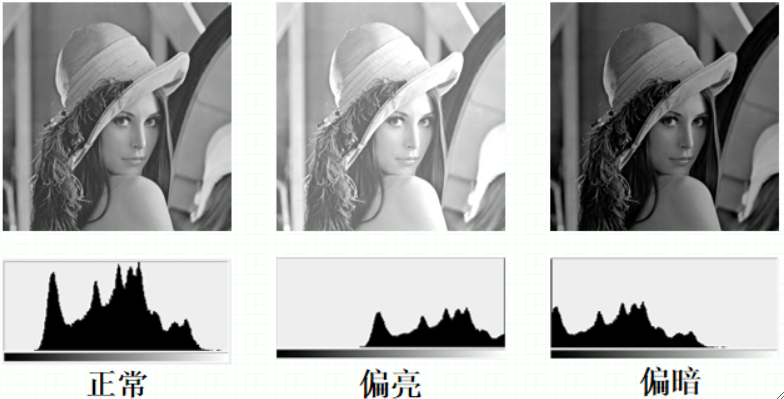
· 比较正常的图像的直方图应该分布比较均匀,如果整体偏右则偏亮,偏左则偏暗。
判断图像的对比度
· 对比度指的是一幅图像中灰度反差的大小,反差越大对比度越高。

边界阈值选择
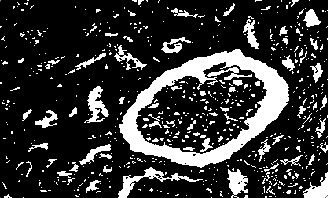
· 首先我们来看下面这张图,如果我们需要把这个细胞的边界特征提取出来,就需要先把这张图转为二值图像。
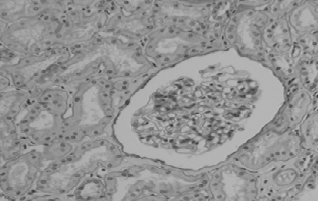
· 要把它转为二值图像,我们就需要设定一个阈值,灰度低于该阈值就设为0,否则设为1。
· 使用灰度图就能很好的选择这个阈值,我们来看这张图的灰度直方图:
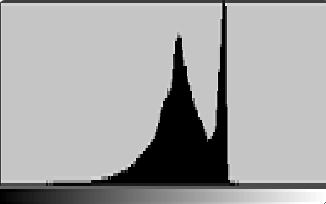
· 可以看到,有两个峰,左峰是由偏黑的像素点产生的,右峰是由偏白的像素点产生的,那中间的低谷处的值就可以作为阈值。
· 我们设定这个阈值为T,然后遍历原图的像素点重新设置即可:
特殊风格
· 通过直方图还能调出特殊风格的图片:
点运算
· 对于点运算,输出图像的每个像素点的灰度值由输入图像的像素点决定,将改变一幅图像的灰度直方图。
· 若输入图像为A,输出图像为B,则点运算可表示为:
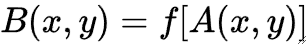
· 点运算又被称为对比度增强、拉伸或曲线变换。
· 点运算有以下两个特点:
① 输入像素与输出像素一一对应。
② 不改变图像的空间关系。
· 接下来将详细介绍点运算的各种种类。
线性运算
· 函数f(D)为线性函数,它的形式如下:
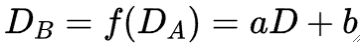
· 公式中,DA为输入点的灰度值,DB为相应输出点的灰度值。
· a和b的变化会影响输出:
非线性运算
· 函数f(D)是一个非线性函数,它的形式如下:
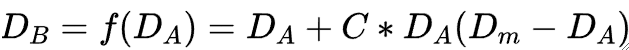
· 其中D_B为输入点的灰度值,D_M为相应输出点的灰度值;为灰度级的最大值,参数C定义了中间灰度范围内的增加(C>0)或减少(C<0)的程度。
· 如下面的函数只增加中间范围像素的灰度级,从而只使中间像素增大而两端暗亮像素变化较小。
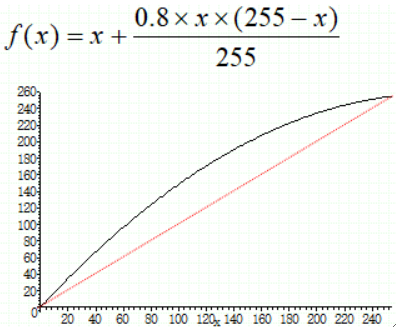
· 上面的函数的例子:

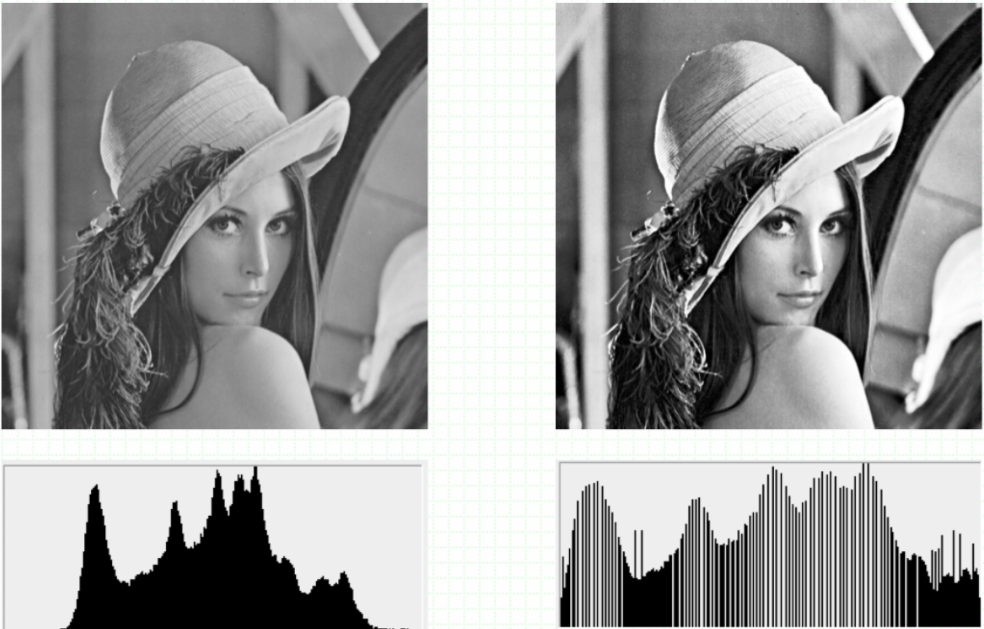
直方图均衡化
· 直方图均衡化是一个很重要的点运算。
· 目的:是把输入的图像转换为任一灰度级上都有相同的像素点数,即直方图变为平的。
· 功效:自动增加像素的灰度级分布范围,达到整个图像对比度增强的效果。
· 应用:
① 增加图像主观质量。
② 均衡化后的直方图对二值化阈值选取很有利。
③ 有利于进行传统算法,进行基于直方图的图像匹配。
· 直方图均衡化的例子:
· 直方图均衡化的公式,即累积分布函数,计算方式如下:
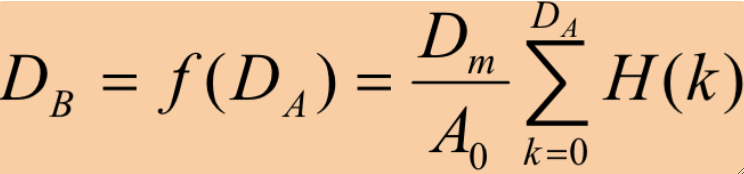
· 其中D_A是输入点的灰度值,D_B为相应输出点的灰度值,D_M是灰度级的最大值,通常为255或7,A_0是图像的面积,H[k]是输入灰度直方图。
· 下面为直方图均衡化的计算步骤,务必保证每一步都计算正确:
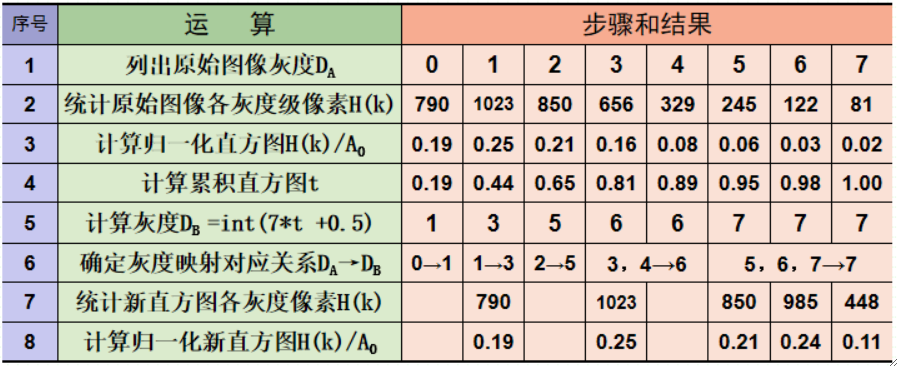
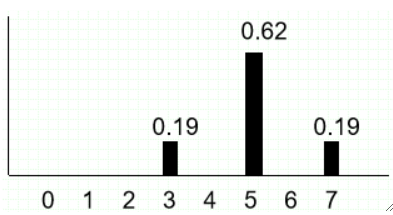
· 上方图表对应的直方图如下,首先这是原始直方图
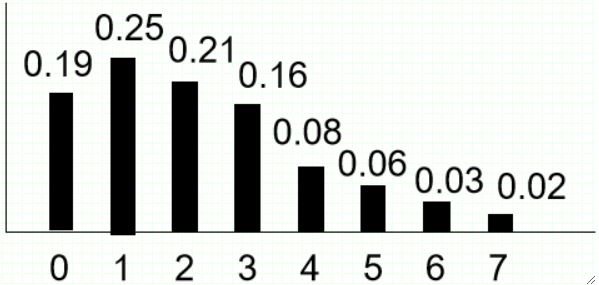
· 然后我们计算出累积直方图如下:
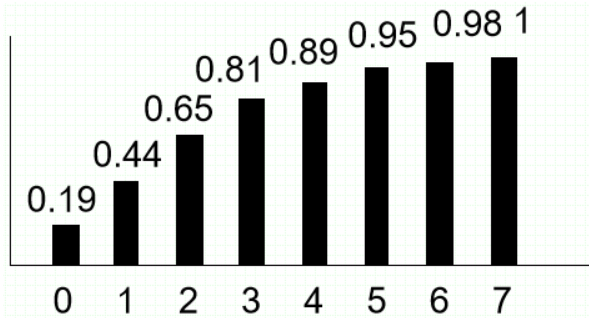
· 然后我们算出灰度值为1、3、5、6、7,以及其对应的占比即可画出均衡化直方图:
直方图规定化
· 目的:把直方图变为某个需要的形状。
· 作用:比均衡化更灵活,常用于图片风格一致性的自动处理。
· 应用:图像增强处理,保证不同图像的影调风格的一致性,在处理艺术图像时有用。
· 例子:

· 接下来简单介绍规定化的原理。
· 首先直接变化的话会比较难,但我们刚刚已经学会均衡化了,因此,我们可以先把原始直方图均衡化:
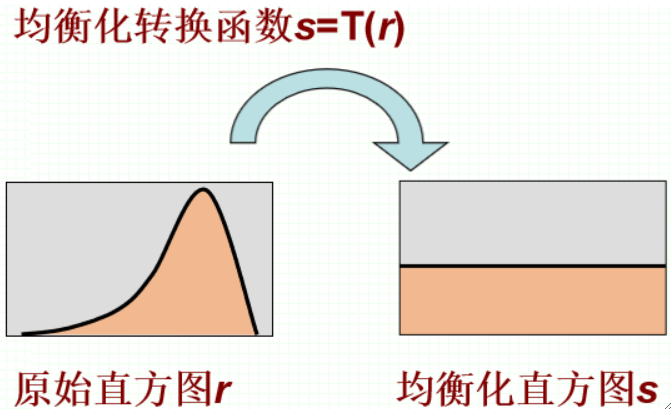
· 然后,我们可以把规定的直方图均衡化,也很简单:
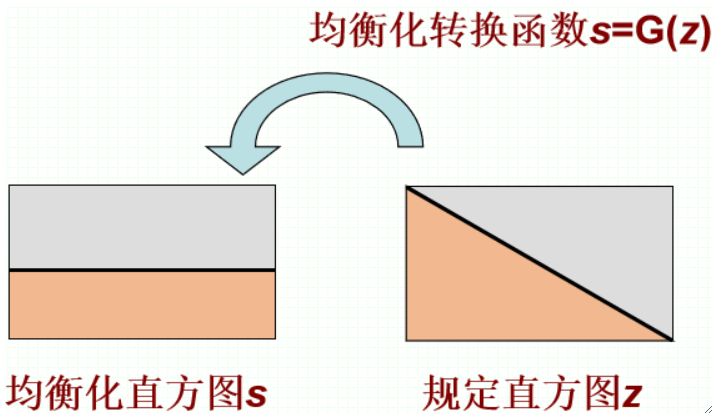
· 然后我们把G(Z)函数求反函数,即可得到均衡化到规定化的函数:
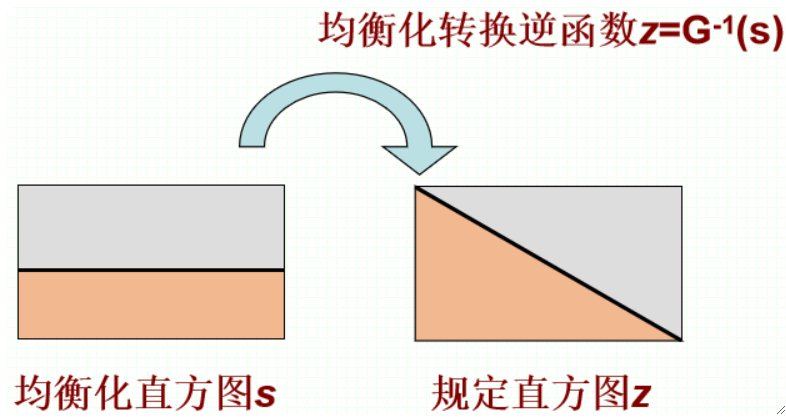
· 然后我们就得到了想要的规定化函数了:
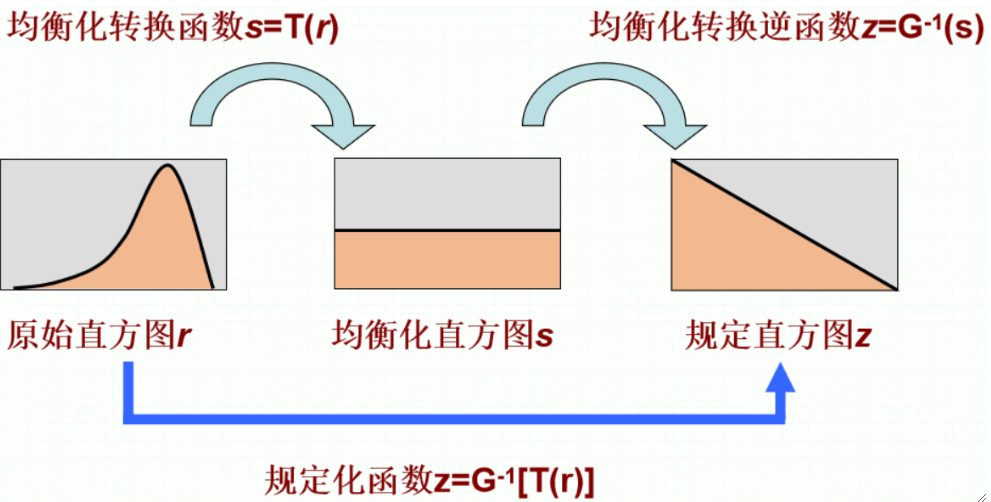
· 规定化有单映射(SML)和组映射(GML)两种实现方式。
· 首先,给出原始直方图和规定直方图:
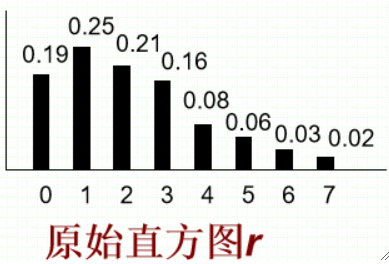
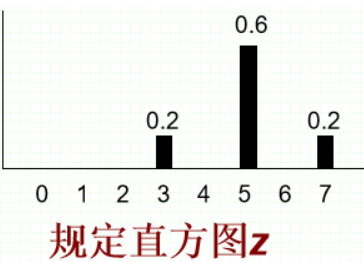
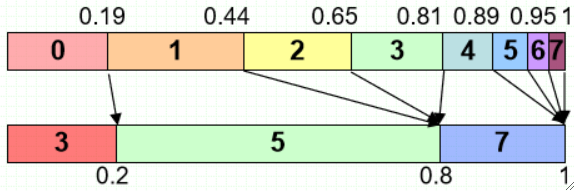
· 使用单映射其实就是把原来直方图映射到离自己最近的点去,如:
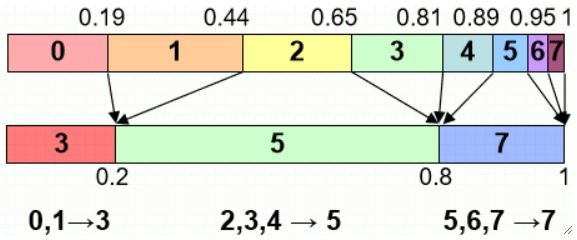
比如原来的1,离映射的3的距离是【0.44-0.2=0.24】,离映射的5的距离是【0.8-0.44=0.36】,因此选择最近的3。
比如原来的2,离映射的3的距离是【0.65-0.2=0.45】,离映射的5的距离是【0.8-0.65=0.15】,因此选择最近的5。
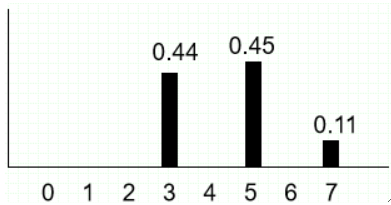
· 最后看到SML映射规定化的结果为:
· 使用组映射就比较复杂一些,但本质上是对原来的直方图进行分组。
· 首先,先对每个原直方图的点找最近的映射的点:
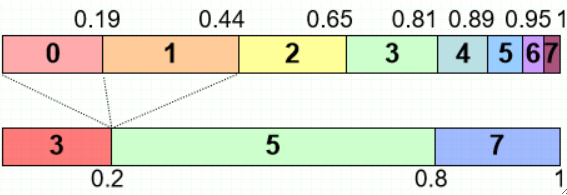
如上图,三条线所在的点映射的3最近,于是归到3这一类。
· 然后在分好的组内找最近的一点,做映射:
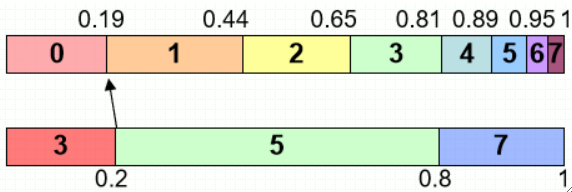
如上图,在刚刚分到的三条线内很明显中间那条最近。
· 对剩余的原直方图元素都做分组和映射处理后能得到:
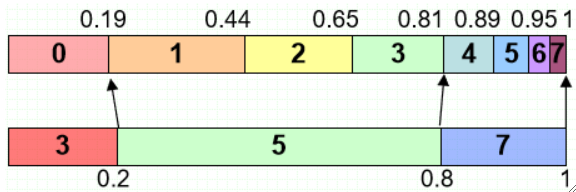
· 然后做一次反向映射,即可完成组映射的分组工作:
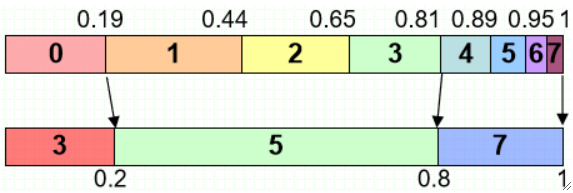
· 然后把其余的归到对应的组内即可:
· 最后可以看到GML映射规定画的结果为: