梯度下降的问题
· 复习一下,梯度下降虽然是一个很优秀的算法,但还是存在非常多的问题。
① 会卡在局部最优处,比如鞍点(Saddle Point),平原(Plateau),这和初始化点有很大的关系。
② 因为不同方向上的偏导的大小不同而造成尺度不一,学习率很难调控。
· 接下来我们介绍一些能解决这两个问题的梯度下降算法。
· 但需要注意的是,没有一个方法是能完美解决所有问题的。
动量梯度下降 GD with Momentum
· 第一个算法是动量梯度下降(Gradient Descent with Momentum,GDM)。
· 普通的梯度下降是用前一个的梯度减去当前的偏导得到的,而在GDM里,不是减去当前的偏导,而是减去动量:
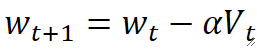
· 这个动量其实是考虑了上一次更新的动量与这一次的偏导得出的:
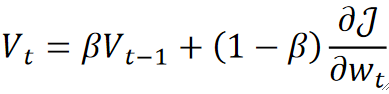
· 可以看到,在式子里我们使用了一个新的超参数\beta来控制二者的占比(调参的难度又上升了呢)。
· 一般来说超参数\beta我们都取0.9,初始动量V_0取0。
· 该算法通过模拟物理学中的动量,可以帮助我们解决局部最优的问题,但这也不是一定的,也是需要运气成分。
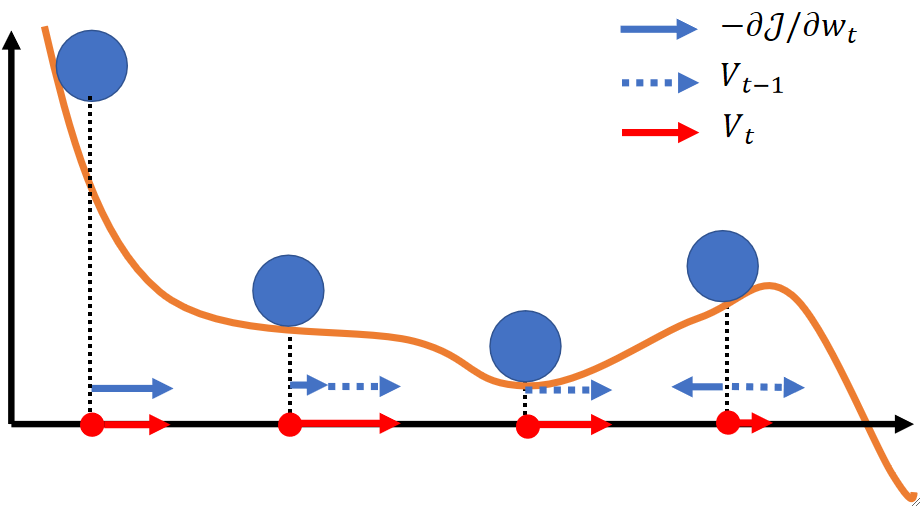
· 我们来模拟计算一下在进行几次梯度下降之后的结果:
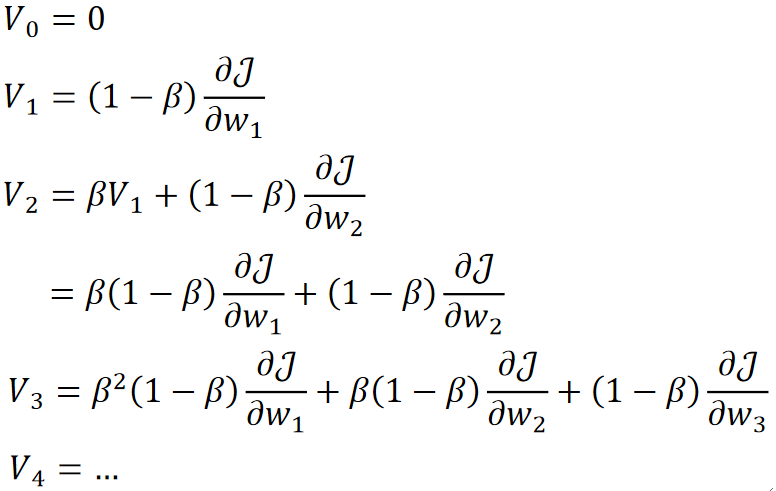
· 可以发现,随着越来越往后,V_1对当前时刻都偏导越来越小,即之前对现在的影响会越来越小!
· 其实动量更新的公式,在统计学内有一个专业的名字——指数滑动平均(Exponential Moving Average)。
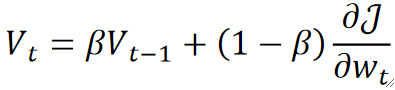
自适应梯度 Adaptive Gradient
· 第二个算法是自适应梯度(Adaptive Gradient,AdaGrad)。
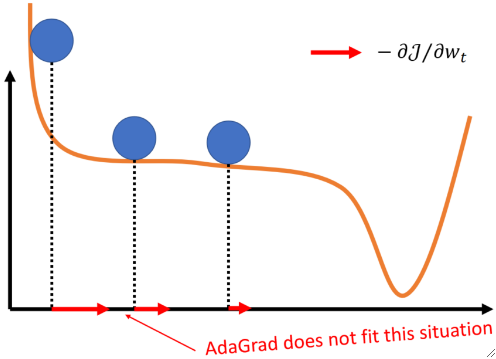
· 梯度下降的第二个问题就是尺度不均衡,而AdaGrad就可以用来解决尺度不均衡的问题。
· 聪明的小朋友就会问了,既然x,y上的尺度不一样,那我分别用两个α来控制不就好了吗?雀食,你说得对,这个思路没问题。但是如今深度学习的参数上亿,不可能每来一个模型就再加一个需要手动调的参数,这样调参就实在是太痛苦了。
· 因此我们就希望超参数也能够自己学习,因此就发明了自适应梯度。
· 梯度的更新公式和原来的很像,只是学习率做了更改:
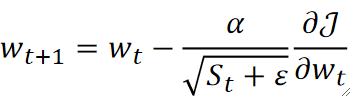
· 其中,S_t的更新公式如下:
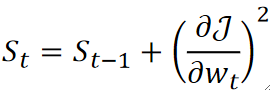
· 可以看到,S_t是作为分母存在的,意味着S_t越大,那最终的学习率就会越小,而S_t则是根据上一次的梯度来进行计算的,上一次的梯度越大,那S_t就越大,这次的W_{t+1}就越小,从而达到了动态控制学习率的效果!
· 值得注意的是,分母上S_t后面还加了个\varepsilon,这是一个超参数,但不是一个特别重S_t要的超参数,它主要是为了防止S_t过小,无限接近0而导致除零错误,一般这个参数我们都设置为10^{-7}。
· 但是这个方法有一个很明显的缺点,这个S_t会一直加一直加下去,这样后面更新的梯度就会越来越小,这不是我们所希望的。
· 解决这个问题的方法也非常简单,和刚刚一样,引入指数滑动平均即可,这样就引出了下一个优化方法。
均方根传播 RMSProp
· 这个方法被称为均方根传播(Root Mean Square Propagation,RMSProp)。
· 它其实就是在AdaGrad的基础上加入了指数滑动平均:
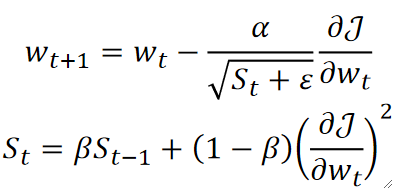
· 可以发现,\omega的更新还是一样的,只是S_t的更新方式不同,引入了一个超参数\beta来控制之前对本次的影响。
自适应矩预计 Adaptive Moment Estimation
· 最后的就是大名鼎鼎的Adam算法了,即自适应矩估计(Adaptive Moment Estimation,Adam)。
· 其实本质上,它就是GDM和RMSProp的结合。
· 首先我们使用GDM来引入一个\widehat{V_t} :
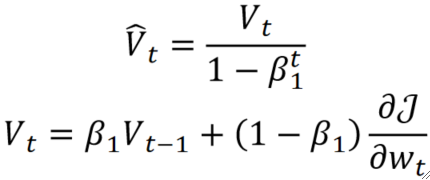
· 其中\beta_1是引入的超参数,用于控制\widehat{V_t} 的重要程度。
· 然后我们使用RMSProp来引入一个\widehat{S_t} :
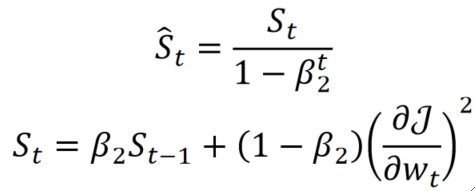
· 其中\beta_2是引入的超参数,用于控制\widehat{S_t} 的重要程度。
· 然后我们把\widehat{Vt} 和\widehat{S_t} 揉在一起:
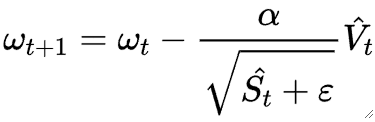
· 通常来说,\epsilon = 10^{-6},\beta_1=0.9,\beta_2=0.999。
· 这个时候又有聪明的小朋友要问了,为什么不直接使用V_t和S_t而是要对它们做一个处理呢?
· 首先我们来看V_t,回忆一下GDM,不难发现,一开始因为1-β是0.1,特别小,因此动量被浪费了,而需要走个十几次左右,动量才逐渐大起来,因此在Adam中,V_t就除了一下1-\beta^t,那这样子V_t就被放大了,这样前面浪费的就被补回来了。但随着越来越往后,因为有t次方的存在,所以之前的影响还是会越来越小,最终几乎为0了,这并没有变。
· 现在再来看S_t也是一样的了,我们的\beta_2一开始是0.999,那就更夸张了,前面浪费的就更多了,因此用同样的方法来把前面失去的偏导补回来。
一些其它的梯度下降算法
· 接下来介绍一些行业内的其它梯度下降算法。
· 首先,我们一直使用的,考虑所有样本的梯度下降被称为批量梯度下降(Batch GD)。
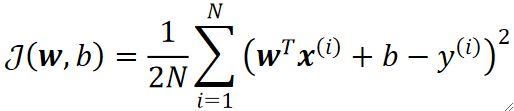
· 接下来介绍随机梯度下降(Stochastic GD),它的核心思想是每次只任意挑一个样本的LOSS作为总的代价,但每次挑的样本都不一样。
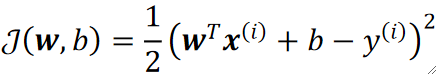
· 但其实因为每次挑的样本都不一样,那本质上也是把所有样本都试了一遍,因此最终的效果还是很不错的。而且每走完一轮之后还会接着重新走。
· 当算法每走完一轮之后,我们称之为完成了一轮纪元(Epoch)。
· 接下来介绍小批量梯度下降(Mini-batch GD),即上面两种的折中,每次只取一部分的样本的LOSS来作为总的代价。
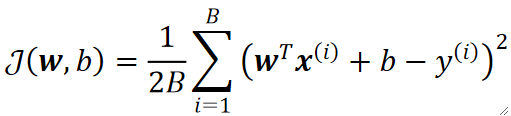
· 其中参数B代表的就是每一批的样本数量(Batch Size),这也是一个超参数,又要调参力。
· 需要注意的是,虽然小批量和随机梯度下降能极大的加快训练速度,但是因为样本数量的减少,而导致每次计算的时候最优点都会产生偏差,因为每次取的样本不一样。但其实这个问题也不大,虽然走的过程歪歪扭扭,但是总的来说还是朝着正确的方向前进的。最后虽然精度降低,但是我们获得了速度,降低了内存使用。
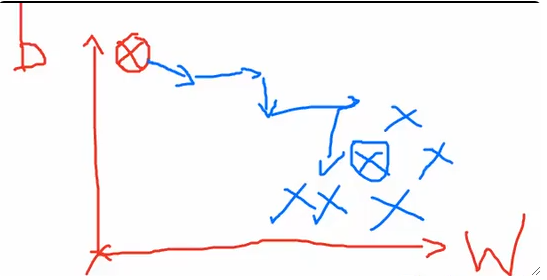
· 补充一个小问题,假设我们总共有12个样本,但是batch size设置为5,那最后多出来的两个我们一般会丢弃,或修改batch size以更多的使用样本,因为数据集的收集很昂贵。
· 现在深度学习大部分都会使用Mini-batch。
