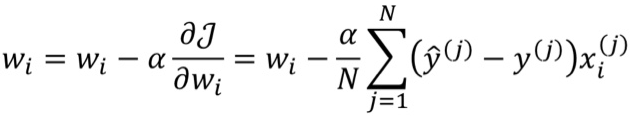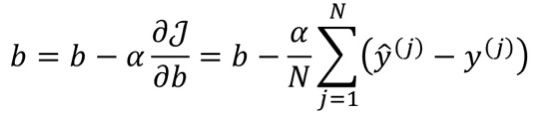分类(Classification)
· 首先需要明确的是,逻辑回归是一个分类算法。
· 分类有两种,二元分类(Binary Classification)顾名思义就是只有两个种类,多元分类(Multiclass Classification)即最终会有很多种类别,三种或以上。逻辑回归就是一个二元分类算法。
· 我们选用线性函数来进行分类任务。
从"与问题"看逻辑回归
· 我们从最简单的与问题(AND Problem)来看逻辑回归,数据集如下
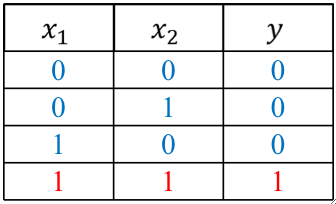
· 可以画出特征空间的图如下
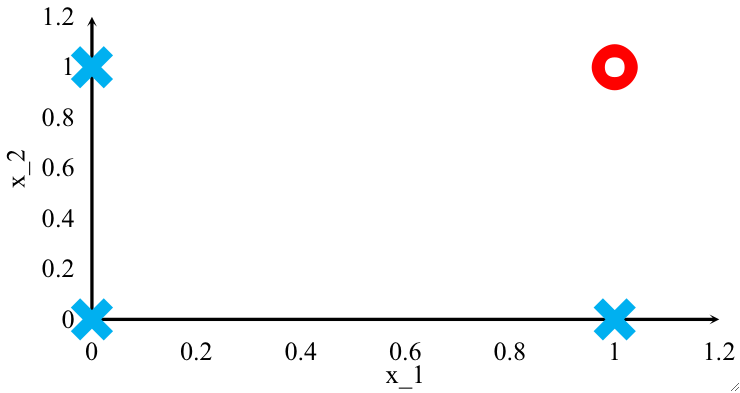
· 可以发现,和线性回归非常相似,最大的不同,就是线性回归的y值是连续的,而逻辑回归的y值是离散的,如这个例子中y值不是0就是1。
· 接下来就是选择一个模型,我们选择使用线性模型去进行分类,那就是:
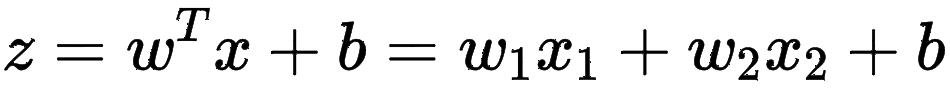
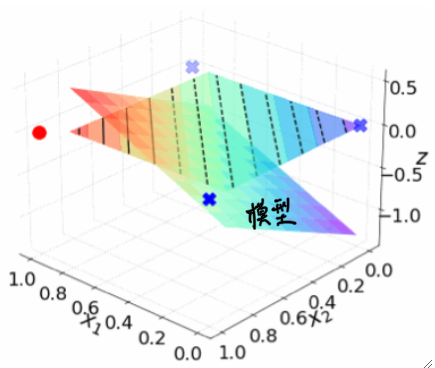
· 最终得到的结果应该是一个平面,学习的就是w1和w2和b这三个参数:
· 展示在x1-x2平面上就是一条直线:
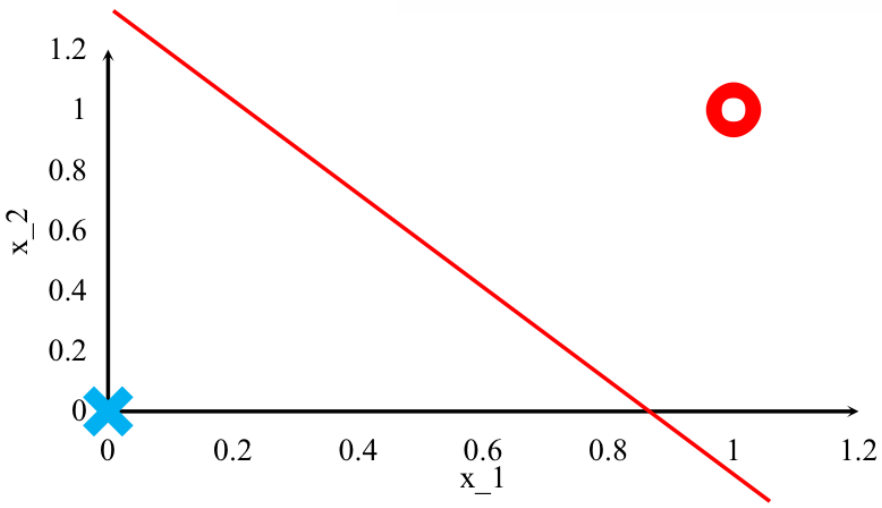
· 值得注意的是,我们对线的斜率并不敏感,即我们只关心能否分成两类,至于如何分,我们并不关心!
激活函数
· 我们刚刚的模型得到的是z并不是y hat,这是因为我们还要引入一个激活函数才能得到y hat。
· 这是因为z算出来的值理论上的取值范围是R,很明显这不是我们想要的,我们想要的不是0就是1,因此,需要引入一个函数,把z值输入,输出的值能控制在[0,1],那就方便我们转换。
· 在这里我们介绍一个Sigmoid Function,它的作用就是输入一个z,输出一个y hat,它在我们后续学习神经网络会经常用到。
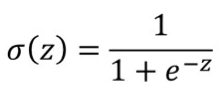
· 把它的z-y hat图画出来是这样的:
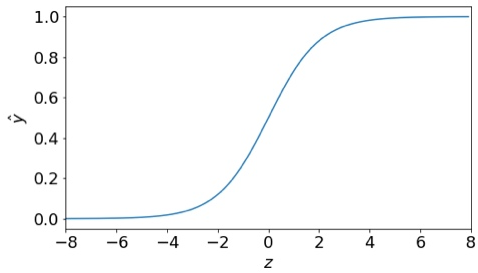
· 他的形状很像一个S,然后恰好在z=0,y hat=0.5这条线上被分为两半;除此之外,如果求这条曲线的斜率,会发现在z>4和z<-4的区间内,它的斜率就变得非常小,几乎是平的了。
· 经过了这个Sigmoid函数之后,我们得到的就是想要的y hat值了:
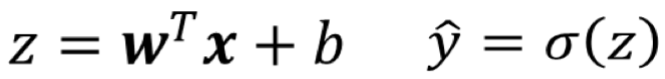
交叉熵损失函数
· 有了模型,剩下的就是损失函数了,这里,我们使用大名鼎鼎的交叉熵损失函数(Cross- entropy Loss)。
· 这个损失函数是专门用来做分类任务的损失函数的,在逻辑回归中,我们只有两类,因此我们不需要使用完全体的交叉熵损失函数,我们使用二元交叉熵即可。
· 它长这样:
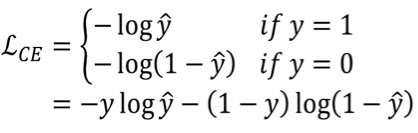
· 实际上就是分类讨论y的值,最后一条式子就是把分段函数整合到一个式子里面去了,看上去就比较优雅。
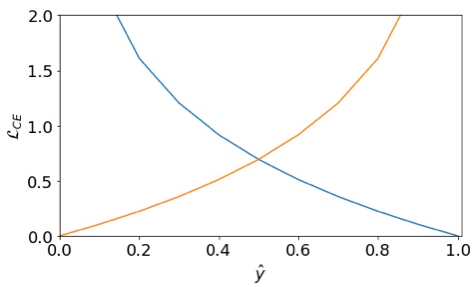
· 简单画个图就能验证这个损失函数的有效性,假如某个y为1,对应的y hat如果越接近0的话,那LOSS就会越大,越接近1的话,LOSS就会越小。
·把它的图像画出来就是这样的,其中蓝色线的y=1的情况。
梯度下降优化
· 最后一步就是优化了,我们依然使用梯度下降去优化,那我们就要先把梯度算出来。
·首先,我们把模型和损失函数列出来:
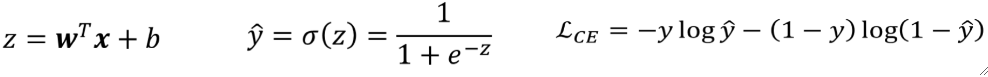
· 然后,梯度就是偏L偏w、偏L偏b:
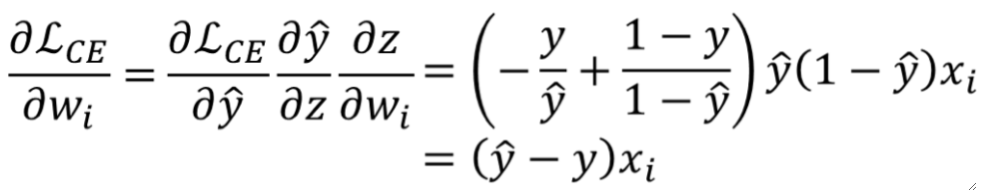
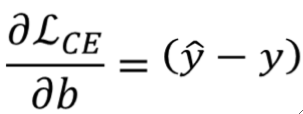
· 算出梯度之后,就可以写出代价函数了:
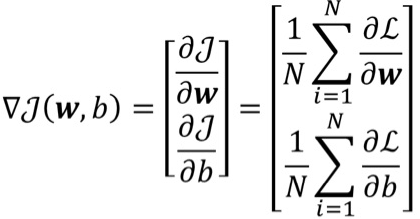
· 最后可以得到更新的公式为: