引入
· 我们知道,当模型出现过拟合的时候,可以通过两种手段来降低过拟合,一种是收集更多数据,这样模型“猜”的空间就变少了。而另一种则是正则化。
· 当然,正则化也不是万能的,它在降低过拟合的同时也会导致欠拟合,但是至少能解决一部分问题。
概述
· 首先我们来对比以下两个模型,凭感觉我们可以知道第二个模型会更加复杂:
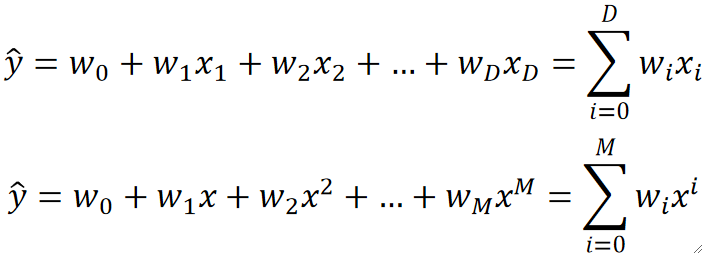
· 但肯定不能凭感觉对吧,我们需要有科学的判断依据。
· 我们可以通过参数数量与特征数量的比值来确定一个模型的复杂程度。
· 可以看到第一个模型有D个参数,D个特征,那比值就是1;而第二个模型有M个参数,但只有一个特征X,注意,它只是次数不一样而已,但仍然是同一个特征X,那比值就特别大了。
· 所以第二个模型的复杂度更高,更容易过拟合!
L2正则化
· 最常用的正则化方法是L2正则化(L2 Regularization)。
· L2正则化的正则项表达式如下:
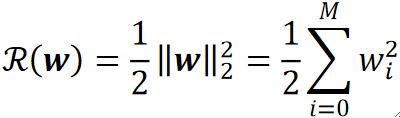
· 在式子中会发现w左右有两个竖线,并且右下标有一个2,这个符号代表的是范数,2范数代表的是求模长,在这里求的就是w向量的模长。
· 写成展开的形式其实就是对M个wi的平方求a和再乘个1/2。
· 其实这个R(w)是一个惩罚项。它用于惩罚代价函数中的模型,如果模型越复杂,那惩罚的力度就会越大。举个例子:
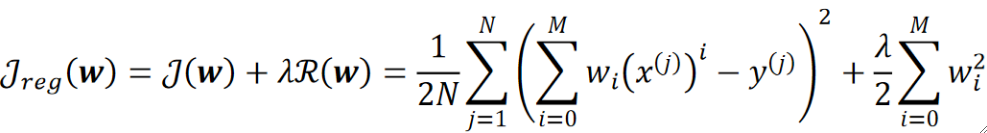
· 可以看到,在原本的代价函数J后面加入了一个L2正则项,以此为最终的代价J,模型越复杂后面的R就会越大,就会导致代价越大,模型就会继续学习,这样就能一定程度上减少过拟合。
· 从直觉上来理解就是,假设我们设定了某个模型有三个参数w0,w1,w2,但实际上只需要w0和w1即可很好的拟合函数,这样我们设定的模型就会过拟合。在这种情况下,如果模型过拟合,那代价J会比较小,但是加上正则项之后,J由于w2而变大了,那模型就不会停止学习,会继续尝试寻找更好的解,最终会学出w0和w1比较大,w2很接近0的效果,这样也能达到我们的目标函数。
· 可以看到还加入了一个超参数拉姆达,这是用来控制惩罚的力度的。
· 当拉姆达为0的时候就是忽略正则项,不对模型进行惩罚,这样模型就会保持过拟合;当拉姆达为无穷的时候,则整个模型会往最简单的去学,这样就会导致欠拟合。
· 接下来我们把图画出来看看,首先定义我们的模型是y hat=w0+w1x,因为再复杂就有点难画了,画出J和R的图像,左边是J,右边是R:
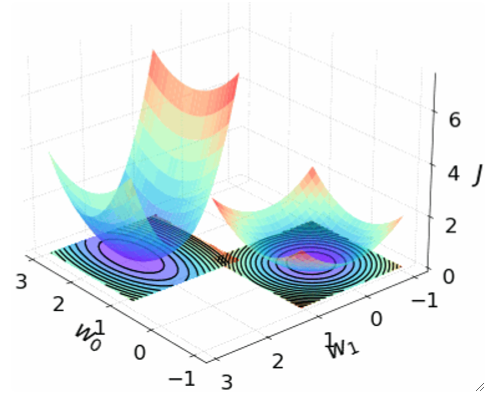
· 然后我们把这个图“拍扁”,去掉J轴,则可以看到,黑色线代表的是R,有颜色的代表的是J:
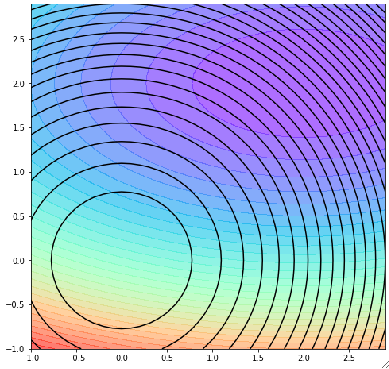
· 对于正则项R,一个圈上的R值都是一样的,但是所对应的代价值J是不一样的。
· 但是在同一个R上,肯定存在一个最小的J,这个J就是等高线上最小的值,如最里面的圆J最小的就是叉所在的点:
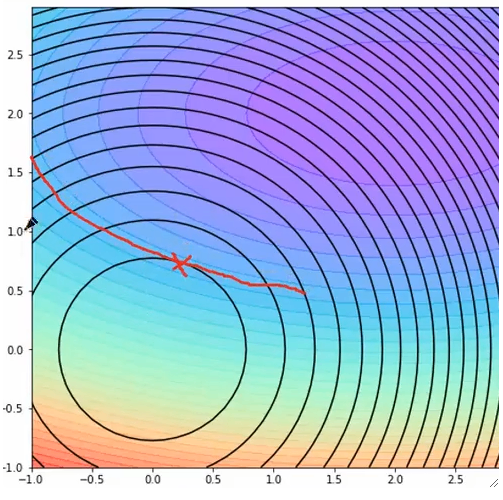
· 因此,最后模型学习出来的结果肯定在这一条线上:
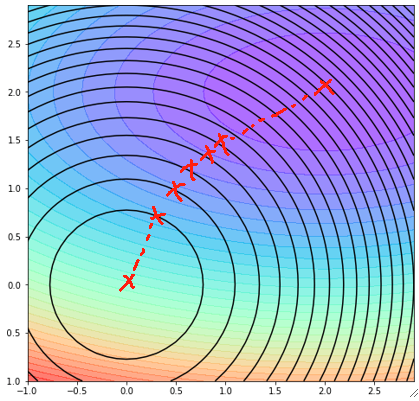
· 至此,L2正则分析完成,接下来我们来把推一下公式:

L1正则化
· L1正则是另一种常用的正则化方式,但是对比L2会比较难求导。
· 它的表达形式如下:
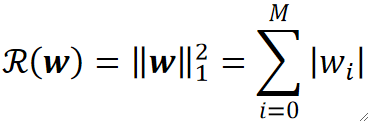
· 可以看到,范数变成1了,代表的就是求绝对值。
· 然后我们在来看看L1正则画出的图像,左边是代价J的图像,右边是L1正则的R的图像,对比L2的,变得有棱有角了:
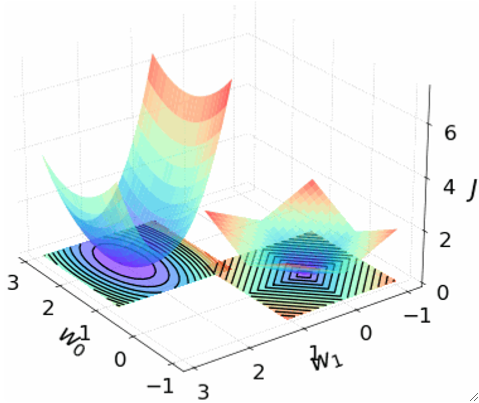
· 同样的,把J轴去掉之后的图变成了:
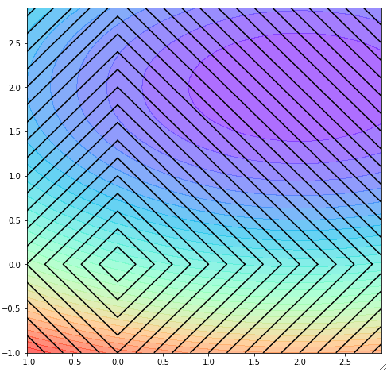
· 同样的思路,最后模型学出来的效果肯定在这条线上:
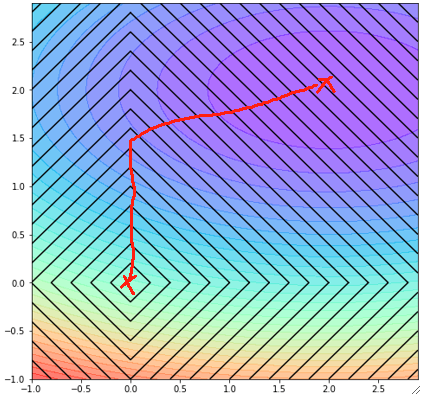
· 对比L2正则,L1正则还有另一个作用,那就是特征选择,可以看到,在橙色那一段里面,w0一直都是0,那相当于这一个特征被去掉了:
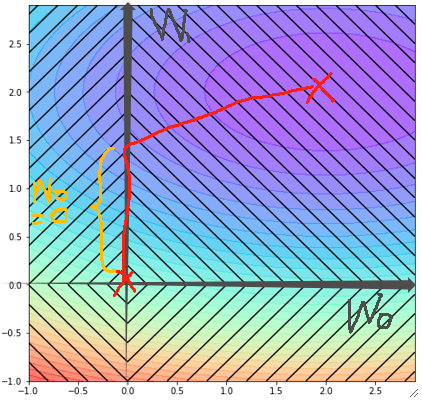
· 同样的康康L1正则的求导,其中sign是指示函数,用于绝对值求导的分段讨论:

