概述
· 我们知道,选择模型是一件非常困难的事情,调参非常的痛苦,而神经网络就可以帮我们完成这件事情。
· 神经网络的作用其实就是帮助我们优化模型,除此之外,没有改变我们在进行机器学习的时候的其它任何事情。
· 接下来,我们通过多分类,使用Softmax回归来展示神经网络。
· 我们使用的还是学习Softmax的时候的例子,两个特征,三个类别:
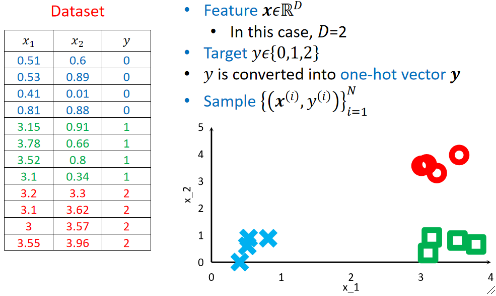
神经元 Neuron
· 首先,在进行多分类任务的时候,我们使用的模型还是一个线性模型:
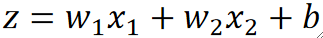
· 但是,在神经网络中,我们把模型改个名字,称为神经元(Neuron),而这种线性模型就被称为线性神经元(Linear Neuron)。
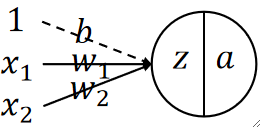
· 在神经网络中,我们可以用图像来把神经元画出来帮助我们理解:
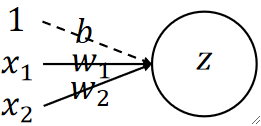
· 其中,一条线代表一个参数,圆圈z代表的是输出。
· 但是如果想更好的进行分类,那线性模型肯定是不够的,需要“把直的线掰弯”,加入非线性(Nonlinearity),因此,我们需要选择一个激活函数,此处我们选择Sigmoid函数:
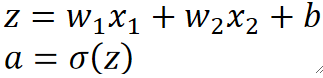
· 这样把线性神经元激活之后就是完全体的神经元了,我们这样表示:
神经网络 Neural Network
· 把神经元组合起来,就是一个完整的神经网络了:
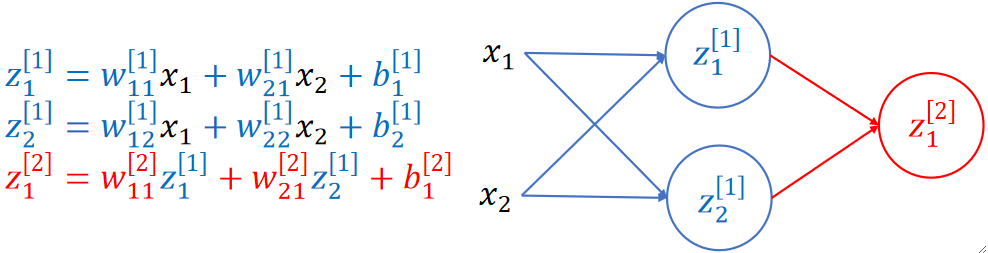
· 不难发现,其实神经网络就是一个多元复合函数,所有神经网络的本质都是多元复合函数!
· 然后我们来仔细看看这个神经网络的图,可以发现,b的箭头被省略了,箭头上也没标识参数了。
· 要看懂这个图也不难,只需要搞清楚这条线是谁通过谁得到的即可,比如下方黄色线的参数就是这么来的,注意上标中括号代表的是第几层:
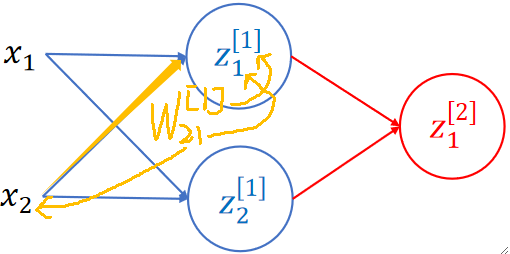
· 当然,上面的神经网络还只是一个线性神经网络,还不是完全体,需要加上激活函数才是完全体。
· 为什么线性神经网络不好?因为线性神经网络本质上还是一个单层的网络,比如我们把z1[1]和z2[1]带入z1[2]的式子里面去,实际上中间层就全部消失了,那就只是一个简单的线性函数,如果只是一个简单的线性函数,那学习能力再强也强不到哪里去:
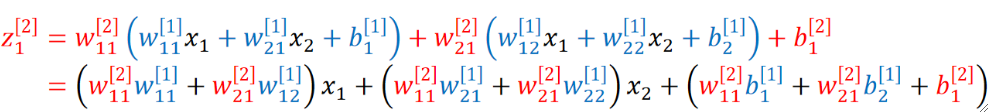
· 那么我们加上激活函数之后就是完全体的神经网络了:
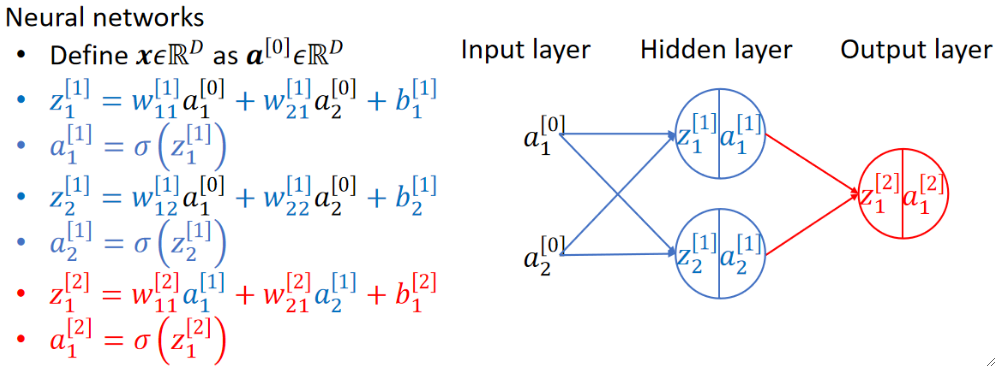
· 我们把输入的特征的一层称为输入层(Input Layer),中间所有的层称为隐藏层(Hidden Layer),最后的层称为输出层(Output Layer)。
激活函数 Activation Functions
· 常用的激活函数有以下几种:
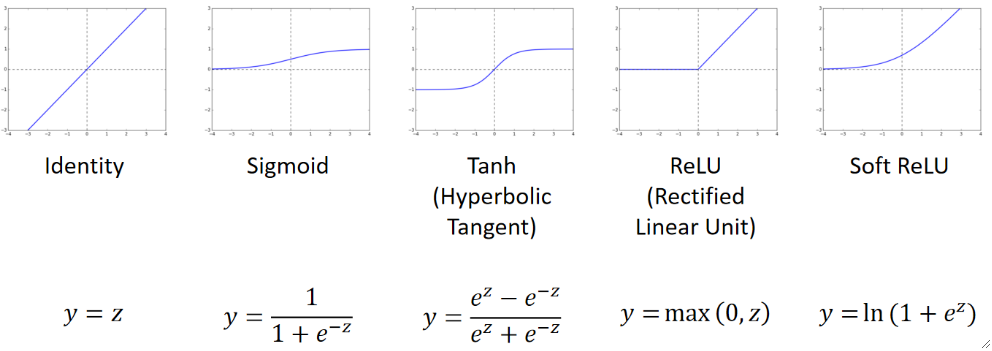
· 我们最熟悉的就是Sigmoid函数,而深度学习则大多数会使用ReLU。
· 第三个是双曲正切函数,它能把值限定在[-1,1],和Sigmoid有点类似。
· 第四个是大名鼎鼎的ReLU,它效果好的原因是,当我们对x求偏导的时候,x>=0时是1,x<0是0,在使用链式法则的时候,就会乘很多个1,对总体的梯度偏J偏w没有影响;而像Sigmoid这种,求出来的偏导比较小,那最后就会越乘越小,导致梯度消失,或者梯度爆炸,而ReLU能很好的解决这个问题。
· 第五个和ReLU很像,是ReLU的变体。
全连接神经网络 Fully Connected Neural Networks
· 有了最基础的神经网络的架构之后,我们就能把中间整个神经网络画出来了:
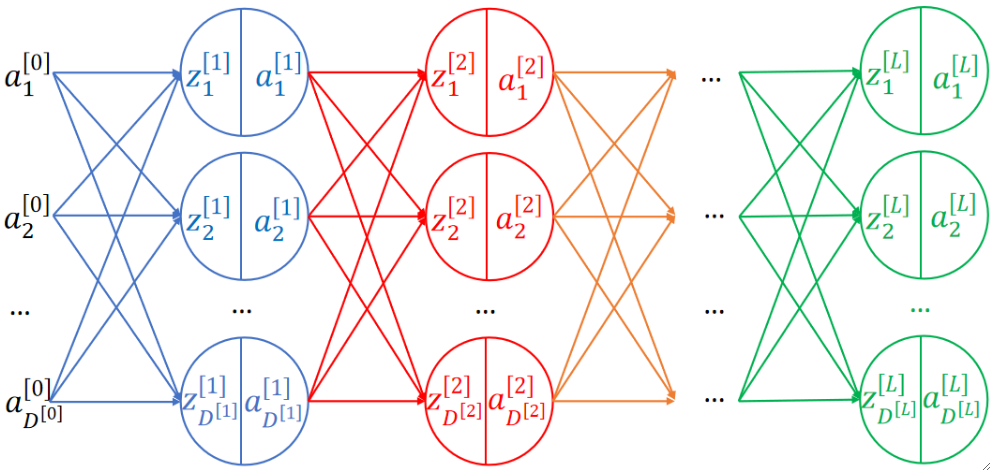
· 整个套路都是一样的。
· 我们把除了输入层和输出层外的中间全部层称为全连接层(Fully Connected Layer)。
· 其中,计算其中每一层的z和a的方法如下:
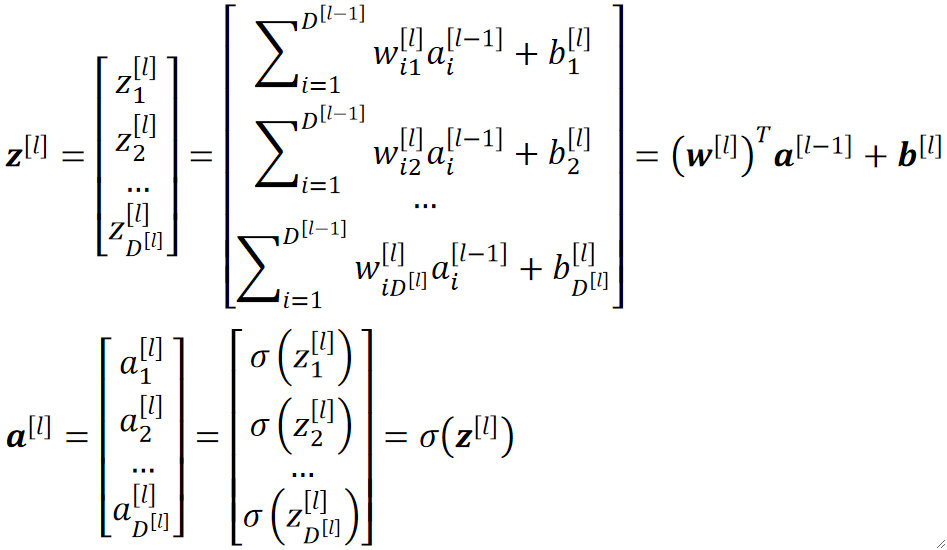
· 其实就是先算线性函数然后往激活函数Sigmoid里面一套即可。
· 最后我们的输出层就是把L-1层的a套入Softmax函数即可,本质上还是那样子运算,可以理解为只是激活函数变成了Softmax:
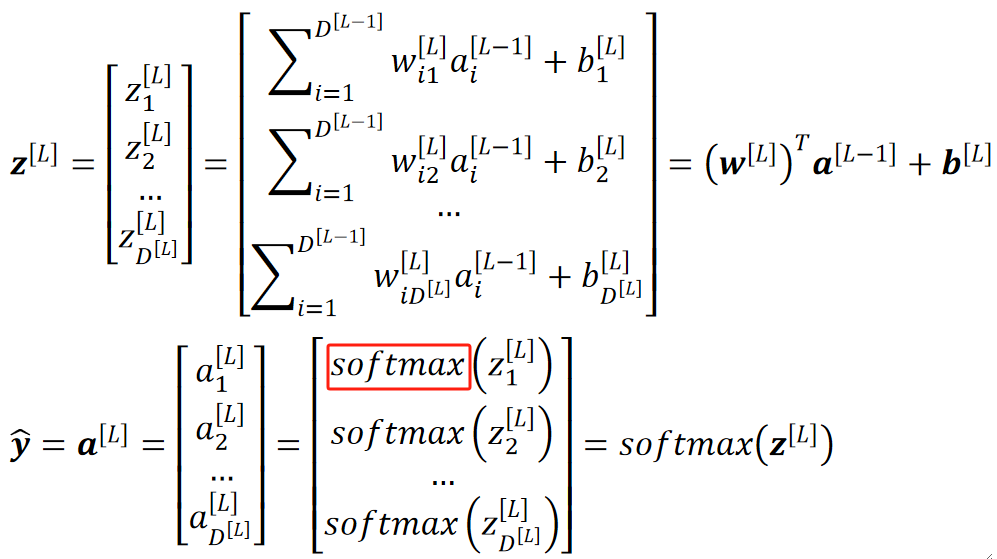
· 其实我们不难发现,从最开始我们要做分类任务,到在输出层套一个Softmax函数进行分类,其实本质上,我们的流程确实是没有变的。
· 在这个过程中,其实神经网络只是优化了我们的输入,它把输入的特征变为了一个新的特征,也就是说,神经网络自己从我们的数据中找到了规律,把这个规律提取出来以方便我们的模型更好的学习!
· 所以,神经网络本质上是一个特征提取器(Feature Extractor)!虽然我们人类无法看懂提取出来的特征是什么,但是没关系,机器可以理解即可,最后得到我们想要的效果即可。
` 就比如我们现在要做的这个多分类,原本杂乱无章混在一起的数据,经过了神经网络之后,就会变成线性可分的,这样我们的Softmax函数就能表现出更好的效果!
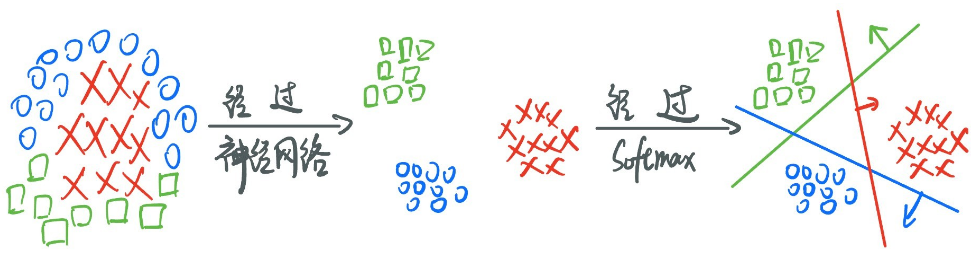
· 所以,神经网络只是一个工具,不会影响我们的任务,它可以用在我们之前学的任何回归、分类等任务。
· 比如我们做线性回归,那就把数据往神经网络里面套,最后得到的L层的a就是y hat,不需要像多分类Softmax再经过一层激活函数了。
· 最后我们来看看我们一开始的多分类任务在使用了神经网络之后的效果,可以看到非常好:
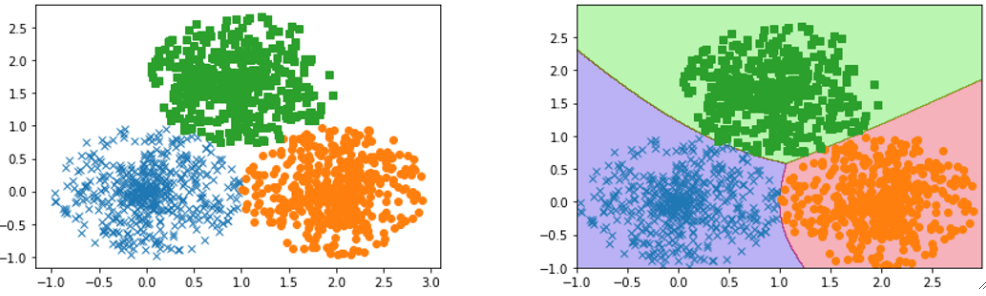
· 最终我们加上了神经网络的Softmax回归模型为:
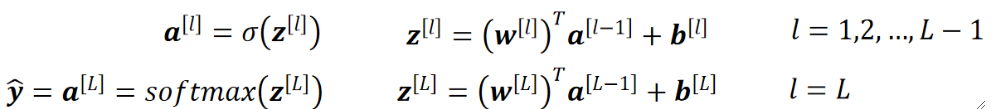
· 计算LOSS:
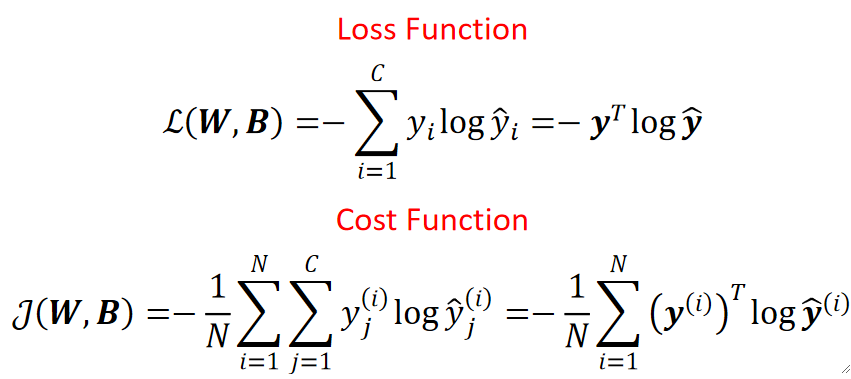
· 然后就是痛苦的梯度下降计算了。
神经网络中的梯度下降计算
· 首先我们计算输出层的梯度,这个是比较好算的,其实就是Softmax的梯度计算而已:

· 对倒数第二层求导:

· 我们会发现,前面还有很多很多层需要求,这个时候一直求下去是不现实的,因此,大名鼎鼎的反向传播(Back Propagation)出现了。
· 在学习反向传播之前,我们需要先弄清楚正向传播(Forward Propagation)是什么。
· 正向传播其实很好理解,从一开始的输入,得到第一层的输出a[l],第一层的输出a[l]作为第二层的输入a[l-1],如此循环直到最后一层。
· 而反向传播就是,从最后我们求出偏l偏z得到了L层的梯度,然后反向传播到L-1层,在L-1层求梯度的时候需要用到:

· 同理,推L-2层也是一样的:

· 之后都是一样的了,知道传播到输入层,这样所有层的参数都会被更新一次了。
· 我们来总结一下反向传播:
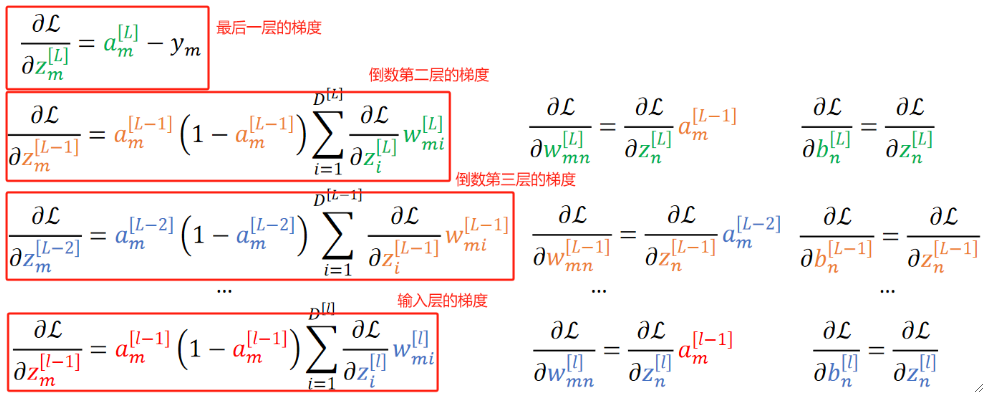
· 最后来总结一下模型:

